§ 3. Дифференцирование векторов, матриц, определителей. Комплекснозначные функции действительного аргумента
Дифференцирование векторов и матриц осуществляется по обычным правилам:
если
вектор-функция, то
если
матрица, состоящая из функций от
то
Операция дифференцирования является линейной в том смысле, что
для вектор-функций
;
для матриц
.
В обеих формулах
константы.
Аналогичным образом осуществляется интегрирование вектор-функций и матриц. А именно,
Дифференцирование
произведений векторов и матриц (скалярное,
векторное и смешанное произведение
векторов, произведение матриц, произведение
вектора на скаляр и т.д.) сохраняет
многие, но не все свойства, присущие
дифференцированию произведения обычных
функций. Так, например, если
векторы из
координаты которых зависят от переменной
и
их скалярное произведение, то
Для векторного произведения также
но в общем случае
Аналогично этому для произведения
матриц
Интересно отметить, что
а правильная формула выглядит так:
Докажем в качестве примера формулу
дифференцирования скалярного произведения
векторов. Пусть
Тогда
Дифференцирование определителя может быть выполнено на основании следующей теоремы.
Теорема.
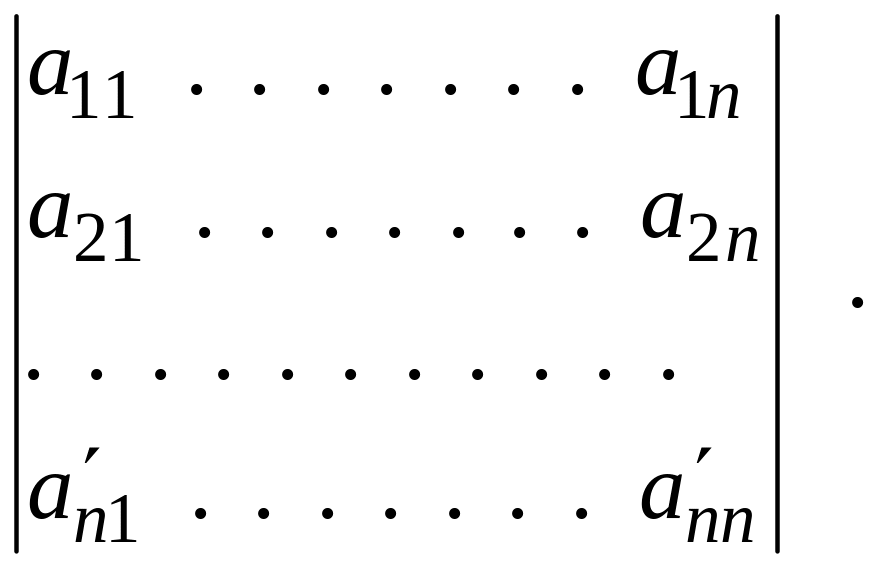
Доказательство.
Определитель
матрицы
записывается формулой
где суммирование
ведётся по всем подстановкам
а
обозначает количество инверсий в
подстановке
Поэтому
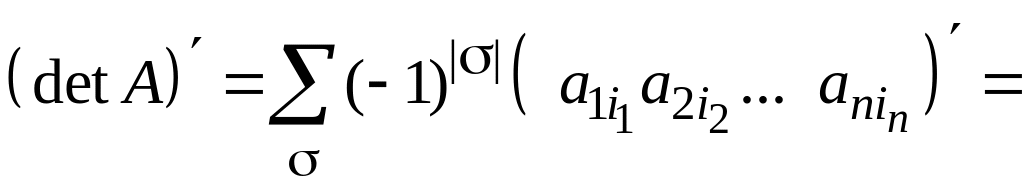
откуда следует требуемое равенство.
Комплекснозначная
функция
действительного аргумента
определяется как функция от
значения которой – комплексные числа.
Она может быть представлена в виде
где
а
обычные действительные функции. Функцию
можно рассматривать как вектор-функцию
поэтому для производной имеет место
равенство
Проверим, что для комплексных функций действительного аргумента справедливо равенство
(9)
Действительно,
пусть
Тогда
поэтому
С другой стороны,
Видно, что эти выражения совпадают.
Для дифференциальных
уравнений с постоянными коэффициентами
имеет важное значение функция
где
.
Воспользуемся для преобразования этого
выражения формулой
Эйлера:
Если
где
,
то
Докажем, что для
комплексного числа
имеет место обычная формула
Действительно,
Разбор типовых примеров
Пример 1.
Доказать формулу
где
и
матрицы размеров
и
соответственно.
Решение.
-й
элемент произвольной матрицы Х
будем обозначать символом
Пусть
Тогда
Отсюда
Пример 2.
Вывести формулу дифференцирования
смешанного произведения
векторов.
Решение.
Пример 3.
Доказать, что если вектор
имеет постоянную длину, то векторы
и
перпендикулярны друг другу.
Решение.
Так как
то скалярное произведение
Отсюда получаем:
Отсюда получаем:
т.е.
Это означает, что
Пример 4.
Пусть
действительная функция, а
комплекснозначная. Доказать, что
Доказательство. Пусть где действительные функции. Тогда
Задачи для самостоятельного решения
1.
Пусть
квадратная
-матрица.
Выразить через
и
производные:
а)
б)
(в случае, когда
в)
где
обозначает транспонирование.
2.
Доказать, что
где
.
3.
Доказать, что для комплекснозначных
функций
действительного аргумента справедлива
формула
