• 3 Рабочий процесс резания

• Для машин с плоским рабочим органом

• Лобовое резание

Расчетная схема лобового резания грунта изображена на рисунке 3.1. Введем некоторые ограничения, принятые при разработке теоретических положений:

- рассматривается процесс резания с элементной или ступенчатой стружкой, т. е. при разрушении грунта за счет сдвига;

- рассматривается установившийся процесс резания, при котором объем призмы грунта ОВКD, находящейся на ноже, и толщина срезаемой стружки будут постоянными;

- влияние затупления режущей кромки не учитывается;

- рассматривается резание при малой скорости, при которой ее влиянием можно пренебречь;

- принимается, что после сдвига грунта по какой-то площадке, на ней действует остаточное удельное сцепление с_о, равное

с_о=k_с_n ,

где _n – нормальное давление на площадку сдвига; k_c – экспериментальный коэффициент пропорциональности.

На необходимость учета остаточного сцепления указывается многими авторами, например. Что касается скорости резания, то рядом авторов отмечено некоторое увеличение сопротивления резанию при увеличении скорости. Однако при низких скоростях (до 1,25 м/с по /116/, до 2 м/с по /26, 50/) ее влияние не существенно и его можно не учитывать. В этом случае, при высоких концентрациях и низких скоростях сдвига частицы грунта находятся в тесном контакте, напряжения не зависят от скорости, и имеет место механизм возникновения напряжений за счет сухого кулоновского трения. При больших скоростях механизм разрушения грунта будет иным, что требует иных методов исследований.

Рисунок 3.1­Схема процесса резания: а)­ расчетная схема при большом сдвиге; б)­ схема сил, действующих на площадку сдвига.

Исходными геометрическими данными, характеризующими нож и условия его работы, будут являться угол резания , длина ножа l_BK, толщина стружки h, ширина ножа B, угол большого сдвига ψ (на данном этапе неизвестный).

Будем считать так же известными с учетом отмеченного выше коэффициента пропорциональности k_c следующие физико-механические свойства грунта:

- угол внутреннего трения ρ;

- угол внешнего трения ω;

- удельное сцепление грунта ненарушенной структуры с и нарушенной структуры с_р;

- плотность грунта в призме, перемещаемой по поверхности ножа ^r;

- коэффициент бокового давления ξ.

Расчет параметров при большом сдвиге

В соответствии с расчетной схемой, изображенной на рисунке 3.1, длина l_OB площадки сдвига ОВ и толщина h́ перемещаемой по ножу призмы грунта OBKD определятся следующим образом

; (3.2)

. (3.3)

Тогда площадь S_OBKD боковой поверхности призмы грунта OBKD будет равна

,

а вес этой призмы G определится по формуле

, (3.4)

где B - ширина ножа.

Рассмотрим разрушение грунта по площадке ОВ, расположенной под некоторым углом ψ к горизонту, во второй фазе, при «течении» грунта. В этом случае на призму ОВКD кроме собственного веса G действуют со стороны ножа и площадки сдвига следующие силы:

R^max - реакция со стороны ножа, отклоненная под углом внешнего трения ω от нормали к ножу;

E^max - реакция со стороны площадки сдвига, отклоненная под углом внутреннего трения  от нормали к площадке;

- сила сцепления грунта по площадке сдвига.

Силу сцепления, действующую в момент сдвига, можно найти так

. (3.5)

Тогда проекции всех сил, воспринимаемых призмой OBKD, на оси X и Y будут выглядеть так

Отсюда

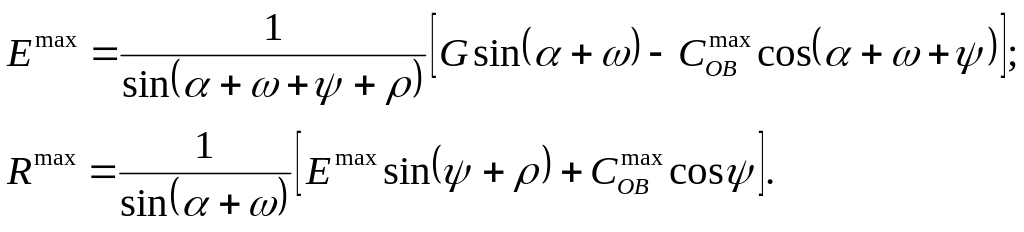
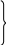(3.6)

Определим приведенное давление, действующее на откос ОВ при сдвиге грунта, исходя из силы E^max.

Приведенная сила Q^max, действующая на откос ОВ, в соответствии со схемой (рисунок 3.1, б) будет равна

. (3.7)

Тогда приведенное давление можно найти, разделив силу Q^max на площадь откоса ОВ

^. (3.8)

При этом угол отклонения этого давления от нормали будет равен _max=ρ. Ввиду того, что приведенное давление, в свою очередь, зависит от угла сдвига ψ, т.е., имеет вид q=f(ψ), то для определения угла большого сдвига необходимо решать совместно систему уравнений. В эту систему входят уравнения (2.14), (2.20), (2.36) типа ψ=f(q), и уравнение (3.8) типа q=f(ψ) вкупе с дополнительными уравнениями, их обслуживающими. Система уравнений решается итерационными методами.

После определения угла сдвига, используя уравнения (3.5) и (3.6), можно рассчитать значения силовых параметров, характеризующих процесс резания, и действующих непосредственно в момент большого сдвига грунта по площадке скольжения ОВ.

После сдвига на этой площадке будет действовать остаточное сцепление, зависящее от величины нормальных давлений на площадку (уравнение (3.1)). Определим величину силы остаточного сцепления, пропорциональную нормальной к рассматриваемой площадке ОВ силе N=E^mincosp:

. (3.9)

Силы E^min и R^min, действующие после сдвига, определим, как и в предыдущем случае, исходя из проекций на оси X и Y сил, воспринимаемых призмой грунта OBKD после сдвига

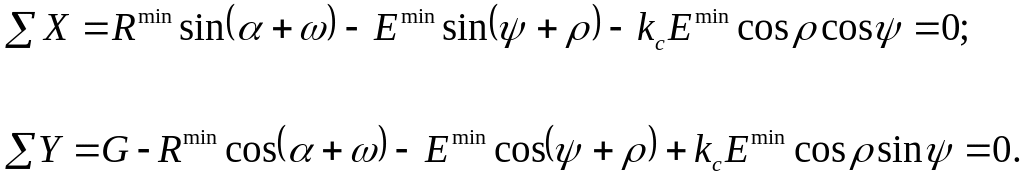
Отсюда получим, что

3.10

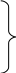
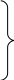Если силами остаточного сцепления пренебречь, то уравнения 3.10 примут вид

3.11

Исходя из схемы на рисунке 3.1, составляющие сопротивления резанию можно найти следующим образом:

3.11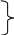

P₁=R sin(a+);

P₂=R cos(a+).

Для определения сил P₁^max и P₂^max, действующих в момент сдвига, в уравнения (3.11) вместо R следует подставлять значение силы R^max, полученное из уравнений (3.6). Для определения сил P₁^min и P₂^min, действующих после сдвига  значение силы R^min из уравнений (3.10).

Амплитуда колебаний составляющих сопротивления резанию при достаточно быстро протекающем процессе сдвига грунта определится так

3.12

Полученные уравнения обеспечивают расчет геометрических и силовых параметров, характеризующих лобовое резание грунта.