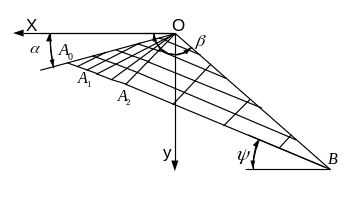
Решения с сингулярной точкой при вершине откоса

Сингулярной считается точка, в которой пересекается пучок линий скольжения. Физически это означает локализацию условия разрушения или нарушение непрерывности напряжений.

Рисунок 2.7­ Расчетная схема с сингулярной точкой.

Расчетная схема такого случая представлена на рисунке 2.7. Уравнения, характеризующие напряженное состояние в пассивной А₀OA₁ и активной А₂ОВ зонах в общем случае имеют вид, вытекающий из условий (1.5):

- для пассивной зоны А₀ОА₁, при χ=+1

(2.5)

- для активной зоны A₂OB, при χ =-1

(2.6)

где ₁ и ₂ - средние приведенные нормальные напряжения в зонах A₀OA₁ и A₂OB; p и q - приведенные давления, действующие на поверхность засыпки и откос OB; ₁ и  - углы отклонения приведенных давлений p и q; ₁ - угол наибольших главных напряжений в зоне А₀ОА₁ относительно оси Х; и ₂ - углы наибольших главных напряжений в зоне А₂ОВ соответственно относительно откоса ОВ и оси Х (углы ₁, и ₂ изображены на рисунке 2.5);  - угол при вершине откоса.

Углы ₁ и  в соответствии с уравнением (1.7) будут равны

.

Применительно к рассматриваемой задаче, когда призма волочения отсутствует, а поверхность грунта находится под действием всестороннего нормального давления связности Н, углы δ₁ и Δ₁ равны нулю, и при этом

,

уравнения (2.5) предельного состояния грунта в зоне A₀OA₁ примут вид

. (2.6а)

При условии  и =  уравнения (2.6) предельного состояния грунта в зоне А₂ОВ будут выглядеть следующим образом

(2.7)

Для рассматриваемой схемы значение σ=σ₂ в точке О, принадлежащей зоне А₂ОВ, должно быть больше, чем значение σ=σ₁ в точке О, принадлежащей зоне А₀ОА₁, т.е. σ₂σ₁. Подставляя необходимые значения из уравнений (2.5) и (2.7), получим условие существования рассматриваемого расчетного случая с сингулярной точкой

(2.8)

Для характеристики в точке О зоны А ОА имеем

Для точки О, принадлежащей зоне А ОА , с учетом уравнений (1.11), (1.14) и (2.5), будем иметь

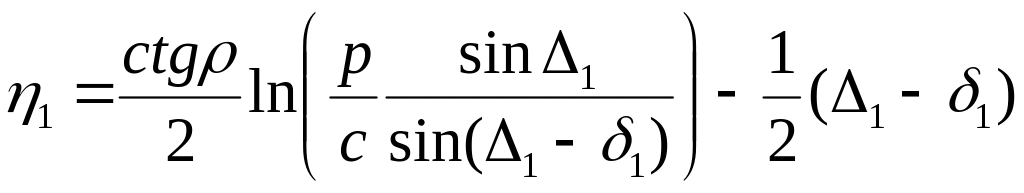, (2.9)

а для точки О, расположенной в зоне с учетом  и для этой зоны по уравнениям (2.6) аналогичным образом получим:

(2.10)

При p=H, δ₁=0 и Δ₁=0 уравнение (2.9) будет выглядеть так

. (2.10, а)

Уравнение (2.10) при примет вид

. (2.11)

А так как , то

. (2.12)

Обозначив

, (2.13)

перейдем к углу сдвига ψ. Так как при  имеем ψ , то в полном виде получим

. (2.14)

Отметим, что схемы на рисунках 2.6, 2.7 и 2.10 изображены при углах  ввиду невозможности изображения их при углах . При  зона стягивается к откосу ОВ, а пассивная зона - в точку О, что хорошо видно из рисунка 2.4.

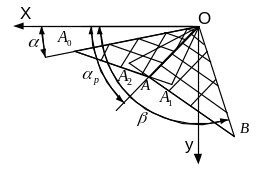
Разрывные решения.

Если условие (2.8) не будет выполнено, то в зоне разрушения образуется линия разрыва, вблизи которой хотя и сохраняется равновесие, но нет полной непрерывности напряжений. Расчетная схема для такого случая изображена на рисунке 2.8.

Для зоны А₀ОА по-прежнему остаются в силе уравнения (2.5). Относительно углов _р и _р на линии разрыва ОА для этой же зоны имеем из уравнений (1.5) при χ=+1

₊= (  ) и

= + = + ( - ), (2.15)

где - угол наклона линии разрыва; - угол отклонения приведенного давления на линии разрыва, а угол Δ_р будет равен

= arcsin .

Рисунок 2.8­ Расчетная схема с линией разрыва.

Но для одной и той же зоны должно быть = , откуда, с учетом их значений, получим

= (  ). (2.16)

Аналогично для зоны АОВ имеем, с одной стороны, уравнения (2.7), а с другой стороны из (1.5) при χ= 1 получим

=

(2.17)

Заменяя в полученном уравнении (2.17) значение его выражением (2.16), получим

. (2.18)

Так как в зоне АОВ , то из (2.7) и (2.18) получим

(2.19)

Переходя к углу сдвига , имеем

. (2.20)

Из уравнения (2.20) видно, что для определения угла сдвига , кроме граничных условий на засыпке массива, необходимо знать величину угла . Определим ее. Условия разрыва могут быть получены из уравнений (1.5), а именно

. (2.21)

Из условий разрыва, с учетом того, что а , имеем

. (2.22)

Перепишем уравнение (2.22) с учетом уравнения (2.13) таким образом

,

или

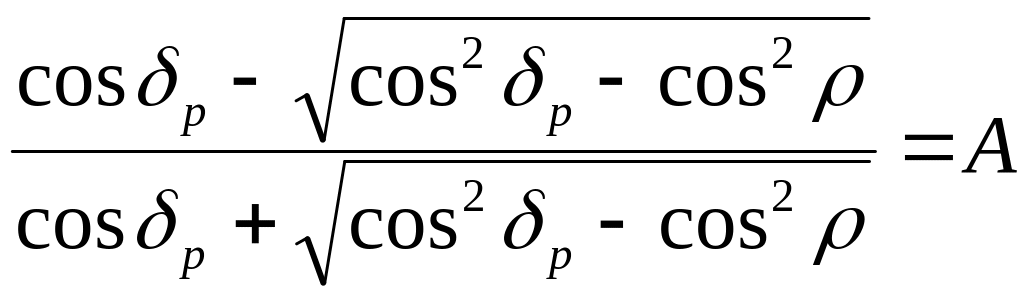, (2.23)

а его решение после ряда преобразований получим в виде

и, как и раньше,

. (2.24)

Уточним условия существования разрывных решений.

Рассмотрим случай, когда линия разрыва OA будет совпадать с поверхностью засыпки, т. е. _p=0. Из уравнения (2.21) с учетом уравнений (2.5) и (2.6) при ₊=₁ и _-=₂ получим в общем виде

. (2.25)

Так как _p=0 и, следовательно, _p=0, _p=0 и при условии, что , , справедливом для рассматриваемой задачи, предельное давление будет равно

. (2.26)

Следовательно, относительно границ области разрывных решений выполняется следующее неравенство, полученное с учетом неравенства (2.8)

. (2.27)

Действительно, при имеем из уравнения (2.16), что

.

Это значит, что с линией разрыва совпадают линия скольжения ОА₁ второго семейства линий скольжения зоны А₀ОА₁ и линия скольжения ОА₂ второго семейства линий скольжения зоны А₂ОВ, и справедливо условие (2.8). Этот случай находится на границе двух типов решений - с сингулярной точкой и с линией разрыва и разделяет их.

Таким образом, условие (2.27) полностью охватывает область существования разрывных решений, в которой значение δ_р изменяется в пределах -ρ δ_р 0, что необходимо иметь ввиду при использовании уравнений (2.24).