Расчет мольной доли отгона сырья, поступающего в колонну
Расчет мольной доли отгона сырья при температуре и давлении в секции питания проводится итерационным методом с использованием уравнений Трегубова [1] :
(17)
(18)
Мольная доля отгона может быть, в принципе, рассчитана по любому из вышеприведенных уравнений. Однако, для лучшей сходимости целесообразно использовать целевую функцию, предложенную Ричмондом и Райсом, которая получается объединением уравнений (17) и (18):
(19)
Соответствующий алгоритм Ньютона-Рафсона будет выглядеть следующим образом:
(20)
В
качестве начального приближения можно
выбрать любое значение
,
лежащее в пределах от 0 до 1 (рекомендуется
=
0.5).
Следует
отметить, что температура и давление
однократного испарения сырья должны
обеспечивать его двухфазное состояние.
Для этого необходимо одновременное
выполнение двух условий:
и
.
В нашем случае
,
а
,
т.е. требуемые условия выполняются.
Результаты расчета мольной доли отгона сырья и составов жидкой и паровой фаз при полученном значении = 0.11 приведены в таблице 5.
Таблица 5 - Результаты расчета мольной доли отгона сырья
Компонент |
,мол.д |
Pi0, МПа |
Кi |
= 0.11 |
|
|
|
||||
изобутан |
4.99 |
8.944 |
3.578 |
3.9 |
1.395 |
н-бутан |
4.99 |
6.63 |
2.652 |
4.233 |
0.011 |
изопентан |
0.422 |
2.853 |
1.141 |
0.416 |
0.475 |
н-пентан |
0.563 |
2.239 |
0.896 |
0.569 |
0.51 |
н-гексан |
7.74 |
8.026 |
0.321 |
8.361 |
2.684 |
н-гептан |
1.59 |
2.967 |
0.119 |
1.761 |
2.09 |
Всего |
1.0000 |
|
|
1.000 |
1.000 |
1.6 Расчет минимального флегмового числа
Минимальное флегмовое число рассчитывается с использованием уравнений Андервуда [1] :
;
(21)
(22)
Средние геометрические значения коэффициентов относительной летучести i по отношению к наиболее высококипящему компоненту (ВКК) сырья рассчитываются по формуле:
(23)
Вспомогательный коэффициент подбирается методом последовательных приближений, при этом должно выполняться условие:
ТКК ЛКК (24)
Поэтому
в качестве начального приближения
следует выбрать значение ,
лежащее в пределах от ТКК
до ЛКК
(рекомендуется
(0)
=
).
В противном случае полученный корень
уравнения не будет иметь физического
смысла. Алгоритм Ньютона-Рафсона будет
выглядеть следующим образом:
(25)
Результаты
расчета значения
при начальном приближении
приведены в таблице 6.
Таблица 6 - Результаты расчета коэффициента
Компонент |
i, в |
i, н |
i |
ХFi |
|
|
|
|
|
|
|
изобутан |
34.786 |
25.84 |
29.981 |
4 |
|
н-бутан |
25.506 |
19.369 |
22.227 |
4 |
|
изопентан |
10.68 |
8.578 |
9.571 |
0.42 |
|
н-пентан |
8.262 |
6.841 |
7.518 |
0.561 |
|
н-гексан |
2.833 |
2.574 |
2.7 |
9.2 |
|
н-гептан |
1 |
1 |
1 |
2.2 |
|
Всего |
|
|
|
1.0000 |
8.581 |
Принимаем = 8.581
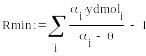
С учетом коэффициента избытка флегмы рабочее флегмовое число:
R = 1.2.Rmin (26)
R = 1.2.2.874 = 3.448