2.1 Определение неопределенного интеграла

Дадим строгое математическое определение понятия неопределенного интеграла.

Выражение вида   называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.

Определение. Неопределенным интегралом  называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.  или  Функцию   называют первообразной функции   . Первообразная функции   определяется с точностью до постоянной величины.

Напомним, что   -дифференциал функции   и определяется следующим образом:

Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.

Например, известно, что   , тогда получается, что   , здесь   - произвольная постоянная.

Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы снеопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях. 

2.2 Свойство линейности для неопределенного интеграла

Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.

1. Из определения вытекает, что

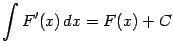
и

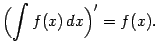
Второе равенство нужно понимать так, что производная любой из функций, составляющих неопределённый интеграл, даёт один и тот же результат, равный подынтегральной функции (это как раз и есть определение первообразной). Два написанных равенства выражают взаимную обратность операций дифференцирования и интегрирования.

2. Имеет место равенство:

где    -- произвольная постоянная. Для доказательства обозначим через   некоторую первообразную для   , а через    -- некоторую первообразную для   . Тогда равенство означает, что   , где    -- постоянная. Это равенство верно, поскольку производные левой и правой частей дают одно и то же:   , так как    -- первообразная для   , а   , так как постоянный множитель можно вынести за знак производной и   .

Итак, постоянный множитель можно вынесить за знак интеграла.

3. Интеграл от суммы равен сумме интегралов:

Действительно, пусть первообразная для   равна   , для   равна   , а для   равна   . Тогда равенство означает, что

где   . Поскольку

и

то равенство верно; при этом мы воспользовались тем, что производная суммы равна сумме производных.

Свойства 2 и 3 называются свойствами линейности неопределённого интеграла. Из них следует, что для любых постоянных   и 

и, в частности,

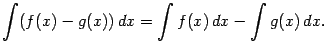
2.3 Метод интегрирования заменой переменой

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

2.4 Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарнойфункцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

Предполагается, что нахождение интеграла   проще, чем  . В противном случае применение метода неоправдано.