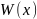- •Метод Ейлера для розв’язування задач Коші
- •Вдосконалений метод Ейлера
- •Метод Ейлера-Коші
- •Збіжність методу Ейлера
- •Методи Рунге-Кутта
- •Метод Рунга-Кута 3-го порядку
- •Метод Рунга-Кута 4-го порядку
- •Методи розв’язання лінійних рівнянь та їх систем
- •Метод Ньютона для відшукання верхньої межі коренів
- •Метод Штурма
- •Метод простої ітерації
- •Метод хорд
- •Метод Ньютона
- •Комбіновий метод хорд і дотичних
- •Метод січних
- •Метод поділу відрізка пополам
- •Збіжність методу простої ітерації
- •Збіжність методу Ньютона
- •Ітераційні методи для систем нелінійних рівнянь
- •Метод релаксації
- •Метод Пікара
- •Метод Ньютона
- •Модифікований метод Ньютона
Метод Ньютона для відшукання верхньої межі коренів
Розглянемо рівняння виду , де рівняня з дійсними коефіцієнтами , то ді буде справедлива теорема
Теорема
Якщо
для
 виконується
виконується тоді
число
тоді
число
 є верхньою межею коренів
рівняння.
є верхньою межею коренів
рівняння.
Знаходити число можна наступним чином
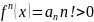 тоді
тоді
 є зростаючою функцією аргумента
Тоді знайдеться деяке число
є зростаючою функцією аргумента
Тоді знайдеться деяке число
 ,
що при
,
що при
 .
Тоді
.
Тоді
 є зростаючою функцією аргумента
,
Тоді знайдеться деяке число
є зростаючою функцією аргумента
,
Тоді знайдеться деяке число
 ,
що при
,
що при
 і так далі ……
і так далі ……
 є зростаючою функцією
є зростаючою функцією
 .
.
 може бути верхньою межею
коренів рівняння
може бути верхньою межею
коренів рівняння

Приклад






Метод Штурма
Розглянемо
рівняння виду
,
з
 коефіцієнтами, яке не має
кратних коренів. Складемо систему
функцій Штурма
коефіцієнтами, яке не має
кратних коренів. Складемо систему
функцій Штурма
 де
де
 остача від ділення
остача від ділення
 взята з протилежним знаком
взята з протилежним знаком
 остача від ділення
остача від ділення
 взята з протилежним знаком
взята з протилежним знаком

Система функцій виду (5), а також будь-яка інша отримана з (5) шляхом множення на деякий додатній коефіцієнт називається системою функцій Штурма
 система
функцій Штурма збігається з (5) з точністю
до сталого додатного множника.
система
функцій Штурма збігається з (5) з точністю
до сталого додатного множника.
Нехай
всі корені виду (2) містяться на проміжку
 .
.


 кількість
перемін знаком у системі функцій (7)
кількість
перемін знаком у системі функцій (7)
 кількість
перемін знаком у системі функцій (8)
кількість
перемін знаком у системі функцій (8)
Теорема
Якщо рівняння
виду
 немає кратних коренів і
немає кратних коренів і
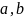 не
є коренями цього рівняння, то
не
є коренями цього рівняння, то
 і
і
 кількості
кількості
 коренів які розташовані на проміжку
.
коренів які розташовані на проміжку
.
Приклад.
Відокремити корені рівняння
 .
.
Знаходимо
межі коренів рівняння:
 верхня
межа,
верхня
межа,
 по
Маклорена
по
Маклорена
Нижня межа










|
|
|
|
|
|
-4 |
|
|
|
|
3 |
2 |
|
|
|
|
0 |

|
|
|
|
|
|
-4 |
|
|
|
|
3 |
2 |
|
|
|
|
0 |
-3 |
|
|
|
|
3 |
-2,1 |
|
|
|
|
2 |
-1 |
|
|
|
|
2 |
0,1 |
|
|
|
|
1 |
1 |
|
|
|
|
0 |






Методи уточнення коренів. Ітераційні методи розв’язання алгебраїчних та рівнянь
Нехай нам
потрібно розв’язати алгебраїчне
рівняння
 .
.
Нехай
відомо достатньо малий проміжок на
якому міститься один корінь
 виберемо
деяке початкове наближення на цьому
проміжку
виберемо
деяке початкове наближення на цьому
проміжку
 і за допомогою деякого рекурентного
співвідношення
і за допомогою деякого рекурентного
співвідношення
 будуємо
послідовність точок
будуємо
послідовність точок
 що
буде збігатися до розвязку
що
буде збігатися до розвязку


Збіжність
послідовності
 забезпечуємо вибором функції
забезпечуємо вибором функції
 .
Зазвичай у нас використовується
залежність
.
Зазвичай у нас використовується
залежність
 він є одночасно розв’язком
рівняння (1)і(3). Будемо підбирати і
будувати інтерполяційний процес за
формулою
він є одночасно розв’язком
рівняння (1)і(3). Будемо підбирати і
будувати інтерполяційний процес за
формулою
Метод простої ітерації
Нехай маємо
,
 на якому міститься один
корінь
і
маємо початкове наближення
дане рівняня перепишемо у
вигляді
на якому міститься один
корінь
і
маємо початкове наближення
дане рівняня перепишемо у
вигляді
 .
.
Від (1) до (2) ми можемо перейти різними способами де функцію можемо вибирати як
 ,
,
 деяка функція яка зберігає
свій знак на проміжку
,
дана функція може бути вибрана
як константа.
деяка функція яка зберігає
свій знак на проміжку
,
дана функція може бути вибрана
як константа.
Покажемо що при такому виборі рівняння (1)і(2) були еквівалентними
Нехай
є коренями рівняння


Припустимо
що
 є розв’язком рівняння (2)
є розв’язком рівняння (2)
 ;
;
 маючи початкове наближення, згідно
методу простої ітерації, кожне наступне
наближення буде вибиратися
маючи початкове наближення, згідно
методу простої ітерації, кожне наступне
наближення буде вибиратися
Згідно методу
простої ітерації


Умова завершення ітераційного процесу

Збіжність методу простої ітерації буде визначатися нерівністю





Збіжність методу буде з того боку з якого виберемо початкове наближення
Розглянемо односторонню збіжність