
- •2) A) Естественный способ задания движения.
- •3) А) Скорость точки при векторном способе задания движения
- •5 ) Дифференцирование единичного вектора
- •7) А) Ускорение точки
- •8) Поступательное движение твердого тела.
- •9) Вращение твёрдого тела вокруг неподвижной оси
- •10) Скорости и ускорения точек тела при вращении.
- •11) Плоское движение твердого тела
- •12) Теорема о проекциях скоростей двух точек тела.
- •13) Мгновенный центр скоростей
- •15) Сложение ускорений в общем случае плоского движения
- •19) Угловая скорость и угловое ускорение при сферическом движении твердого тела
- •20) Разложение движения свободного тела на поступательное и вращательное.
- •21) Относительное, переносное и абсолютное движение точки.
- •22) Teopeмa сложения скоростей.
- •23) Сложение ускорений в общем случае переносного движения
1) Кинематикой называется раздел теоретической механики, в котором изучается механическое движение без учета действующих сил.
2) A) Естественный способ задания движения.
Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. В зависимости от вида траектории движение называют прямолинейным или криволинейным. S = f(t)
Чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки. 2) начало отсчета на траектории с указанием
направления
движения (![]() ),
3) закон движения точки вдоль траектории
в виде. Здесь необходимо заметить, что
S определяет положение точки на траектории,
а не пройденный путь.
),
3) закон движения точки вдоль траектории
в виде. Здесь необходимо заметить, что
S определяет положение точки на траектории,
а не пройденный путь.
б) Координатный способ задания движения.
Положение точки по отношению к данной системе отсчета O,x,y,z можно определить с помощью координат x,y,z . При движении точки М вдоль траектории, с течением времени, координаты будут изменяться и чтобы задать закон движения точки, нужно задать зависимости:
![]()

Соотношения (8.2.2) представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они представляют собой и параметрические уравнения траектории. Исключив параметр t, получим уравнение траектории через координаты.
в) Векторный способ.
Положение точки можно определить с помощью радиуса-вектора г, проведенного из некоторой заданной неподвижной точки О в данную точку М При движении точки радиус-вектор г изменяется по величине и направлению Каждому моменту времени г соответствует свое значение г. Следовательно, г является функцией времени г: г = r (t)
3) А) Скорость точки при векторном способе задания движения
П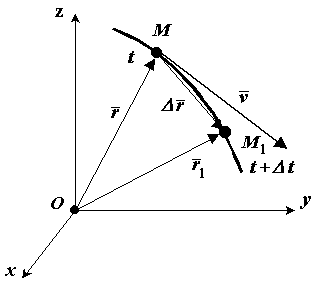 оложение
движущейся точки М относительно системы
отсчета в момент времени
оложение
движущейся точки М относительно системы
отсчета в момент времени
 определяется радиус-вектором
определяется радиус-вектором
 .
В другой момент времени
.
В другой момент времени
 точка займет положение М1 с радиус-вектором
точка займет положение М1 с радиус-вектором
 .
За время
.
За время
 радиус-вектор движущейся точки изменится
на
радиус-вектор движущейся точки изменится
на
 .
.
Средней
скоростью
 называется отношение изменения
радиус-вектора
называется отношение изменения
радиус-вектора
 к изменению времени
.
к изменению времени
.

Скорость точки равна первой производной по времени от ее радиус-вектора.

б) Скорость точки при координатном способе задания движения
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим

После дифференцирования
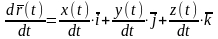
Отсуда следует


 (1-8)
(1-8)
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
Модуль скорости и направляющие косинусы равны:

в) Скорость точки при естественном способе задания движения.
Пусть
скорость точки задана естественным
способом, т.е. заданы траектория точки
и закон ее движения по траектории
 .
.
Вычислим скорость точки.
И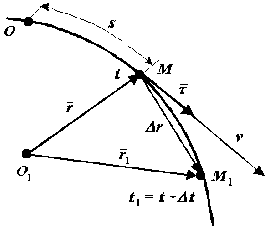 спользуем
радиус-вектор
.
движущейся точки, начало которого
находится в неподвижной точке
спользуем
радиус-вектор
.
движущейся точки, начало которого
находится в неподвижной точке

 - единичный вектор,
направленный по касательной к траектории
в сторону возрастающих расстояний.
- единичный вектор,
направленный по касательной к траектории
в сторону возрастающих расстояний.
 - алгебраическая
скорость точки, проекция скорости
- алгебраическая
скорость точки, проекция скорости
 на положительное направление касательной
к траектории.
на положительное направление касательной
к траектории.
4) Годографом вектора скорости является кривая линия, на которой располагаются концы этого вектора в различные моменты времени, если их начала совместить в одной общей точке.
