
- •Особливості курсу
- •Етапи розв’язку прикладної задачі на еом
- •1. Класифікація рівнянь в частинних похідних.
- •2. Основні типи рівнянь математичної фізики.
- •3. Постановки крайових задач для основних рівнянь математичної фізики еліптичного та параболічного типів.
- •3.1 Канонічні рівняння еліптичного типу – рівняння Лапласа та Пуассона.
- •3.2. Канонічні рівняння параболічного типу – рівняння теплопровідності, конвективної дифузії
- •3.2.1. Рівняння теплопровідності
- •3.2.2. Рівняння конвективної дифузії мігруючих речовин в деякому пористому середовищі (наприклад, водорозчинних речовин в ґрунті) має вид:
- •3.3. Крайові умови та їх види
- •3.3.1 Задання початкової умови (для рівнянь параболічного типу – теплопровідності та дифузії)
- •3.3.2 Задання граничних умов.
- •3.4.Постановка крайових задач для рівнянь еліптичного типу
- •3.5. Постановка крайових задач для рівнянь параболічного типу
- •4. Методи розв’язування задач для рівнянь в частинних похідних
- •5. Суть методу скінчених різниць (сіток). Елементарні відомості з теорії різницевих схем
- •5.1. Ідея методу скінчених різниць (сіток)
- •5.2. Елементарні поняття з теорії різницевих схем
- •6. Чисельне розв’язування крайових задач для рівнянь еліптичного типу.
- •6.1. Апроксимація похідних (сіткова апроксимація)
- •6.2. Різницева апроксимація задачі Діріхле для рівнянь Лапласа та Пуассона
- •6.3. Чисельний метод розв’язування різницевої схеми (6.7), (6.8).
- •6.4 Алгоритм ручного рахунку задачі Діріхле.
- •Лабораторна робота №1.
- •Порядок виконання роботи.
- •Контрольні запитання.
- •Деякі узагальнення методу скінченних різниць та його недоліки.
- •7. Різницеві схеми для рівнянь теплопровідності.
- •7.1 Явна різницева схема
- •7.1.1 Алгоритм ручного рахунку
- •7.2 Неявна різницева схема.
- •7.3 Лабораторна робота №2
- •Порядок виконання роботи.
- •Контрольні запитання.
- •8. Різні сімейства різницевих схем для рівняння теплопровідності
- •8.1 Деякі позначення
- •8.2 Різні сімейства різницевих схем для рівняння теплопровідності
- •8.3 Різницеві схеми для рівняння теплопровідності із змінними коефіцієнтами
- •8.4.Різницеві схеми для нелінійного рівняння теплопровідності.
- •9. Монотонні різницеві схеми для рівнянь параболічного типу, що містять перші похідні
- •9.2 Монотонні рс для звичайного рівняння другого порядку, що містить перші похідні
- •9.3 Монотонна різницева схема для параболічного рівняння
- •10. Інтегро-інтерполяційний метод побудови рс.
- •10.1 Вступ. Методи побудови рс
- •10.2 Приклади побудови рс інтегро-інтерполяційним методом.
- •11. Різницеві схеми для рівнянь гіперболічного типу.
- •Різницева схема для рівняння коливання
- •1. Постановка задачі.
- •2. Різницева апроксимація задачі (1)-(3)
- •13. Економічні методи розв’язання крайових задач математичної фізики.
- •13.1 Економічні методи розв’язання першої крайової задачі для двовимірного рівняння теплопровідності.
- •Стійкість поперечно-поздовжньої рс
- •14. Загальні відомості з теорії стійкості рс.
- •1. Канонічний вигляд двохшарових рс.
- •2. Теорема про стійкість по початкових даних
- •Сумарна апроксимація
- •Локальна одновимірна схема Салмарського
- •1. Вступ
- •2. Основна концепція мсе
- •Переваги і недоліки мсе
- •Математичні основи методу мсе
- •Кусково-визначені базисні функції і мсе.
- •Поняття скінченого елемента.
- •V. Питання гарантованого рівня знань
Сумарна апроксимація
Принцип
сумарної апроксимації полягає в
наступному: кожне з рівнянь (0)-(1) апроксимує
вихідне диференціальне рівняння (1) з
першого пункту (РС звагами для двохвимірного
рівняння ) з точністю 0(+h²).
При переході з цілого шару k
на шар k+½
кожна просторова різниця обчислюється
несеметрично по часу і похибка апроксимації
кожної з РС рівна 0(τ+h²).
Але похибка на другій половині шару по
часу компенсує першу і в сумі при переході
з цілого шару k
на k+1
,
тоді похибка має такий порядок апроксимації
![]() ).
Математично це має такий вигляд :
).
Математично це має такий вигляд :
***Схема
стійка при будь-яких кроках
![]() і h.
Схему змінніх напрямків можна досліджувати
двояко
і h.
Схему змінніх напрямків можна досліджувати
двояко
виключивши
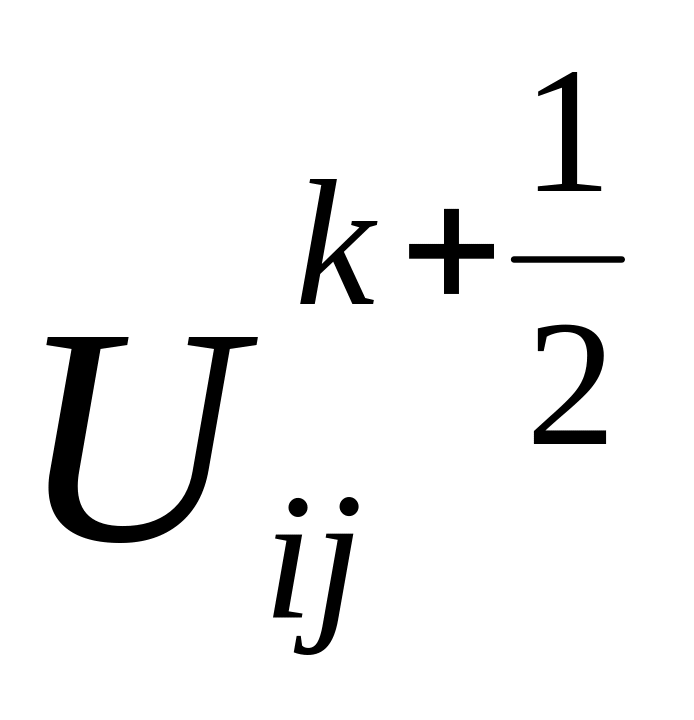 з різницевих рівнянь;
з різницевих рівнянь;безпосередньо шляхом сумарної апроксимації
Нехай
U(x![]() t)-точний
розв’язок
. Представимо розв’язок різницевої
задачі у вигляді:
t)-точний
розв’язок
. Представимо розв’язок різницевої
задачі у вигляді:
![]() (26)
(26)
де
![]() -це
нев’язка, тобто різниця між точним і
наближеним розв’язком.
-це
нев’язка, тобто різниця між точним і
наближеним розв’язком.
![]() (27)
(27)
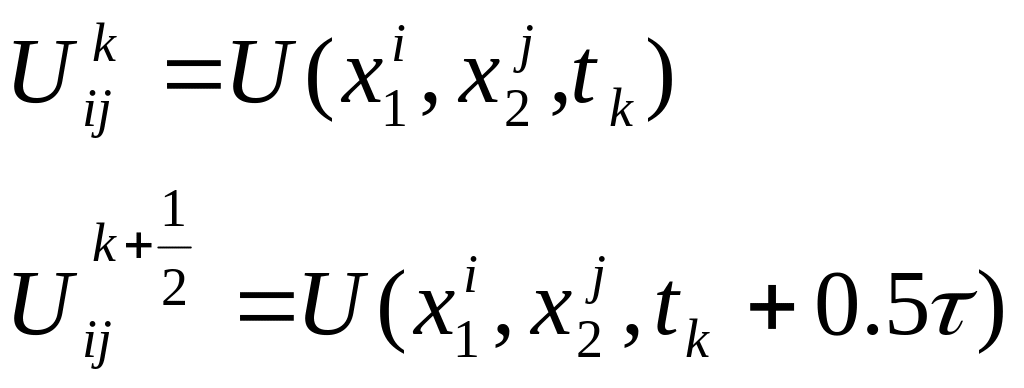
Підставляючи вказані вирази (26), (27) в (10), (11) отримаєм рівняння, які задовольняють похибки методу:

Ці сіткові функції називаються похибками апроксимації різницевої задачі (10)-(11) на розв’язок вихідної задачі (1)-(3).
Розкладаючи
функції, які входять в дані вирази по
формулі Тейлора в околі точки
![]() отримаємо:
отримаємо:
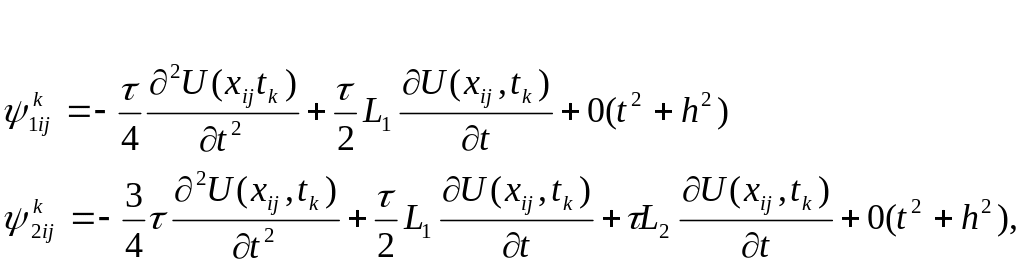
Із (28)
видно, що кожне з різницевих рівнянь
(10)-(11) апроксимує вихідне рівняння з
першим порядком по
і другим порядком по h,
де
![]() ,
,
![]() сумарна
апроксимація (28)
сумарна
апроксимація (28)
Разом з тим, сума похибок апроксимації має другий порядок має другий порядок по і другий порядком по h. Знаходимо сумарну похибку:
![]() (30)
(30)
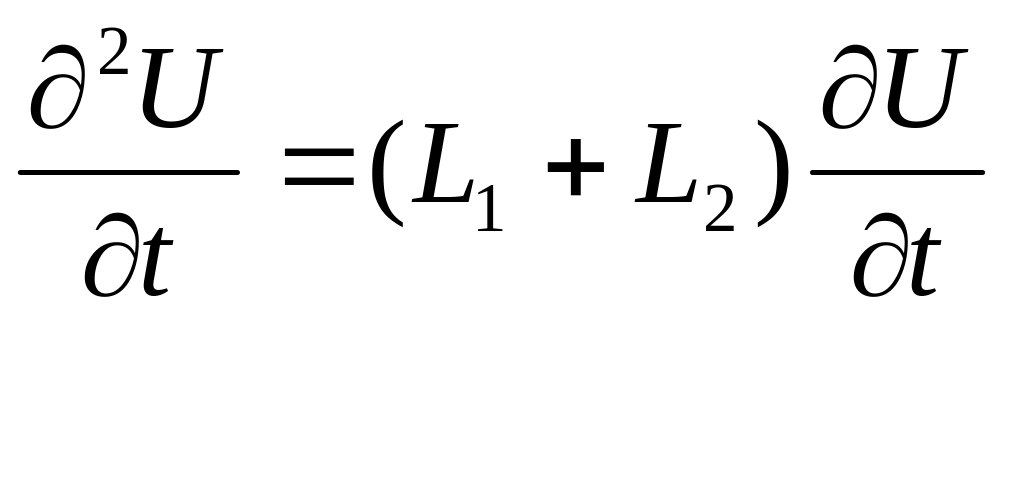 (31)
(31)
![]() (32)
(32)
Кажуть, що схема (10)-(11) володіє сумарною апроксимацією другого порядкупо і другого порядку по h.
Локальна одновимірна схема Салмарського
Наведемо інші РС змінних напрямків для диференціальної задачі (1)-(3), що володіють сумарною апроксимацією.
ЛОС Салмарського складається має вигляд:
 (33)
(33)
 (34)
(34)
Таким чином спростили РС- це схема є ЛОС. Вона володіє розщепленням по координата. В даній схемі кожне з рівнянь (33)-(34) окремо не апроксимує вихідне рівняння (1), однак , в цілому, схема володіє сумарною апроксимацією саме з порядком 0(τ+h²).
Дійсно, покажемо, що має місце така сумарна апроксимація.
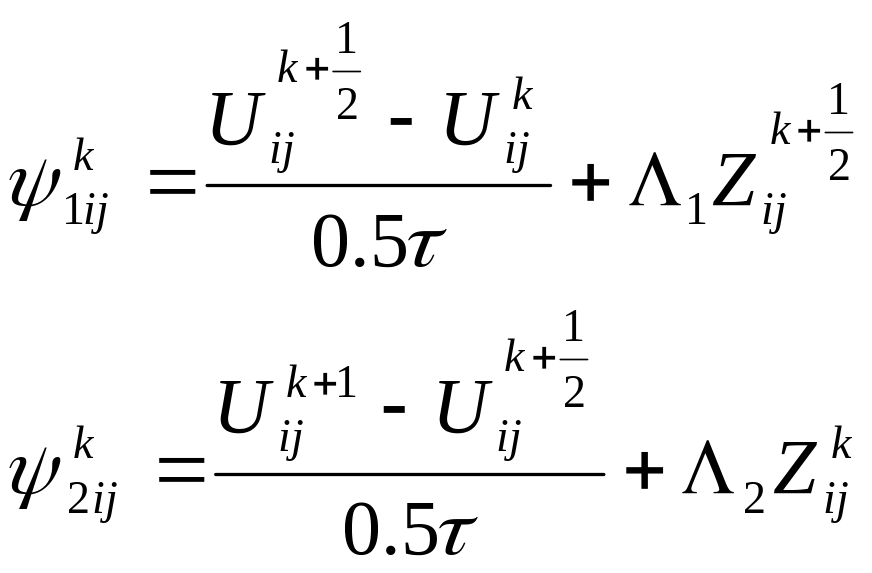

ЛОС
Самарського має порядок апроксимації
![]()
Знаходження
граничних умов для
проводиться аналогічно як і в методі
Письмена-Речфорда. Тобто виразити
з ЛОС через
![]() та довизначити дану РС
та довизначити дану РС
![]() із знайденого виразу
із знайденого виразу
Іноді ЛОС називається схемою розчеплення по координатах . Зауважемо, що в подібних схемах відсутня апроксимація на кожному проміжному етапі, хоча в цілому, схема має сумарну апроксимацію. Тобто, на проміжних етапах використовують одновимірні різницеві схеми, які окремо не апроксимують вихідне рівняння. Тут має місце лише сумарна апроксимація з цілими номерами k.
Похибка апроксимації проміжних номерів при сумуванні знищується. Такі схеми з сумарною апроксимацією називаються адитивними. Схема розщеплення по координатах являє собою неявну двократну схему для одновимірного рівняння теплопровідності. На першому етапі знаходяться допоміжні значення , а на другому шукане значення сіткової функції.
Математичні
висновки для ЛОС аналогічні, як і для
поздовжньо-поперечної різницевої схеми
лише в сторону спрощення , а саме у
рівнянні (2) замість
![]() потрібно взяти
потрібно взяти
![]() , аналогічно і прогоночні коефіцієнти
. У (5) замість
, аналогічно і прогоночні коефіцієнти
. У (5) замість
![]() підставимо
.
підставимо
.
При сумарній апроксимації точність 0(h²+τ).
Системи лінійних рівнянь, що отримуються мають трьох діагональний вигляд. Розв’язуються за допомогою методу прогонки.
Схема
безумовно стійка і вона збігається з
швидкістю
![]()
Із побудови ЛОС видно, що вона легко узагальнюється на випадок довільного числа змінних, при цьому кржна нова змінна вимагає введення одного проміжного етапу на кожному шарі по часу.
Побудуємо ЛОС для задачі (1)-(3). Запишемо ЛОС Самарського (33)-(34) в координатному вигляді:
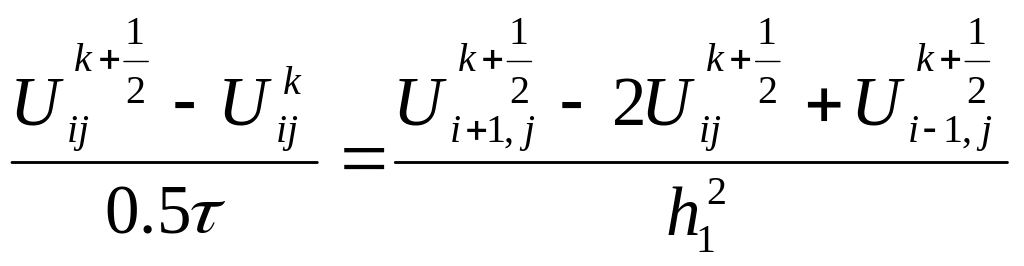 (38)
(38)
 (39)
(39)
(38) в про гоночному вигляді:
![]() (40)
(40)
![]()
![]()
![]()
Про гоночні коефіцієнти:
![]()
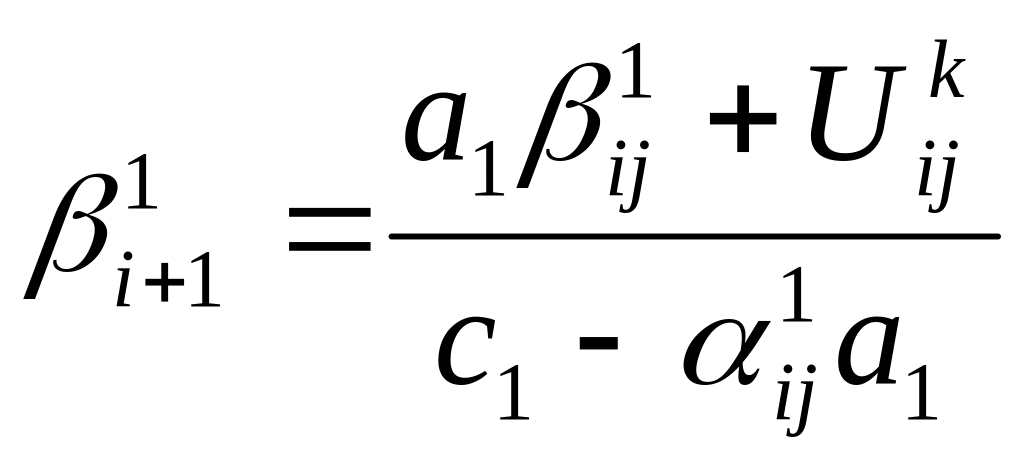 (43)
(43)
![]() (44)
(44)
Інша група методів розщеплення базується на результаті вихідної задачі по фізичних процесах. На кожному шарі по часу вихідна складна задача, що описує деякий фізичний процес при наявності декількох впливових на нього факторів. Розщіплюється на більш прості задачі.
Основи методу скінченних елементів (МСЕ).
