
- •Особливості курсу
- •Етапи розв’язку прикладної задачі на еом
- •1. Класифікація рівнянь в частинних похідних.
- •2. Основні типи рівнянь математичної фізики.
- •3. Постановки крайових задач для основних рівнянь математичної фізики еліптичного та параболічного типів.
- •3.1 Канонічні рівняння еліптичного типу – рівняння Лапласа та Пуассона.
- •3.2. Канонічні рівняння параболічного типу – рівняння теплопровідності, конвективної дифузії
- •3.2.1. Рівняння теплопровідності
- •3.2.2. Рівняння конвективної дифузії мігруючих речовин в деякому пористому середовищі (наприклад, водорозчинних речовин в ґрунті) має вид:
- •3.3. Крайові умови та їх види
- •3.3.1 Задання початкової умови (для рівнянь параболічного типу – теплопровідності та дифузії)
- •3.3.2 Задання граничних умов.
- •3.4.Постановка крайових задач для рівнянь еліптичного типу
- •3.5. Постановка крайових задач для рівнянь параболічного типу
- •4. Методи розв’язування задач для рівнянь в частинних похідних
- •5. Суть методу скінчених різниць (сіток). Елементарні відомості з теорії різницевих схем
- •5.1. Ідея методу скінчених різниць (сіток)
- •5.2. Елементарні поняття з теорії різницевих схем
- •6. Чисельне розв’язування крайових задач для рівнянь еліптичного типу.
- •6.1. Апроксимація похідних (сіткова апроксимація)
- •6.2. Різницева апроксимація задачі Діріхле для рівнянь Лапласа та Пуассона
- •6.3. Чисельний метод розв’язування різницевої схеми (6.7), (6.8).
- •6.4 Алгоритм ручного рахунку задачі Діріхле.
- •Лабораторна робота №1.
- •Порядок виконання роботи.
- •Контрольні запитання.
- •Деякі узагальнення методу скінченних різниць та його недоліки.
- •7. Різницеві схеми для рівнянь теплопровідності.
- •7.1 Явна різницева схема
- •7.1.1 Алгоритм ручного рахунку
- •7.2 Неявна різницева схема.
- •7.3 Лабораторна робота №2
- •Порядок виконання роботи.
- •Контрольні запитання.
- •8. Різні сімейства різницевих схем для рівняння теплопровідності
- •8.1 Деякі позначення
- •8.2 Різні сімейства різницевих схем для рівняння теплопровідності
- •8.3 Різницеві схеми для рівняння теплопровідності із змінними коефіцієнтами
- •8.4.Різницеві схеми для нелінійного рівняння теплопровідності.
- •9. Монотонні різницеві схеми для рівнянь параболічного типу, що містять перші похідні
- •9.2 Монотонні рс для звичайного рівняння другого порядку, що містить перші похідні
- •9.3 Монотонна різницева схема для параболічного рівняння
- •10. Інтегро-інтерполяційний метод побудови рс.
- •10.1 Вступ. Методи побудови рс
- •10.2 Приклади побудови рс інтегро-інтерполяційним методом.
- •11. Різницеві схеми для рівнянь гіперболічного типу.
- •Різницева схема для рівняння коливання
- •1. Постановка задачі.
- •2. Різницева апроксимація задачі (1)-(3)
- •13. Економічні методи розв’язання крайових задач математичної фізики.
- •13.1 Економічні методи розв’язання першої крайової задачі для двовимірного рівняння теплопровідності.
- •Стійкість поперечно-поздовжньої рс
- •14. Загальні відомості з теорії стійкості рс.
- •1. Канонічний вигляд двохшарових рс.
- •2. Теорема про стійкість по початкових даних
- •Сумарна апроксимація
- •Локальна одновимірна схема Салмарського
- •1. Вступ
- •2. Основна концепція мсе
- •Переваги і недоліки мсе
- •Математичні основи методу мсе
- •Кусково-визначені базисні функції і мсе.
- •Поняття скінченого елемента.
- •V. Питання гарантованого рівня знань
8.3 Різницеві схеми для рівняння теплопровідності із змінними коефіцієнтами
До цього часу ми розглядали різницеві схеми для рівняння теплопровідності із сталими коефіцієнтами.
Розглянемо постановку І-ї крайової задачі для рівняння теплопровідності із змінними коефіцієнтами. Рівняння має вигляд
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
- густина стержня;
- коефіцієнт теплопровідності.
Де
![]() - досить гладкі функції, тобто мають
похідні потрібних порядків по всіх
змінних.
- досить гладкі функції, тобто мають
похідні потрібних порядків по всіх
змінних.
Для
отримання різницевої схеми задачі
(11)-(14) апроксимуємо
![]() його різницевим аналогом є
його різницевим аналогом є
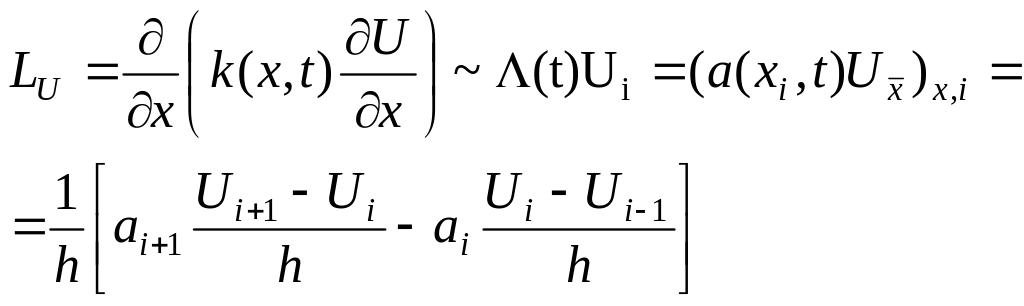 (*)
(*)
![]() -
різницевий коефіцієнт теплопровідності,
який задається умовами другого порядку
апроксимації, а саме
-
різницевий коефіцієнт теплопровідності,
який задається умовами другого порядку
апроксимації, а саме
 (15)
(15)
Для знаходження використаємо:
1.
![]() (16)
(16)
2.
![]() (17)
(17)
3.
![]() (18)
(18)
Тоді для задачі (11)-(14) різницева схема з вагами матиме вигляд:
![]() (19)
(19)
Вигляд
різницевого оператора
![]() має
вигляд (*).
має
вигляд (*).
Висновки:
При маємо явну різницеву схему, тобто
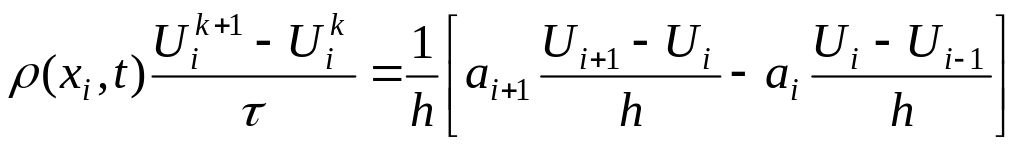 ,
яка легко розв’язується.
,
яка легко розв’язується.При
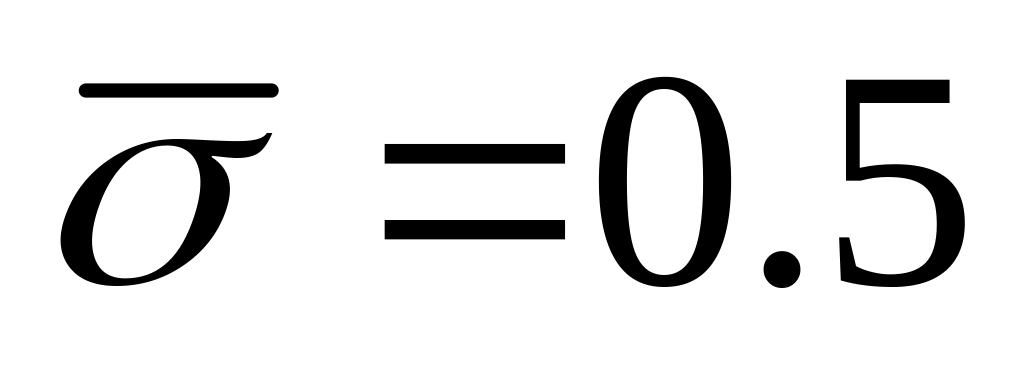 і
і
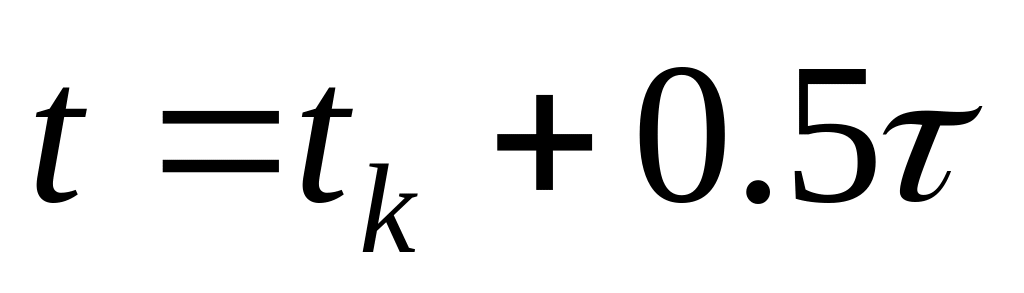 різницева схема має порядок апроксимації
.
різницева схема має порядок апроксимації
.Для всіх інших вона має порядок апроксимації
 .
.
Для дослідження стійкості різницевої схеми із змінними коефіцієнтами застосовується так званий принцип “заморожених коефіцієнтів”.
В другому та третьому випадку для (19)-(22) різницева схема отримується неявною і її розв’язок знаходиться методом прогонки. Для застосування методу прогонки, рівняння (19) потрібно представити в про гоночному вигляді. Для простоти отримаємо ці коефіцієнти при . Тоді рівняння (19) запишеться так
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
Інші коефіцієнти аналогічні попереднім (дивись неявну різницеву схему).
8.4.Різницеві схеми для нелінійного рівняння теплопровідності.
Розглянемо різнецева схема для нелінійного рівняння теплопровідності, тобто рівняння у вигляді:
![]() (31)
(31)
Дане рівняння описує процес поширення тепла у високотемпературній плазмі. У випадку нелінійних рівнянь, коли наперед невідомі межі зміни коефіцієнту теплопровідності K(u), уникають користування явними схемами.
Чисто
неявна різницева схема відносно K(![]() має вигляд:
має вигляд:
![]() ,
де
,
де
![]()
Розв’язок даної різницевої схеми знаходимо методом “прогонки”. Для цього запишемо дану різницеву схему в про гоночному вигляді:

![]()
Часто використовують нелінійну різницева схема
![]()
Коефіцієнт
![]()
Для реалізації цієї схеми потрібно використати той чи інший інтерсхемаційний метод. Наприклад, можна використати такий:
![]() (32)
(32)
Тут s=0,1,2,…,m-1
![]() ;
;
s-номер ітерації
Як
бачимо, нелінійні коефіцієнти беруться
з попередньої ітерації, а в якості
початкового наближення для
![]() вибирається
вибирається
![]() . Це початкове наближення тим краще, чим
менший крок по τ. Число ітерацій m
задається з врахуванням точності. В
задачах з гладкими коефіцієнтами при
K(U)≥c1>0
часто буває достатньо провести дві, три
ітерації. Значення U
на
новій ітерації знаходиться із системи
різницевих рівнянь , методом
’’прогонки’’.
. Це початкове наближення тим краще, чим
менший крок по τ. Число ітерацій m
задається з врахуванням точності. В
задачах з гладкими коефіцієнтами при
K(U)≥c1>0
часто буває достатньо провести дві, три
ітерації. Значення U
на
новій ітерації знаходиться із системи
різницевих рівнянь , методом
’’прогонки’’.
При М=1 даний ітераційний метод співпадає з неявною різницевою схемою.
Для наближеного розв’язання нелінійного рівняння (32) застосовуються також схеми предиктор – коректор другого порядку точності, аналогічний методу Руни-Кутта для звичайного диференціального рівняння. Тут перехід з шару (к) на шар (к+1) здійснюється в два етапи:
K+1

K+½
K
Наведемо приклад такої схеми :
На першому етапі розв’язується неявна різницева схема (лінійна система рівнянь )
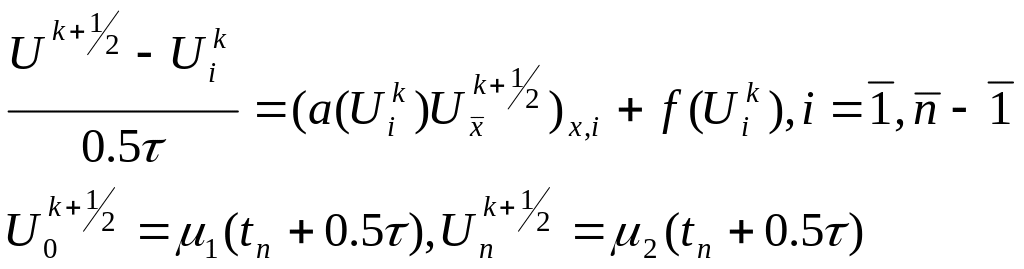
Із якої
знаходяться проміжні значення
![]()
2.Потім,
на другому етапі використовується шести
точкова
схема для рівняння (32), в якому нелінійні
коефіцієнти a(U),
f(U),
![]() і
вона має вигляд:
і
вона має вигляд:
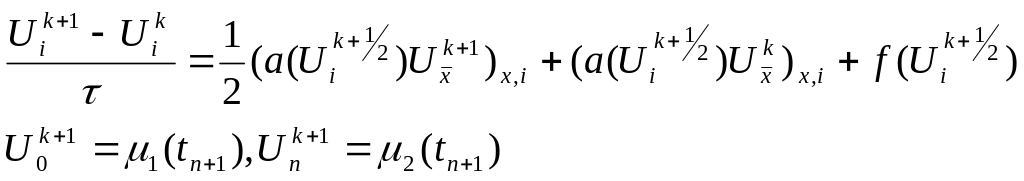
Записуються ці схеми у звичайному вигляді.
