7.2 Неявна різницева схема.

Розглянемо неявну різницеву схему для І-ї краєвої задачі для рівняння теплопровідності.

Як вже зазначалося, явна різницева схема досить проста для розуміння, але володіє істотними недоліками і при чисельних розрахунках прикладних задач спеціалістами в даний час майже не використовується.

По відношенню до стійкості, явну різницеву схему називають умовно стійкою, оскільки вона стійка при певному обмеженні на відношення просторово-часових кроків h і а саме: де В той же час неявні різницеві схеми вільні від таких недоліків.

Як вже відмічалось раніше, неявну різницеву схему отримують шляхом апроксимації (заміни) похідної лівостороньою скінченою різницею по відношенню до вузла ( ), де апроксимують тільки на шарі, тобто шаблон неявної різницевої схеми має вигляд літери “Т” (рис.2.). Отже, після апроксимації похідних , і підставляючи їх в рівняння теплопровідності (2), апроксимуючи початкові і граничні умови (4) отримаємо неявну різницеву схему

Виявляється, що дана неявна різницева схема є стійкою при будь-яких кроках h і і називається абсолютно стійкою. Порядок її апроксимації , тобто перший по і другий – по h. Розв’язок даної схеми знаходиться послідовним обчисленням температури на часових шарах, починаючи з першого ( ). При цьому розв’язок на кожному шарі знаходять методом прогонки, який є однією з модифікацій методу Гаусса розв’язування системи лінійних алгебраїчних рівнянь. В (17) невідомою є температура на шарі, і відомою на -му шарі. Для цього приведемо схему (19) до так званого прогоночного виду:

де ,

Згідно цього методу розв’язок даної різницевої схеми пов’язано з розв’язком СЛАР і набагато важчий ніж розв’язок явної різницевої схеми, але якщо розглянути (20) неважко показати, що матриця буде трьох діагональною. І розв’язок будемо шукати у вигляді

. (22)

Різницева схема (20)-(21) називається неявною різницевою схемою. Розглянемо спеціальні методи розв’язання систем з трьох діагональною матрицею. Цей метод називається методом прогонки. Тут - прогоночні коефіцієнти обчислені на часовому шарі .

Справа в тому, що на кожному часовому шарі приходиться виконувати свою прогонку, тобто розв’язувати СЛАР на кожному шарі по часу. Підставивши (22) в (20), отримаємо:

,

звідси отримаємо

.

Остання рівність можлива лише в тому випадку, коли

,

Звідки знаходимо прогоночні коефіцієнти

, (23)

Щоб обчислити значення про гоночних коефіцієнтів користуючись формулами (23), потрібно мати значення коефіцієнтів , які легко знаходяться із граничних умов (21). Використовуючи (22) і (21) маємо

Таким чином розв’язок неявної різницевої схеми (20)-(21) використовує метод прогонки і він дає формули (22), (23), (25). Для інших краєвид задач розв’язок дається формулами (22), (23), але інші. Тобто маємо

(7.22)

,

В

Рис.7.6. Шаблон обчислення для неявної різницевої схеми.

они обчислюються в результаті прямого ходу (прямої прогонки). В результаті зворотного ходу (зворотної прогонки), обчислюємо по формулі (22) в кожній точці стержня на даному часовому шарі (в певний момент часу).

Зауваження І. На кінцях стержня можуть задаватися різні граничні умови (І-ІІІ роду).

В зв’язку з цим неявна різницева схема (20) – (22) в більш загальному вигляді запишеться так:

де коефіцієнти ₁, ₂, , визначаються тим чи іншим чином в залежності від задання граничних умов І роду, коли задано розподіл температури на кінцях стержня

маємо

для граничних умов ІІ роду, коли на кінцях стержня задано теплові потоки,

(28)

маємо

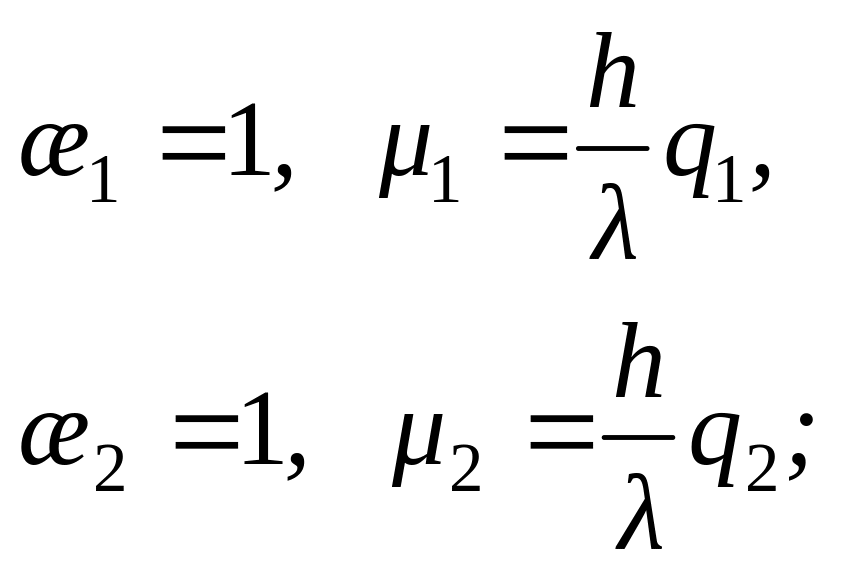
Якщо співставити (27) і (28), то про гоночні коефіцієнти

(30)

Ці формули справедливі для задання будь-яких граничних умов.

для граничних умов ІІІ роду, тобто коли наявний теплообмін між стержнем і навколишнім середовищем

де - температура оточуючого середовища, маємо

(31)

Прогоночні коефіцієнти для всіх випадків граничних умов, обчислюються за формулами (23), причому

(7.23)

У випадку задання граничної умови ІІ або ІІІ роду на правому кінці стержня для проведення прогонки по формулах (22) потрібно знайти температуру . З формул (22) і (20), (27) маємо

Звідки знаходимо :

(32)

Зауваження 2. Для можливості застосування методу прогонки, достатньо, щоб виконувались умови

7.2.1 Алгоритм ручного рахунку по неявній різницевій схемі.

1. Обчислити коефіцієнт температуропровідності

2. Вибрати число поділу відрізка .

3. Обчислити крок розбиття відрізка

4. Вибрати крок по часу та їх кількість m.

5. Обчислити коефіцієнт

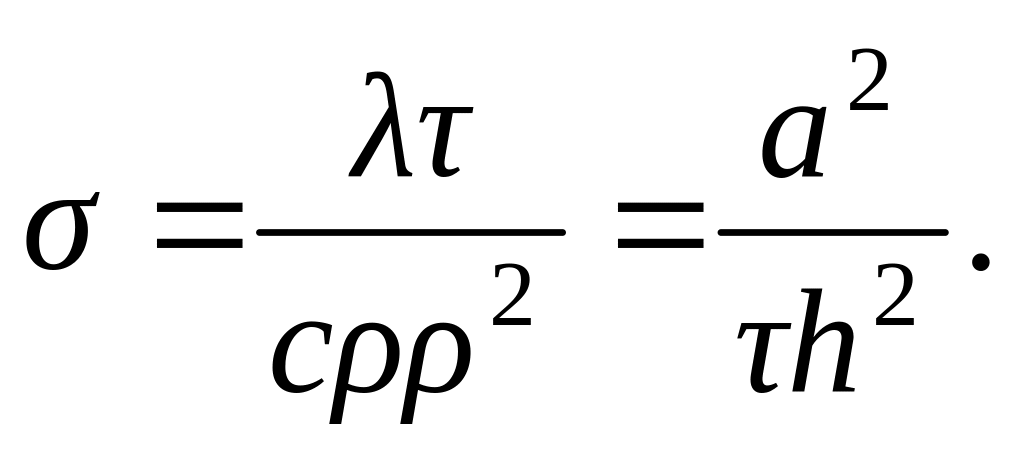
6. Покрити область різницевою сіткою з кроками h і .

7. Користуючись початковою умовою, обчислити

8. Користуючись граничними умовами, обчислити

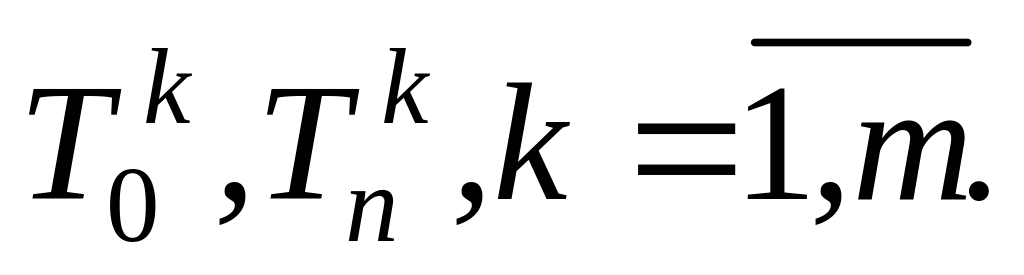
9. Записати неявну різницеву схему задачі.

10. Для кожного часового шару

а) в результаті прямого ходу, обчислити поргоночні коефіцієнти

б) в результаті зворотного ходу, обчислити значення температури

Приклад: Розрахунок розподілу температури в стержні за допомогою неявної різницевої схеми.

Розглянемо умову задачі прикладу 2 поширення тепла в стержні.

Згідно умови, маємо

.

Виберемо крок по часу, наприклад, таким же, як і при застосуванні явної схеми (з метою порівняння результатів по обох різницевих схемах): c.

Обчислення температури будемо проводити для трьох часових шарів (m=3). Параметр , як і раніше, обчислюється так

Початкова і граничні умови такі ж, як і раніше.

Для кожного часового шару k (k=1,2,3) обчислюємо в результаті прямого ходу прогоночні коефіціенти (користуючись формулами (23)), а в результаті зворотного ходу–температуру . Відповідно маємо:

а) для першого часового шару (k=1)

і
1	0	1000	969,017
2	0,12500	857,000	896,14
3	0,12698	797,587	776,13
4	0,12702	698,792	609,01
5	0,12702	558,210	400

Табл. Температура першого часового шару для стержня

б) для другого часового шару (k=2)

i
1	0	1000	962,83
2	0,12500	851,762	888,52
3	0,12698	790,933	788,52
4	0,12702	691,946	602,82
5	0,12702	552,015	400

Табл. Температура другого часового шару для стержня

в) для третього часового шару (k=3)

i
1	0	1000	957,26
2	0,12500	847,115	881,19
3	0,12698	784,538	761,19
4	0,12702	685,335	597,26
5	0,12702	546,457	400

Табл. Температура третього часового шару для стержня.

Обчислені значення температур для кожного часового шару запишемо для наглядності у зведену таблицю.

i j		0	1	2	3	4	5
		0	0,02	0,04	0,06	0,08	0,1
0	0	1000	976	904	784	616	400
1	1	1000	969,017	896,14	776,13	609,01	400
2	2	1000	962,82	888,52	768,52	602,82	400
3	3	1000	957,26	881,19	761,19	597,26	400

Табл. Зведена таблиця розподілу температур у стержні.