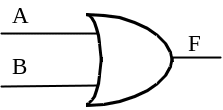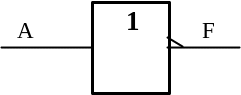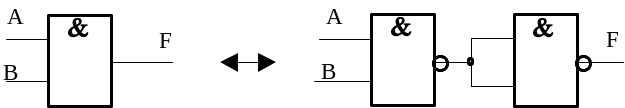- •1. Достоинства и недостатки цифровой электроники
- •2. Двоичные сигналы
- •3. Системы счисления в цифровой электронике
- •4. Алгебра логики
- •4.3. Совершенные нормальные формы (сднф и скнф) записи булевых выражений.
- •4.5. Основные законы булевой алгебры и правила преобразований.
- •4.7. Построение комбинационных логических схем по заданным булевым выражениям.
- •4.8. Особенности построения логических схем
- •7. Транзисторно-транзисторная логика
- •7.2. Состав ттл логических микросхем малой интеграции
- •7.4. Входные каскады ттл микросхем
- •7.5. Статические характеристики ттл микросхем
- •Передаточная характеристика
- •8.1. Инверторы на n–моп и p–моп транзисторах
- •8.2. Инвертор на кмоп транзисторах
- •8.3. Кмоп логические элементы и–не и или –не
- •8.4. Двунаправленный ключ кмоп
- •Разновидности Выходов кмоп микросхем и
- •8.7. Подключение Входов кмоп микросхем
- •9. Эмиттерно–связанная логика.
- •Дополнительная
- •Содержание
4. Алгебра логики
Называемая в честь английского математика Дж. Буля булевой алгеброй, алгебра логики составляет теоретическую основу логики, теории алгоритмов и логического проектирования цифровых схем. От обычной, привычной нам алгебры, булева алгебра отличается тем, что ее логические аргументы (переменные) могут принимать лишь два значения, а основных функций в булевой алгебре всего три: логическое умножение И, логическое сложение ИЛИ и отрицание НЕ.
Два возможных значения логических переменных называют ИСТИНА (TRUE) и ЛОЖЬ (FALSE), иногда их называют ДА и НЕТ, а чаще всего их обозначают соответственно как 1 и 0. При этом следует помнить, что эти логические 0 и 1 не надо трактовать как числа, над ними нельзя производить арифметические действия.
Логическая функция может быть задана четырьмя способами:
1) словесно (описанием ситуации);
2) алгебраическим выражением;
3) таблицей истинности;
4) электрической схемой, состоящей из контактов переключателей.
Например:
1. Лифт можно вызвать, если закрыты двери лифта на первом этаже и на втором этаже и на третьем этаже.
2. Если закрытые двери на первом этаже обозначить как А = 1, на втором как В = 1, на третьем как С = 1, возможность вызвать лифт обозначить как F = 1, а логическую функцию И обозначить знаком умножения "", то алгебраическое выражение будет иметь вид:
F = ABC
3. В таблицу истинности в левой колонке заносятся все возможные комбинации входных аргументов, а в правой колонке записывают соответствующие этим комбинациям значения выходной функции. Входные комбинации записываются в порядке возрастания их значений от всех нулей до всех единиц сверху вниз. Таблица истинности, соответствующая данному примеру будет иметь следующий вид:
А В С F
В С F
––––––––––––––––––
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
4. Электрическая контактная схема обладает хорошей наглядностью, но может быть легко построена лишь для самых простых логических функций. Для нашего примера эта схема может иметь следующий вид:

4.1. ФУНКЦИИ булева базиса И, ИЛИ, НЕ
Наиболее часто встречаются следующие названия и буквенные обозначения функции И: логическое умножение, конъюнкция, совпадение, AND, И.
Возможные виды алгебраической записи функции И:
F = A & B; F = A ^ B; F = A x B; F = A B; F = AB.
Контактная схема для функции И для двух переменных A и B:

Таблица истинности функции 2И:
А В F
В F
––––––––––––
0 0 0
0 1 0
1 0 0
1 1 1
Условное графическое обозначение (УГО) в отечественных схемах логического элемента, реализующего функцию И: |
|
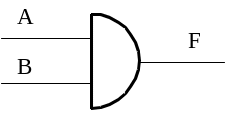
В зарубежных схемах логический элемент И (AND – gate) обозначают следующим образом:
– старое обозначение: |
|
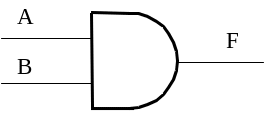
– новое американское обозначение: |
|
– новое европейское обозначение: |
|
Наиболее часто встречаются следующие названия и буквенные обозначения функции ИЛИ: логическое сложение, дизъюнкция, OR, ИЛИ.
Алгебраическая запись функции ИЛИ: F = A v B; F = A + B.
Контактная схема для функции 2ИЛИ:

Таблица истинности функции 2ИЛИ: А В F
––––––––––––
0 0 0
0 1 1
1 0 1
1 1 1
Условное графическое обозначение логического элемента, реализующего функцию ИЛИ в отечественных схемах: |
|
В зарубежных схемах логический элемент ИЛИ (OR – gate) обозначают следующим образом:
– старое обозначение: |
|
– новое американское обозначение: |
|
– новое европейское обозначение: |
|
Наиболее часто встречаются следующие названия и буквенные обозначения функции НЕ: логическое отрицание, инверсия, дополнение, NOT, НЕ.
Возможные виды алгебраической записи функции НЕ:
F = A; F = A , F =A.
Контактная схема для функции НЕ:

Таблица истинности функции НЕ:
А F
F
–––––––
0 1
1 0
Условное графическое обозначение (УГО) логического элемента, реализующего функцию НЕ в отечественных схемах: |
|
В зарубежных схемах логический элемент НЕ (NOT) обозначают следующим образом:
– старое обозначение: |
|
– новое американское обозначение: |
|
– новое европейское обозначение: |
|
4.2. Инвертирующие базисы, ОТРИЦАТЕЛЬНАЯ ЛОГИКА.
Три вышеописанные логические функции И, ИЛИ, НЕ, с помощью которых можно получить все остальные логические функции, называют булевым базисом.
Иногда объединяют две булевы функции (при этом одной из них является НЕ), и получившийся логический элемент считают базовым для получения всех остальных логических функций.
Элемент И–НЕ называют также: штрих Шеффера (Sheffer stroke), NAND (сокращение от NOT AND).
Алгебраическая
запись функции И–НЕ: 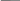 F
= A
B;
F
= A
B.
F
= A
B;
F
= A
B.
Контактная схема для функции И–НЕ для двух переменных A и B:

Таблица истинности функции 2И–НЕ:
А В F
––––––––––––
0 0 1
0 1 1
1 0 1
1 1 0
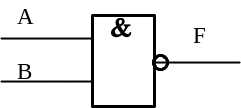
Условное графическое обозначение (УГО) логического элемента, реализующего функцию И–НЕ в отечественных схемах: |
|
В зарубежных схемах логический элемент И–НЕ обозначают следующим образом:
– старое обозначение: |
|
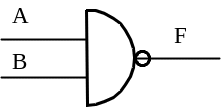
– новое американское обозначение: |
|
– новое европейское обозначение: |
|
Элемент ИЛИ–НЕ называют также: стрелка Пирса (Pierce arrow), NOR (сокращение от NOT OR).
Алгебраическая запись функции ИЛИ–НЕ:

F = A B; F = A + B.
Контактная схема для функции 2ИЛИ–НЕ:

Таблица истинности функции 2ИЛИ–НЕ:
А В F
––––––––––––
0 0 1
0 1 0
1 0 0
1 1 0
Условное графическое обозначение (УГО) логического элемента, реализующего функцию ИЛИ–НЕ в отечественных схемах: |
|
В зарубежных схемах логический элемент ИЛИ–НЕ обозначают следующим образом:
– старое обозначение: |
|
– новое американское обозначение: |
|
– новое европейское обозначение: |
|
Логика называется положительной, если высокий потенциал отображает единицу, а низкий, – ноль. Если наоборот, высокий потенциал отображает ноль, а низкий, – единицу, то логика называется отрицательной. Данное правило называют логическим соглашением.
Самым важным следствием применения отрицательной логики является то, что при переходе от положительной логики к отрицательной функция И превращается в ИЛИ, и наоборот.
Это можно проиллюстрировать следующим образом:
– в положительной логике: в комнате зимой Тепло, если батареи отопления Включены И окна Закрыты ( Т = ВЗ );
– в отрицательной логике: в комнате зимой НЕ Тепло, если батареи отопления НЕ Включены ИЛИ окна НЕ Закрыты ( Т = В + З ).
Здесь И переходит в ИЛИ когда входные аргументы и вывод отрицаются, при этом смысл выражения практически не меняется.
Благодаря этому переходу от И к ИЛИ и удается с помощью однотипных элементов инвертирующего базиса получать все остальные логические функции. Об этом говорят два постулата де 'Моргана:
А
 В
= А
+ В; А
+ В = АВ.
В
= А
+ В; А
+ В = АВ.
Если логический элемент в положительной логике реализует функцию И, то в отрицательной логике этот же элемент реализует функцию ИЛИ, и наоборот, логический элемент ИЛИ положительной логики реализует функцию И в отрицательной логике.
Применение наряду с положительной логикой и отрицательной логики позволяет любое сложное логическое преобразование выполнить с применением только логических элементов И–НЕ или только ИЛИ–НЕ.
Покажем это хотя бы для простейших функций булева базиса.
НЕ |
|
И: |
|
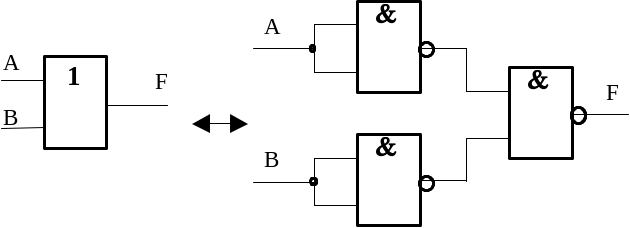
ИЛИ: |
|
Приведенные на этих рисунках построения логических функций НЕ, И, ИЛИ выполнены с помощью только логических элементов 2И–НЕ.