§4 Критериальные уравнения.
В теории подобия при установлении количественных закономерностей оперирует обощенными переменными,роль которых выполняют критерии подобия.
Критерии, в состав которых входят все известные величины (физические), вытекающие из условия однозначности, называется определяющими критериями. Предположим, что мы нашли определенные критерии: K1, K2, K3…..
Критерии, в состав которых входят неизвестные по условию задачи величины, называются неопределяющими критериями: K’ , K”.
Каждый из неопределяющих критериев является однозначной функцией всех определяющих критериев.
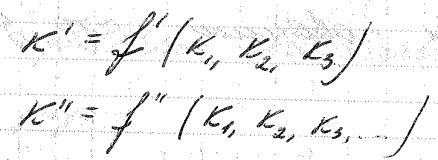
Уравнения, связывающие неопределяющие критерии с определяющими, называется критериальными уравнениями.
Явный вид функции находится из эксперимента. Теория подобия показывает как ставить эксперимент и что необходимо измерять из эксперимента. Ясно видно,что из эксперимента надо определять все величины,которые входят в состав как определяющих,так и неопределяющих критериев.
(полиномы)
Из эксперимента находим показатели степени “n”
Рассмотрим пример:
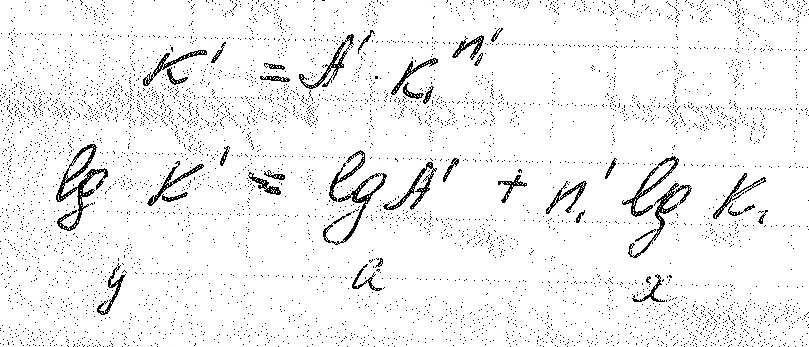
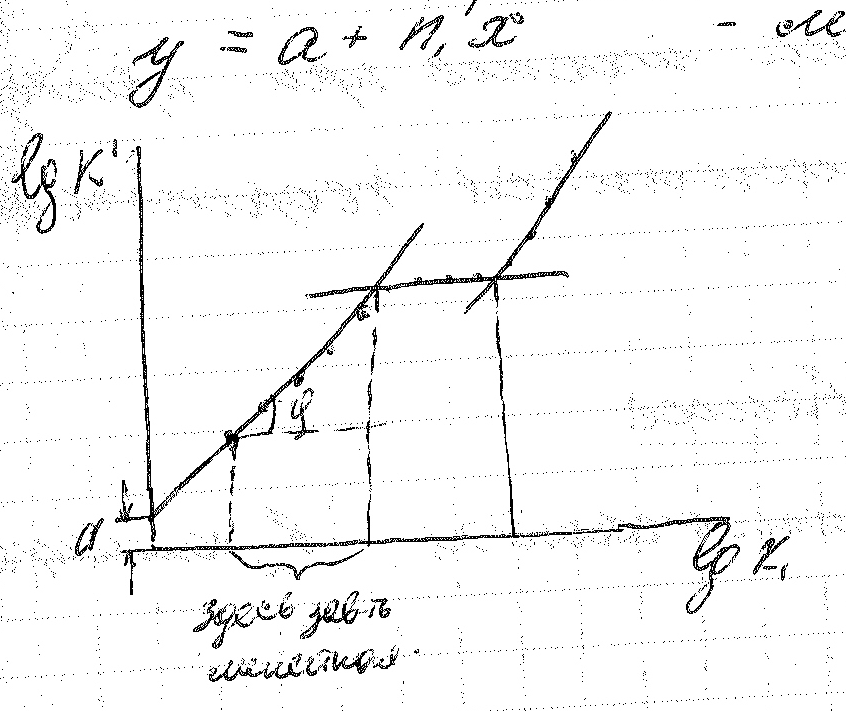
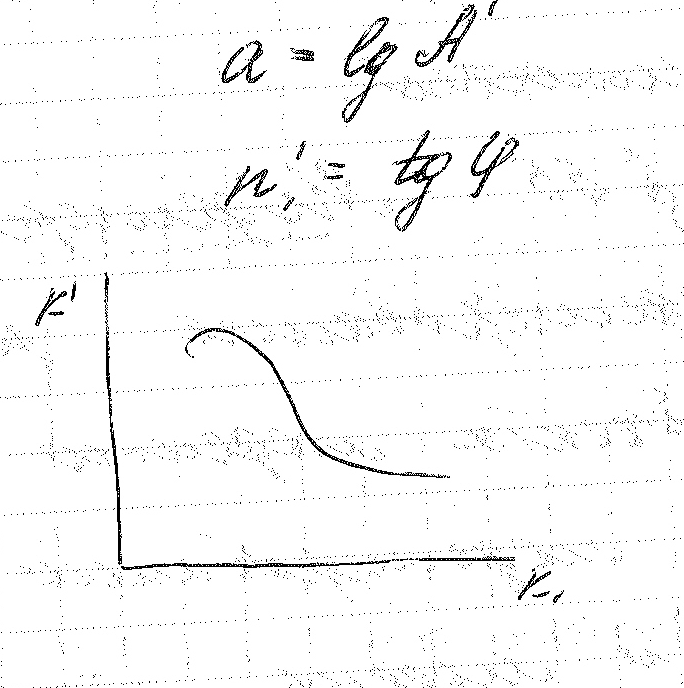
Каждая точка из графика характеризует группу подобных явлений.
Теория подобия дает наиболее плодотворные результаты в том случае, когда задача математически поставлена, но не может быть решена ни теоретическим, ни экспериментальным путем. Она целесообразна также в том случае, когда задача решается экспериментально, но при выборе оптимальных условий приходится затрачивать много времени и средств. Теория подобия удобна также при критериальной обработке имеющихся теоретических зависимостей.
§5 Моделирование.
Моделирование заключается в замещении объекта моделью.
При моделировании необходимо, чтобы и объект и модель относились к одной группе, т.е. отличались между собой только масштабами ( не только геометрическими,но и физическими и т.п.)
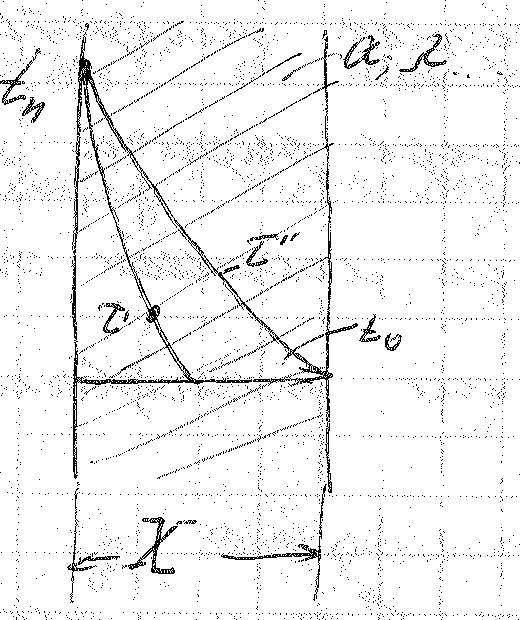
Множитель
преобразования:
,
допустим Kx=0,1.
,
допусти Ка= 1, а – температуропроводимость.
Пусть τ=20
Рассмотрим критерий Фурье, который характеризует температурное поле.
Отсюда:
Тогда:
это получилось по
расчету, тогда как первые два множителя
выбирались производно.Поле жидкости
характеризует критерий Рейпольдса.
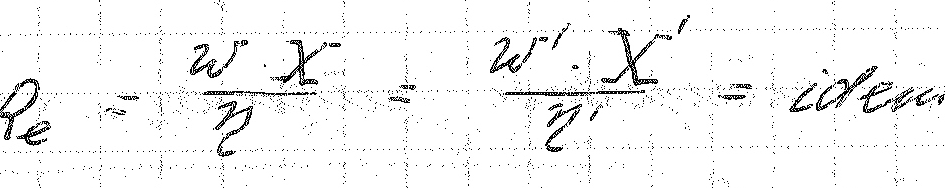
Глава 4. Теплопроводность при стационарном режиме.
Мы должны пользоваться уравнением Фурье:
Условие стационарности:
Отсюда:
,но
Тогда:
-
диф. уравнение теплопроводности Фурье
при стационарном режиме.
§1. Плоская однородная пленка.
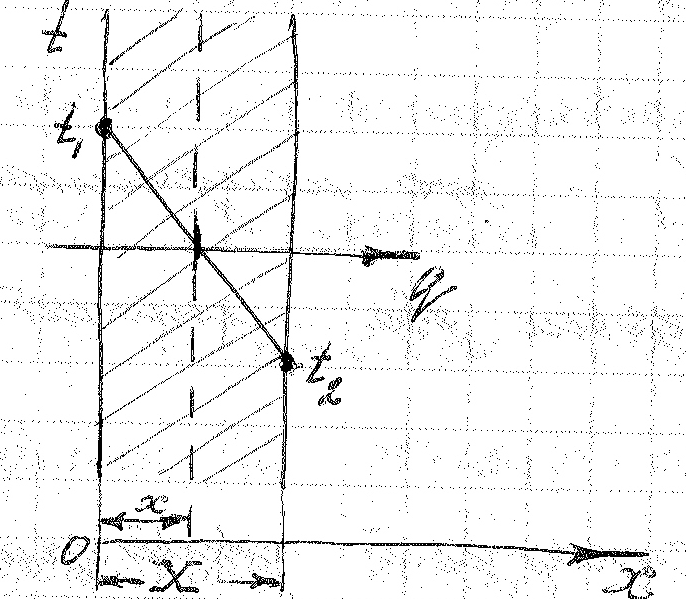Задачи: плоская
стенка имеет толщину X
и неограниченные размеры в других
направлениях, теплопроводность материала
λ.
С одной стороны стенки температура t1, с другой t2. определить распределение температуры по толщине стенки и удельный тепловой поток q, проходящий через стенку, который распространяется только в направлении оси x.
Краткое условие:
Исходное диф. уравнение для решения задачи будет иметь вид:
(«d»
а не «δ» потому что
,
т.е. t
не зависит от времени)
Отсюда:
Разделим переменные:
Отсюда:
Находим C1 и C2 из условий однозначности: при x=0, t=t1, отсюда C2= t,
t = t1+ C1X
при x=X,
t=
t2
и
тогда:
-
это уравнение температурного поля в
плоской стенке.
Выразим это уравнение в обобщенных координатах.
Обобщим:
Тогда получим:
Для определения q выделим изотермическую плоскость в стенке на расстоянии x.
Из уравнения температурного поля видно,что
Поэтому:
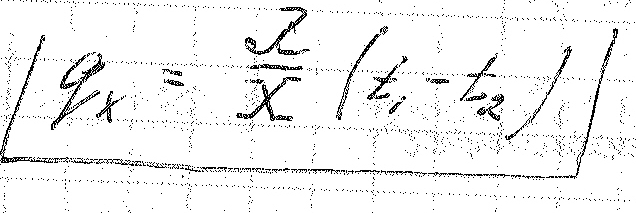
Из уравнения видно, что тепловой поток одинаков по всей толщине стенки (т.к. в правой части нет x).
Тогда можно записать:
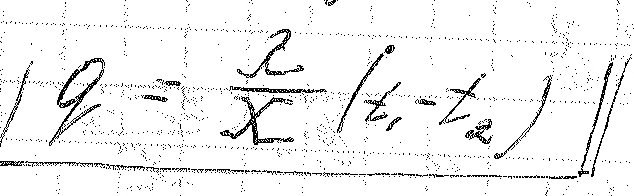
t1- t2 = δt - температурный перепад
-
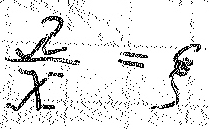тепловая проводимость.
