
- •Глава № 1.Общие понятия и определения.
- •§1. Теплообмен.
- •§2. Температурное поле и температурный градиент.
- •§3 Закон Фурье.
- •§4 Коэффициент теплопроводности.
- •§5 Закон Ньютона
- •Глава 2. Математическая постановка задачи.
- •§1. Дифференциальное уравнение теплопроводности Фурье.
- •§2. Диффиренциальное уравнение движения вязкой несжимаемой жидкости Новье – Стокса.
- •Уравнение сплошности или уравнение неразрывности
- •§ 3 Условие однозначности
- •§4 Методы решения теплофизических задач.
- •Теоретический метод решения задач.
- •Экспериментальный метод.
- •Глава 3. Теория подобия
- •§1 Сущность подобия.
- •§2 Критерий подобия.
- •§3 Метод составления критериев подобия.
- •§4 Критериальные уравнения.
- •§5 Моделирование.
- •Глава 4. Теплопроводность при стационарном режиме.
- •§1. Плоская однородная пленка.
- •§2. Цилиндрическая однородная стенка
- •§3 Плоская многослойная система
- •§4. Теплопроводимость стенки с продольными слоями.
- •§5 Теплопроводимость цилиндрического тела с источниками тепла
- •Глава 5. Теплопередача при стационарном режиме
- •§1 Теплопередача через плоскую стенку
- •§2 Критерий Био (Bi) и его роль при изучении теплообменных процессов
- •Глава 6. Тепловое излучение
- •§1 Основные понятия и определения
- •§2 Основные законы теплового излучения.
- •§3 Лучистый теплообмен между телами
- •Теплообмен между двумя параллельными пластиками.
- •Теплообмен между выпуклым телом и оболочкой.
§5 Закон Ньютона
Часто удельный тепловой поток определяется по формуле:
![]() - уравнение Ньютона.
[Вт/м2]
- уравнение Ньютона.
[Вт/м2]
![]() - тепловая
проводимость производится между
рассматриваемыми т.1 и т.2.
- тепловая
проводимость производится между
рассматриваемыми т.1 и т.2.
![]()
- это количество поверхности тепла, которое проходит через 1 м поверхности за одну секунду при разности температур на границах исследуемого пр-ва в один градус. Эта величина зависит от всего комплекса физических свойств пространства и от процессов, которые протекали в этом пространстве. Задача по определению теплового потока сводится к определению коэффициента . Индекс τ при коэффициенте ξ показывает, что ξ с течением времени изменяется. Если мы не учитывали изменение ξ с изменением времени τ , то тепловую проводимость обозначают просто ξ .
Если идет теплообмен между поверхностью твердого тела и окружающей жидкостью, то вместо ξ пишут α
α - коэффициент теплопередачи ( тепловая проводимость). Δ t= t1-t2- температурный напор.
t1- температура поверхности твердого тела.
t2- температура окружающей жидкости.
К- обозначение тепловой проводимости, когда речь идет о передаче тепла между двумя жидкостями, разделенных твердой стенкой.
К – коэффициент теплопередачи.
Δ t= t1-t2- температурный напор.
Если речь идет о разности температур в твердом теле,то разность температур обозначается δt и называется температурным перенадом
Δt= t1-t2
Величина обратная тепловой проводимости, называется термическим сопротивлением.
![]() -
термическое сопротивление тела.
-
термическое сопротивление тела.
![]() -
термическое сопротивление теплоотдачи
-
термическое сопротивление теплоотдачи
![]() -
термическое сопротивление теплопередачи.
-
термическое сопротивление теплопередачи.
Глава 2. Математическая постановка задачи.
Мы будем стремиться к тому, чтобы определить вид температурного поля
Т= f (x, y, z, τ )
Температура Т – зависимая переменная величина.
x, y, z, τ- независимые переменные велечины.
При математической постановке задачи необходимо на базе основных законов составить уравнение или систему дифференциальных уравнений, которые в дифференциальной форме устанавливают связь между зависимыми и независимыми переменными.
Кроме этого мы должны однозначно определить задачу,т.е. записать условие однозначности. Условие однозначности необходимо для определения постоянных,которые получаются в результате интегрирования дифференциальных уравнений. Диф. уравнения или система диф. уравнений совместно с условиями однозначности представляют математическое решение задачи.
§1. Дифференциальное уравнение теплопроводности Фурье.
Это уравнение связывает в диф. форме температуру с координатами и временем при распространениями тепла путем теплопроводности.
Выводимся это уравнение на базе двух уравнений т.е. двух основных законов закона сохранения энергии и закона Фурье.
Выделим элементарный параллелепипед и возьмем его элементарный объем.
Под элемент объемом понимается такой объем, в котором все физ. Константы по всему объему остаются постоянными во времени распределяются по линейному закону.
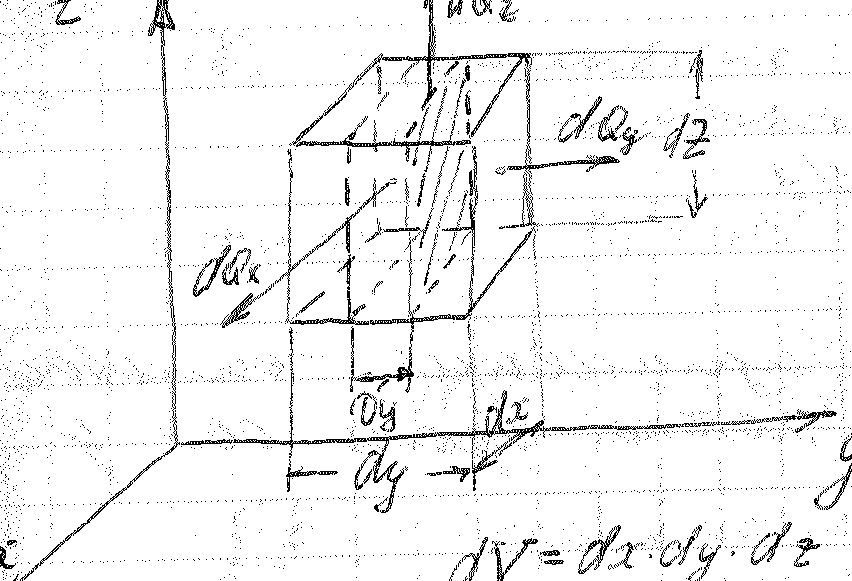
Этот параллелепипед пронизывается тепловым потоком и при прохождении через этот объем тепловой поток меняется на dQ:
dQ=dQx+dQy+dQz
Выделить изотермическую поверхность. Через единицу изотермической поверхности проходит количество тепла.
![]()
Рядом с этой поверхностью выделим еще одну изотермическую поверхность, отстоящую от первой поверхности на расстоянии δy.
δy – это путь, на котором изменяется тепловой поток на δqy.
![]() это изменение
теплового потока на единицу длины.
это изменение
теплового потока на единицу длины.
![]() изменение удельного
теплового потока на длине dy.
изменение удельного
теплового потока на длине dy.
Отсюда:
![]()
![]() изменение теплового
потока оси y.
изменение теплового
потока оси y.
Аналогичного:
![]()
![]()
Просуммируем эти равенства и получили:
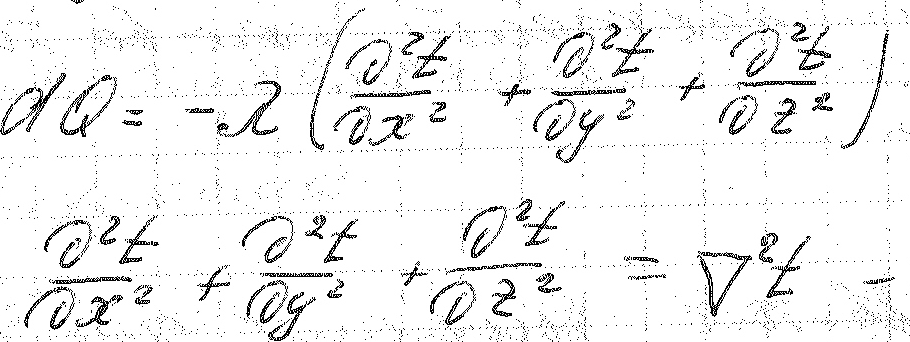 оператор
Лапласса по температуре
оператор
Лапласса по температуре
Тогда:
![]()
С другой стороны в соответствии с законом сохранении энергии. На величину dQ изменяется теплосодержание теплового потока dQ приводит к изменению элемента, теплосодержания тела.
Изменение теплосодержания элемента происходит под влиянием различных факторов.
 -
изменение теплосодержания элемента
под действием изменением температур.
-
изменение теплосодержания элемента
под действием изменением температур.
dQ2 – изменение теплосодержания элемента под влиянием действия источников тепла.
Отсюда:
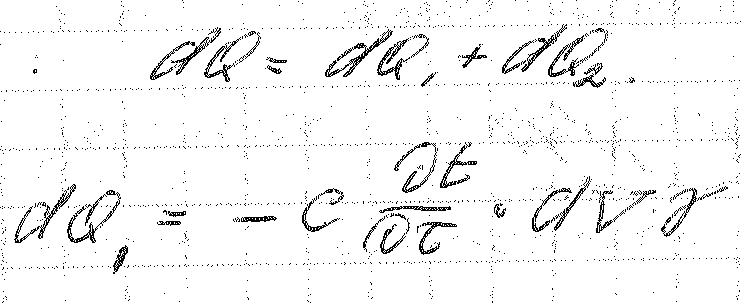 -
изменения теплосодержания всего
параллелепипеда.
-
изменения теплосодержания всего
параллелепипеда.
 -
изменение температуры в единицу времени.
-
изменение температуры в единицу времени.
 -
изменение теплосодержания в единицу
времени.
-
изменение теплосодержания в единицу
времени.
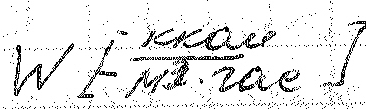 -
мощность источника тепла – это количество
тепла, которое выделяется в единицу
объема за единицу времени.
-
мощность источника тепла – это количество
тепла, которое выделяется в единицу
объема за единицу времени.
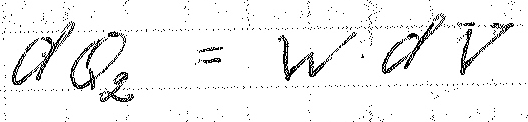
Отсюда:
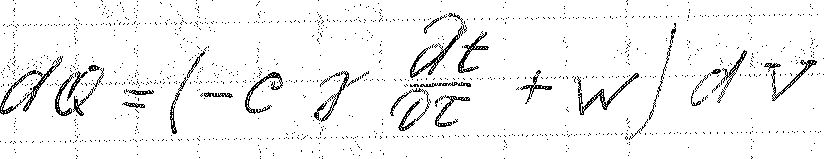
В соответствии с законом сохранения энергии, изменение теплового потока равняется изменению теплосодержания, то:


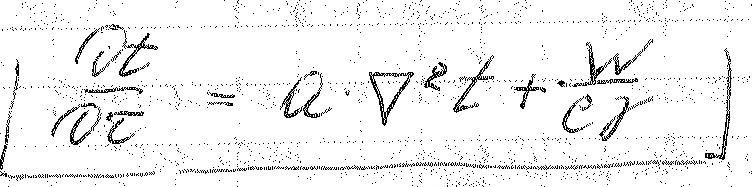 ,где
,где

Это диф. уравнение теплопроводности Фурье с источником тепла. А – коэффициент температуропроводности.
«а» характеризует теплоинерциальные свойства. Иначе «а» характеризует скорость изменения температуры около какой- либо точки.
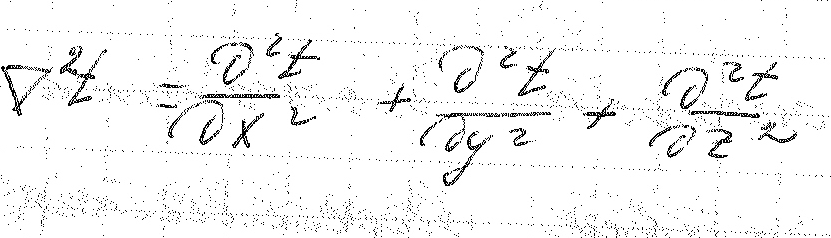 -
в декартовой системе координат.
-
в декартовой системе координат.
Рассмотрим
температурное поле, т.е.
![]()
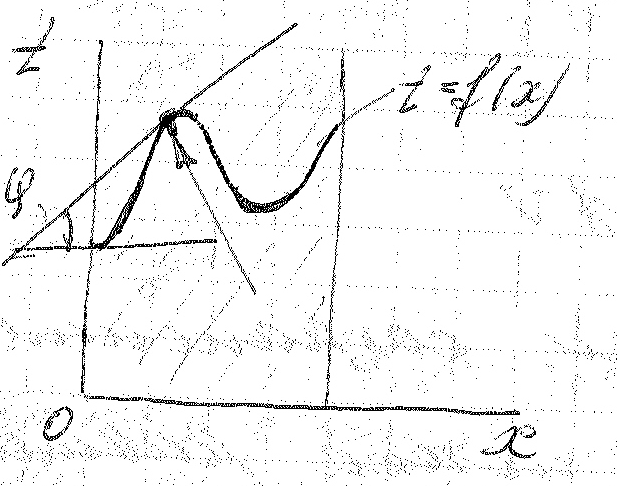

 -
характеризует радиус кривизны,т.е.
кривизну
-
характеризует радиус кривизны,т.е.
кривизну
Оператор Лапласса характеризует кривизну в данной точке.
 -
характеризует скорость изменения
температуры в данной точке. Под влиянием
кривизны температуры поля.
-
характеризует скорость изменения
температуры в данной точке. Под влиянием
кривизны температуры поля.
 -
характеризует скорость изменения
температуры около данной точки под
влиянием источника тепла.
-
характеризует скорость изменения
температуры около данной точки под
влиянием источника тепла.
Диф. уравнение теплопроводности Фурье – это уравнение линейное второго порядка в частичных производных.
Дифференциальные уравнения конвективного теплообмена.
В данном случае
приходится рассматривать
![]() под
действием локальных факторов.
под
действием локальных факторов.
Определим чему равна скорость изменения температуры под действием внешних факторов. За промежуток dr элемент перемещается на величину dx.
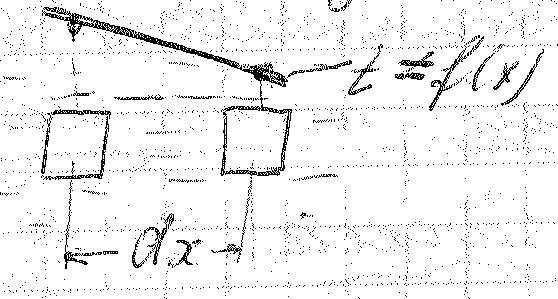
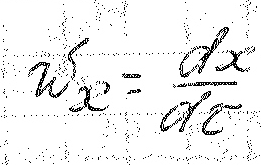 -
скорость движения элемента вдоль оси
x.
-
скорость движения элемента вдоль оси
x.
Чем больше ώx элемента, тем больше скорость изменения температуры под влиянием фактором.
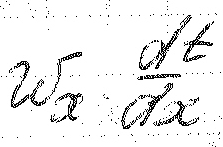 определяют
скорость изменения температуры под
влиянием внешних факторов вдоль оси x.
определяют
скорость изменения температуры под
влиянием внешних факторов вдоль оси x.
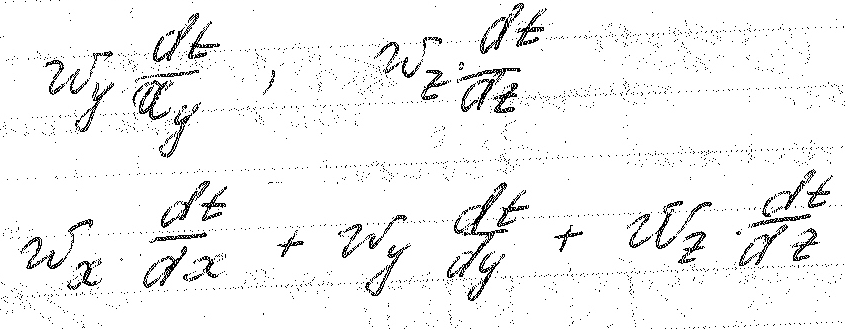 конвективная
составляющая скорости изменения
температуры.
конвективная
составляющая скорости изменения
температуры.
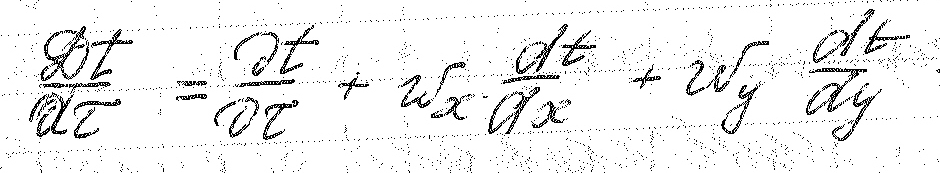

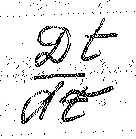 -
субстациональная производная
-
субстациональная производная
 локальная
часть производной
локальная
часть производной
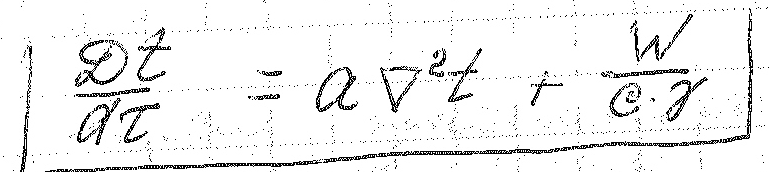 -
диф. уравнение Фурье – Кирхгофа.
-
диф. уравнение Фурье – Кирхгофа.
Это уравнение справедливо, когда
![]()
В отличие от уравнения Фурье в уравнении Фурье – Кирхгофа входят две неизвестные величины: температура t и скорость движения элемента ώ.
