6.Карти Карно

Карта Карно - це спеціального вигляду таблиця, яка дозволяє спростити процес пошуку мінімальних форм і успішно застосовується, коли число змінних не перевершує шести. Карти Карно для функцій, залежних від n змінних, є прямокутник, розділений на 2n кліток. Кожній клітці діаграми ставиться у відповідність двійковий n-мірній набір. Значення заданої функції f з таблиці істинності вносяться до потрібних квадратів, проте якщо клітці відповідає 0, то зазвичай вона залишається порожній.

У першій таблиці показаний приклад розмітки карти Карно для функції, залежної від трьох змінних. Нижні чотири клітки карти відповідають двійковим наборам, в яких змінна x набуває значення 1, чотири верхні клітки відповідають наборам, в яких змінна x набуває значення 0. Чотирьом кліткам складовим праву половину карти, відповідають набори, в яких змінна в; набуває значення 1 і так далі У другій таблиці приведена розмітка карти Карно для n=4 змінних.

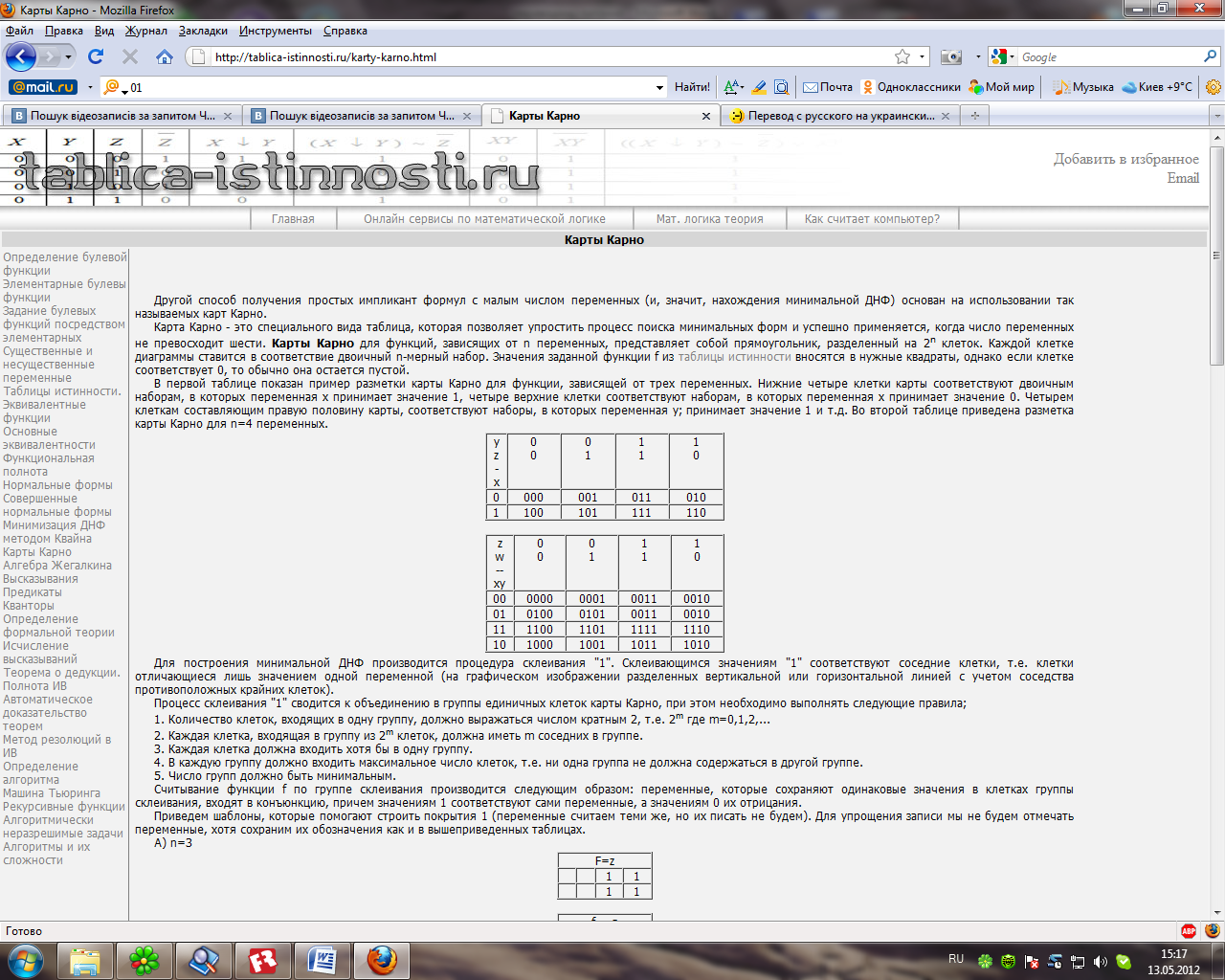
Для побудови мінімальної ДНФ виробляється процедура склеювання "1". Значенням "1", що склеюються, відповідають сусідні клітки, тобто клітки відрізняються лише значенням однієї змінної (на графічному зображенні розділених вертикальною або горизонтальною лінією з врахуванням сусідства протилежних крайніх кліток).

Процес склеювання "1" зводиться до об'єднання в групи одиничних кліток карти Карно, при цьому необхідно виконувати наступні правила:

1. Кількість кліток, що входять до однієї групи, повинна виражатися числом кратним 2, тобто 2m де m=0,1,2...

2. Кожна клітка, що входить до групи з 2m кліток, повинна мати m сусідніх в групі.

3. Кожна клітка повинна входити хоч би до однієї групи.

4. До кожної групи повинне входити максимальне число кліток, тобто жодна група не повинна міститися в іншій групі.

5. Число груп має бути мінімальним.

Призначення

Зазвичай, значні обчислення потрібні для отримання мінімального виду булевої функції, однак карта Карно зменшує потребу таких обчислень завдяки:

• Використанню можливості людского розуму по розпізнаванню шаблонів для визначення які терми мають бути поєднані для отримання найпростішого виразу.

• Дозволяє швидко визначити та видалити потенційні стани гонитв, які неминучі в булевих рівняннях.

• Забезпечує найкращу допомогу в спрощенні до шістьох змінних, однак з більшою кількістю змінних стає складно розрізнити оптимальні шаблони.

• Допомогає в навчанні про булеві функції та їх мінімізацію.

7.Теореми де.Моргана

Англійський математик де Морган (1806—1871) доповнив аксіоми алгебри логіки теоремами, названими в його честь. Теореми де Моргана мають велике практичне значення при спрощенні виразів, що інвертуються, для логічних операцій з елементами І-НЕ і АБО-НЕ. Існують дві теореми де Моргана.

Перша теорема де Моргана:

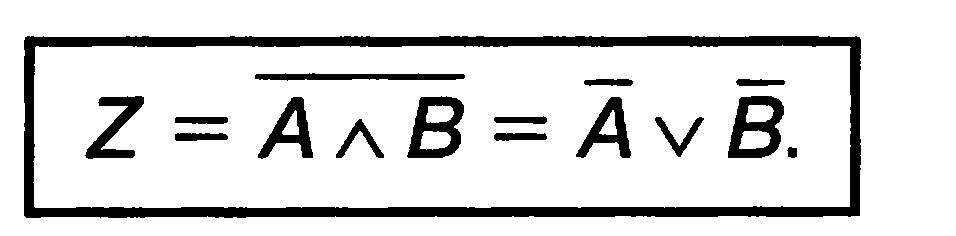
Ця теорема доводиться за допомогою таблиці істинності (мал. 4.17).

Друга теорема де Моргана:

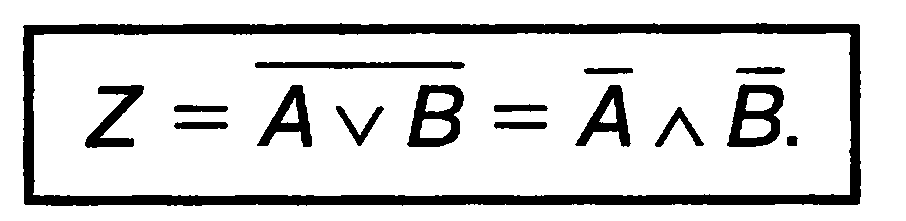
Згідно з теоремами взаємно міняється тип логічної операції (І і АБО). Друга теорема доводиться за допомогою таблиці істинності (мал. 4.18).

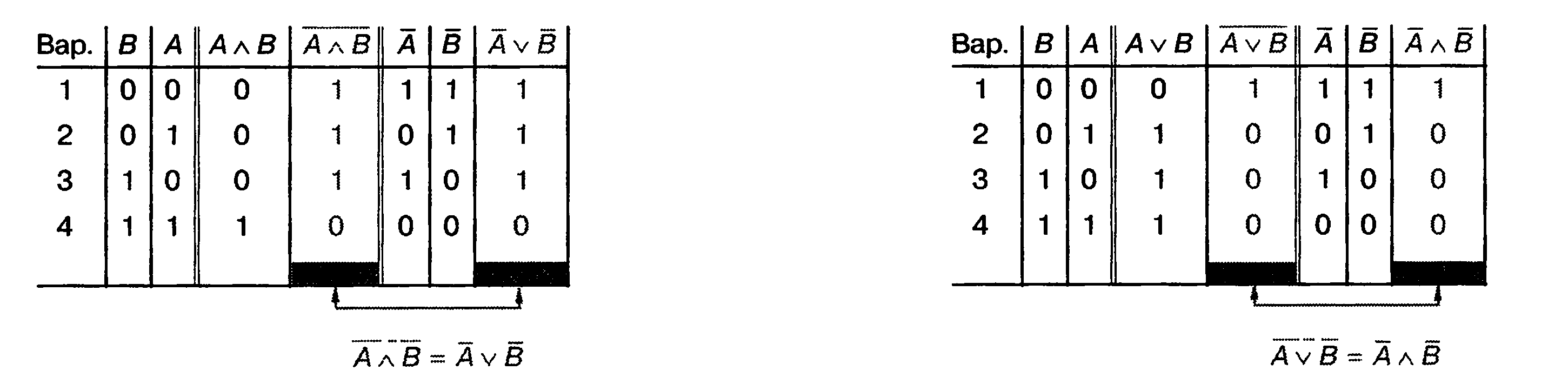
Мал. 4.17. Таблиця істинності для Мал. 4.18. Таблиця істинності для доведення другої теореми Моргана.

доведення першої теореми Моргана.

Покажемо важливість теорем де Моргана на прикладі. З їх допомогою можна значно спростити вираження:

Перша частина рівняння згідно з першою теоремою перетвориться в Друга частина рівняння згідно з тією ж теоремою перетвориться в згідно з аксіомою 9 рівно R

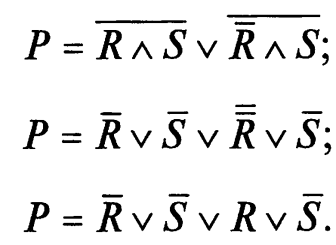
Послідовність змінних по аксіомах 8, 7 і 6: змінена. Проведемо перетворення

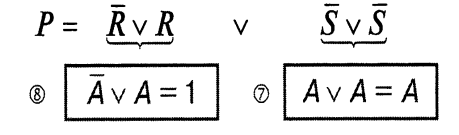
4.3. Аксиомы и тождества алгебры логики

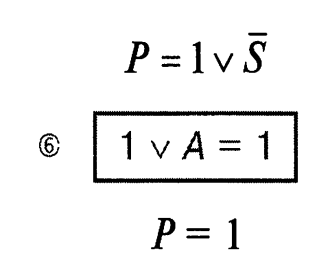
Теореми де Моргана діють також і для логічних операцій з великою кількістю змінних: