
№36 . Асимптоти ф-ції
Асимпто́та криво́ї (грец. ασυμπτωτος — що не збігається, не дотикається) — це пряма, до якої крива при видаленні в нескінченність наближається як завгодно близько.
Якщо крива, задана рівнянням y = f(x), віддаляється в нескінченність при наближення x до скінченної точки a, то пряма x = a називається вертикальною асимптотою цієї кривої.
Такими асимптотами є пряма x = 0 для гіперболи y = 1/x кожна з прямих x = kπ (k = 0, ± 1, ± 2, …) для функції у = ctg(x).
Крім вертикальної асимптоти x = 0 гіпербола y = 1/x має ще й горизонтальну асимптоту у = 0, як і графік функції у = е-x sin(х), проте він, на відміну від гіперболи, перетинає свою горизонтальну асимптоту нескінченну кількість раз (+графік).
Криві, що описуються рівняннями х³ + у³ — Заху = 0 (декартів лист) (+графік), та у = 1/х + х мають похилу асимптоту.
Коефіцієнти
k і b в рівнянні прямої у
= kx + b —
похилої асимптоти кривої у = f(x) при
віддаленні до плюс чи мінус нескінченності,
знаходять як границі:
![]()
Горизонтальна асимптота є частковим випадком похилої при k = 0. Дослідження асимптот дозволяє чіткіше уявити поведінку графіка функції, оскільки властивості функції поблизу її асимптоти дуже близькі до властивостей асимптоти — лінійної функції, властивості якої добре вивчені. Систематичне використання цієї властивості породило напрямок у сучасній математиці — «асимптотичні методи дослідження».
Не всі криві мають асимптоти. Наприклад парабола асимптот не має.
№37. Достатні умови існування екстремуму
Теорема. Нехай є критична точка функції , яка в цій точці є неперервною, і нехай існує окіл точки , в якому має похідну , крім, можливо, точка . Тоді:
1) якщо в інтервалі похідна , а в інтервалі похідна , то є точкою максимуму функції ;
2) якщо в інтервалі , а в інтервалі то є точкою мінімуму функції ;
3) якщо в обох інтервалах і похідна має той самий знак ( набуває або тільки додатних, або тільки від'ємних значень), то не є екстремальною точкою функції .
Перше правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба:
1) знайти стаціонарні точки даної функції (для цього слід розв'язати рівняння , причому з його коренів вибрати тільки дійсні і ті, які є внутрішніми точками області існування функції).
2) знайти точки, в яких похідна не існує (функція в цих точках існує);
3) у кожній критичній точці перевірити зміну знака похідної першого порядку.
Друге правило дослідження функції на екстремум. Щоб дослідити функцію на екстремум, треба знайти:
1) стаціонарні точки заданої функції
2) похідну другого порядку в стаціонарній точці.
3) якщо то в цій точці функція має максимум, якщо мінімум.
№38.Найбільше і найменше значення функції на відрізку.
Щоб знайти найбільше (найменше) значення неперервної функції на відрізку , треба знайти максимуми і мінімуми і порівняти їх із значеннями функції, яких вона набуває на кінцях відрізка. Найбільше (найменше) число серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку .
Приклад. Знайти найбільше і найменше значення функції на відрізку . Р о з в ’я з о к. Знаходимо стаціонарні точки. Для цього обчислимо похідну Прирівнюючи цю похідну до нуля і розв’язуючи рівняння дістаємо стаціонарні точки. Точок, в яких похідна не існує, немає. Обчислимо значення функції в точках (ці точки належать відрізку ), а також на кінцях відрізка, тобто в точках. Маємо Отже, найбільше значення становить , найменше - Щоб знайти найбільше (найменше) значення функції замкненій області , потрібно знайти значення функції у всіх критичних точках і порівняти їх з найбільшими (найменшими) значеннями функції на границях області: найбільше і найменше із цих значень і буде найбільшим і найменшим значенням функції в даній області. Приклад. Знайти найбільше і найменше значення функції в трикутнику (рис. 6.14), обмеженому прямими. Р о з в ’ я з о к. Знайдемо критичні точки функції: Оскільки в даній області, то У критичній точці функція приймає значення Дослідимо поведінку функції на границях області. На прямих і . На прямій ця функція є функцією однієї змінної , оскільки ; Знайдемо найбільше і найменше значення функції на відрізку : Критична точка. В цій точці . На кінцях відрізка. Отже, функція досягає найбільшого значення в точці, а найменшого – в точці. Найбільше значення , найменше значення . Зауваження. До знаходження відповідно найбільшого чи найменшого значення певної функції зводиться цілий ряд практичних задач.
№39.Похідна і диференціали вищих порядків
Розглянемо функцію двох змінних . Її частинні похідні і є функціями змінних і . Від цих похідних також можна знайти частинні похідні. Їх буде чотири, оскільки від кожної з функцій і можна знайти частинні похідні по та по . Назвемо їх частинними похідними другого порядку і позначатимемо:
- функція два рази диференціюється по ;
- функція диференціюється по , а потім по ;
- функція диференціюється по , а потім по ;
- два рази диференціюється по .
Похідні другого порядку також можна диференціювати по і . Одержані при цьому похідні називаються частинними похідними третього порядку функції. Їх буде вісім. Аналогічно позначаються похідні більш високих порядків.
Приклад. Знайти другі частини похідних від функції .
Р о з в ' я з о к. Знайдемо перші частинні похідні:
; .
Диференціюємо кожну з них по і . Одержуємо частинні похідні другого порядку:
.
В розглянутому прикладі
.
Залежність результату диференціювання від порядку диференціювання за різними змінними визначає така теорема.
Теорема. Якщо функція та її частинні похідні означені і неперервні в точці і в деякому її околі, то в цій точці
,
тобто результат диференціювання не залежить від порядку диференціювання за різними змінними.
Доведення теореми опускаємо.
Зауваження. Аналогічна теорема справедлива для будь-якого числа змінних і для похідних більш високих порядків.
Нехай - диференційована в області функція двох незалежних змінних і . В будь-якій точці цієї області ми можемо обчислити новий диференціал:
.
Будемо називати його диференціалом першого порядку. Він залежить від значень і , тобто є функцією чотирьох змінних. Закріпивши і , одержимо функцію двох змінних і , означену в області .
Диференціал від цієї функції в будь-якій точці області , якщо він існує, називається диференціалом другого порядку від функції в точці . Позначається або .
Отже, за означенням .
Аналогічно визначаються диференціали третього, четвертого і т. д. порядків.
№40.Застосування похідної в економіці:граничні показники,еластичність граничних показників.
Економічний зміст похідної. Використання поняття похідної в економіці
Розглянемо задачу про продуктивність праці. Нехай функція и = и(t) відображає кількість виробленої продукції u за час t i необхідно знайти продуктивність праці в момент t0.
За період часу від t0 до t0 + t кількість виробленої продукції зміниться від значення u0 = u(t0) до значення u0 + u = u(t0 +t); тоді середня продуктивність праці за цей період часу zсер=. Очевидно, що продуктивність праці в момент t0 можна визначити як граничне значення середньої продуктивності за період часу від t0 до t0 + t при t à 0 , тобто
Таким чином, продуктивність праці є похідна від обсягу виробленої продукції по часу.
Розглянемо ще одне поняття, яке ілюструє економічний зміст похідної.
Витрати виробництва y будемо розглядати як функцію кількості продукції х, що виробляється. Нехай х — приріст продукції, тоді y — приріст витрат виробництва і - середній приріст витрат виробництва продукції на одиницю продукції. Похідна у' = — виражає граничні витрати виробництва і характеризує наближено додаткові затрати на виробництво одиниці додаткової продукції.
Граничні витрати залежать від рівня виробництва (кількість продукції, що випускається) х і визначаються не постійними виробничими затратами, а лише змінними (на сировину, паливо та ін.). Аналогічним чином можуть бути визначені гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.
Застосування диференціального числення для дослідження економічних об'єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об'єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об'єкта (процесу) за часом або відносно іншого об'єкта дослідження. Але необхідно врахувати, що економіка не завжди дозволяє використовувати граничні величини в силу неподільності багатьох об'єктів економічних розрахунків та перервності (дискретності) економічних показників в часі (наприклад, річних, квартальних, місячних та ін.). Водночас у деяких випадках можна відокремитись від дискретності показників і ефективно використовувати граничні величини.
Для дослідження економічних процесів та вирішення інших прикладних задач використовується поняття еластичності функції.
Означення: Еластичністю функції Еx (y) називається границя відношення відносного приросту функції у до відносного приросту змінної х при х à 0:
Еластичнісіь функції наближено відображає, на скільки відсотків зміниться функція у = f (х) при зміні незалежної змінної х на 1%.
Властивості еластичності функції:
1. Еластичність функції дорівнює добутку незалежної змінної на темп зміни функції Ту = (ln y)’ = , тобто
2. Еластичність добутку (частки) двох функцій дорівнює сумі (різниці) еластичностей цих функцій:
3. Еластичності взаємообернених функцій — взаємообернені величини:
(4.22)
Еластичність функції застосовується при аналізі попиту та пропозиції. Наприклад, еластичність попиту у відносно ціни х (або доходу х) — коефіцієнт, що визначається за формулою (4.21) і наближено відображаючий, на скільки відсотків зміниться попит (обсяг пропозиції) при зміні ціни (або доходу) на 1%.
Економічний зміст частинних похідних
Аналогічно поняттю еластичності функції однієї змінної ми можемо ввести поняття частинних еластичностей функції двох змінних.
№41.Застосування граничного аналізу при розв'язуванні задач оптимізації в економіці. Приклади.
Граничні витрати залежать від рівня виробництва (кількість продукції, що випускається) х і визначаються не постійними виробничими затратами, а лише змінними (на сировину, паливо та ін.). Аналогічним чином можуть бути визначені гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.
Застосування диференціального числення для дослідження економічних об'єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об'єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об'єкта (процесу) за часом або відносно іншого об'єкта дослідження. Але необхідно врахувати, що економіка не завжди дозволяє використовувати граничні величини в силу неподільності багатьох об'єктів економічних розрахунків та перервності (дискретності) економічних показників в часі (наприклад, річних, квартальних, місячних та ін.). Водночас у деяких випадках можна відокремитись від дискретності показників і ефективно використовувати граничні величини.
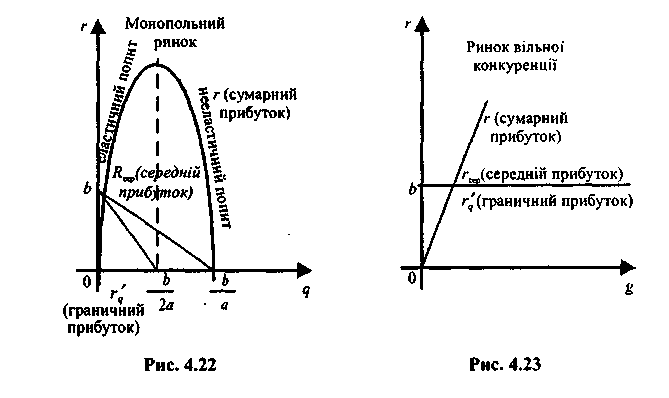
Розглянемо, як приклад, співвідношення між середнім та граничним доходом в умовах монопольного та конкурентного ринків.
Сумарний доход (виручка) від реалізації продукції r можна визначити як добуток ціни одиниці продукції р на кількість продукції q, тобто r = pq.
В умовах монополії
одна або декілька фірм повністю
контролюють пропозицію певної продукції,
а отже і її ціну При цьому, як правило,
зі збільшенням ціни попит на продукцію
падає. Вважаємо, що цей процес проходить
по прямій, тобто крива попиту р
(q)
є лінійна
спадаюча функція p
= aq
+ b
, де
а
< 0, b>0
. Звідси
сумарний доход від реалізованої продукції
складає r
= (aq
+ b)q
= aq2
+bq
(див.
рис. 4.22). В цьому випадку середній
доход на
одиницю продукції rсер
=
![]() , а
граничний прибуток, тобто
додатковий
доход від реалізації одиниці додаткової
продукції, складатиме
, а
граничний прибуток, тобто
додатковий
доход від реалізації одиниці додаткової
продукції, складатиме
![]() (див. рис.
4.22). Звідси, в умовах монопольного ринку
зі зростанням кількості реалізованої
продукції граничний прибуток зменшується,
внаслідок чого відбувається зменшення
(з меншою швидкістю) середнього прибутку.
(див. рис.
4.22). Звідси, в умовах монопольного ринку
зі зростанням кількості реалізованої
продукції граничний прибуток зменшується,
внаслідок чого відбувається зменшення
(з меншою швидкістю) середнього прибутку.
В умовах досконалої
конкуренції, коли на ринку функціонує
велика кількість учасників і кожна
фірма не спроможна контролювати рівень
цін, стабільна реалізація продукції
можлива при домінуючій ринковій ціні,
наприклад, р
= b.
При
цьому сумарний прибуток складатиме r
= bq
i
відповідно середній прибуток rсер
=
![]() ;
граничний прибуток
;
граничний прибуток
![]() (див. рис. 4.23). Таким чином, в умовах ринку
вільної конкуренції, на відміну від
монопольного ринку, середній та
граничний прибутки збігаються.
(див. рис. 4.23). Таким чином, в умовах ринку
вільної конкуренції, на відміну від
монопольного ринку, середній та
граничний прибутки збігаються.
Приклад: Залежність між витратами виробництва у і обсягом продукції х, що випускається, визначається функцією у = 50х - 0,05х3 (грош. од.). Визначити середні та граничні витрати за умови, що обсяг продукції 10 одиниць.
Розв'язок:
Функція середніх витрат (на одиницю
продукції) виражається відношенням
![]() при х =
10 середні витрати (на одиницю продукції)
дорівнюють
при х =
10 середні витрати (на одиницю продукції)
дорівнюють
![]() (грош. од.). Функція граничних витрат
виражається похідною у'(x)
= 50-0,15x2
; при х
= 10
граничні витрати складають у'(10)
= 50-0,15·102
=35 (грош. од.). Отже, якщо середні витрати
на виробництво одиниці продукції
складають 45 грош. од., то граничні витрати,
тобто додаткові затрати на виробництво
додаткової одиниці продукції за
умови даного рівня виробництва (обсягу
продукції, що випускається 10 од.),
складають 35 грош. од.
(грош. од.). Функція граничних витрат
виражається похідною у'(x)
= 50-0,15x2
; при х
= 10
граничні витрати складають у'(10)
= 50-0,15·102
=35 (грош. од.). Отже, якщо середні витрати
на виробництво одиниці продукції
складають 45 грош. од., то граничні витрати,
тобто додаткові затрати на виробництво
додаткової одиниці продукції за
умови даного рівня виробництва (обсягу
продукції, що випускається 10 од.),
складають 35 грош. од.
№42.Область визначення функції багатьох змінних.Інтерпритація в економіці.
Нехай D Rn – довільна множина n-вимірного арифметичного простору. Якщо кожній точці М(х1,…,хn) D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х1,…,хn), то кажуть, що на множині D задана числова функція f : Rn R від n змінних х1…,хn. Множина D називається областю визначення.
Область визначення функції - це множина всіх значень змінної x, при яких функція має зміст.Знайти область визначення деяких функцій, заданих формулою можна:
1. Якщо функція — многочлен, то вона існує при будь-яких значеннях аргумента, тобто її область визначення — всі дійсні числа.
2. Якщо функція задана формулою, яка містить аргумент у знаменнику дробу, то до області визначення функції входять всі дійсні числа, крім тих, які перетворюють знаменник в нуль.
3. Якщо функція задана формулою, яка містить арифметичний квадратний корінь, то до області її визначення входять всі дійсні числа, при яких підкореневий вираз набуває невід'ємних значень.
Одним із базових понять економічної теорії є функція корисності, що
виражає корисність придбання різновидностей товарів. Часто вона
використовується у формах:
- логарифмічна функція;
- функція постійної еластичності.
Функція Кобба - Дугласа - виробнича функція, яка характеризує залежність
об'єму випуску продукції Q від затрат капіталу К і трудових ресурсів.
№43.Частинні похідні.Повна похідна.Повний диференціал і його застосування в наближених обчисленнях.
Частинна похідна функції кількох змінних — це похідна по одній із змінних, причому інші змінні приймаються як аргументи. Часткові похідні використовуються у векторному численні та диференційній геометрії.Часткова похідна функції f за змінною x записується так: fx або ∂f/∂x. Символ часткової похідної ∂ — це заокруглена форма літери d, що використовувалась для запису повної похідної. Позначення було запропоноване Лежандром і стало використовуватись після його представлення в працях Якобі.
Нехай f — функція, що залежить більш ніж від однієї змінної. Наприклад,
f(x,y) = x2 + xy + y2.
Тут f можна інтерпретувати як родину функцій від однієї змінної при заіндексованій іншій:
f(x,y) = fx(y) = x2 + xy + y2.
Іншими словами, при виборі нового значення x утворюється нова функція fx, котра є функцією від одного дійсного аргумента. Тобто,fx(y) = x2 + xy + y2.
Припустимо, що значення x вибрано, покладемо його a, тоді f(x,y) визначає функцію fa, залежну тільки від y: a² + ay + y²:
fa(y) = a2 + ay + y2.
В цьому виразі, a - константа, а не змінна, отже fa - функція від одного дійсного аргумента - y. Відповідно до означення похідної функції одного аргумента:
fa'(y) = a + 2y.
Наведену процедуру можна здійснити для довілього вибору a. Узагальнивши всю сім'ю функцій, отримаємо похідну функції f по змінній y.
Різний вибір індекса a приводить до утворення родини функцій як у наведеному прикладі. Цей приклад також показує, що обчислення часткової похідної, в обчислювальному сенсі, простіше, ніж повної похідної.
Формула носить назву формули повної похідної.
![]() або
або
![]()
Повний диференціал функції f (x, у, z,...) декількох незалежних змінних — вираз
![]()
![]()
У випадку, коли він відрізняється від повного приросту
Δf = f (x + Δx, y + Δy, z + Δz,…) - f (x, y, z, …)
на величину, безкінечно малу на відміну від
![]()
Для того щоб функція в точці була диференційованою, необхідно і достатньо, щоб для неї в цій точці існувала скінчена похідна . При виконанні цієї умови рівність має місце, коли стала дорівнює саме цій похідній. Якщо функція в точці має (скінчену) похідну, то в цій точці функція необхідно неперервна. Для функції двох змінних умова диференційованості жорстокіша, ніж існування частинних похідних в точці.Теорема (необхідна умова диференційованості). Функція диференційована в точці , неперервна в цій точці і має в ній частинні похідні за обома змінними.
№44.Похідна за напрямом. Градієнт функції, його властивості.
Для характеристики зміни скалярного поля в заданому напрямі вводять поняття похідної за напрямом.
Область простору кожній точці М якої
поставлено у відповідність значення
деякої скалярної величини
![]() , називають скалярним полем.
, називають скалярним полем.
Нехай задано скалярне поле
![]() .
Візьмемо в ньому точку
.
Візьмемо в ньому точку![]() і проведемо з цієї точки вектор
і проведемо з цієї точки вектор
![]() , напрямні косинуси якого
, напрямні косинуси якого![]() .
.
На векторі
на відстані
![]() від його початку візьмемо точку
від його початку візьмемо точку![]() .
Тоді
.
Тоді
![]() .
.
Обчислимо тепер приріст![]() функції
при
переході від точки М до точки
функції
при
переході від точки М до точки
![]() в напрямі вектора
:
в напрямі вектора
:
![]() .
.
Перейшовши до границі при
![]() ,дістанемо
формулу для обчислення похідної за
напрямом
,дістанемо
формулу для обчислення похідної за
напрямом
![]()
Фізичний зміст цього результату такий:
зміна напряму на протилежний не впливає
на значення швидкості зміни поля , а
тільки на характер зміни поля . Якщо,
наприклад, в напрямі
поле зростає , то в напрямі
![]() воно спадає , і навпаки .
воно спадає , і навпаки .
Градієнт — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат.
Для скалярного поля
![]() градієнт визначається формулою
градієнт визначається формулою
![]()
Це означення узагальнюється на простори будь-якої розмірності
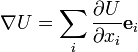
Напрямок, протилежний градієнту, є напрямком найвищого спадання
№45.Лінії і поверхні рівня, їх економічна інтерпретація
Означення 1.Змінна z зветься функцією незалежних змінних х та у, якщо кожній парі (Х,У) з деякої області їх змінювання відповідає певне значення величини z.
Означення2. Лінією рівня функції z=f(x,y) називається множина точок (х,у) площини хОу. В яких функція набуває одного й того самого значення С і визначається співвідношенням f(x,y)=С.
При різних С дістанемо різні лінії рівня для данної функції. Вони утворюють топографічну карту графіка функції f. Якщо вибрати числа С1, С2,………., Сп так, щоб вони утворювали арифметичну прогресію з різницею d, то отримаємо ряд ліній рівня, по взаємномо розміщення яких можна судити про графік функції. Там де лінії розміщуються густіше, функція змінюється швидше, а де рідше – функція змінюється повільніше (поверхня вологіша).
Приклад:
Побудувати графік функції z=х2+у2+1
Візьмемо: z=1, тоді х2+у2+1=1, тобто х2+у2=0 – це точки (0;0); z =2, тоді х2+у2=1 – це коло з центром в початку координат і радіусом 1.
С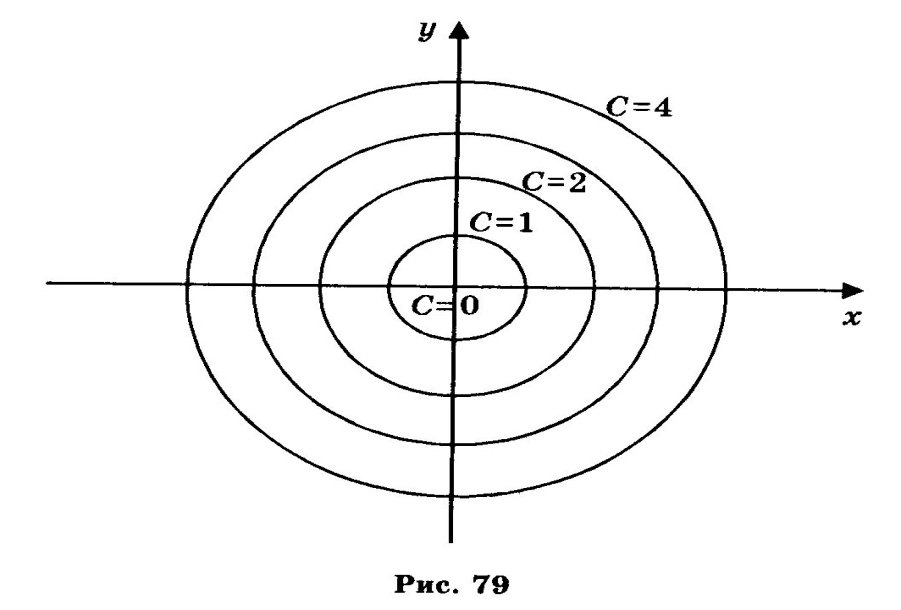
 ім*ю
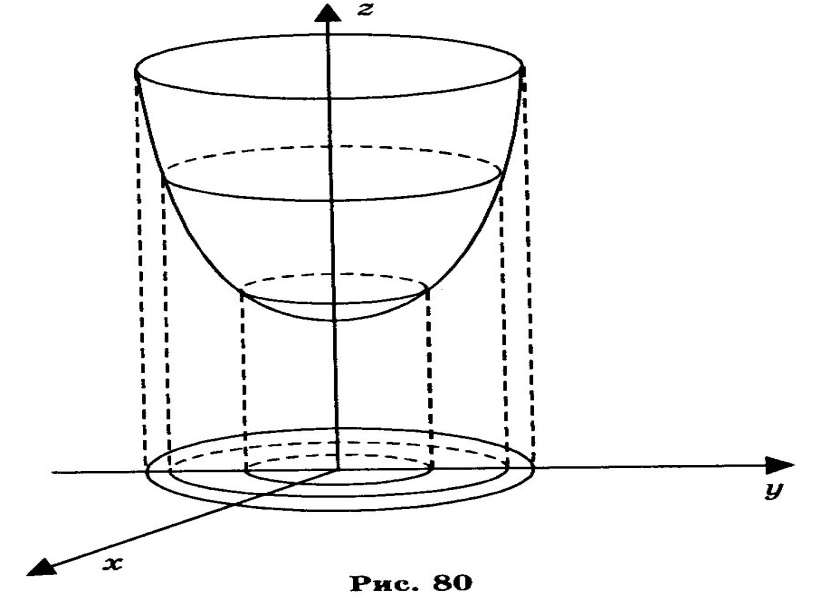
знайдених ліній зображено на малюнку
79. ЯФкщо тепер кожну з ліній розмістити
у відповідній площині, то дістанемо
зображення графіка функції z=х2+у2+1
(мал.80)
ім*ю
знайдених ліній зображено на малюнку
79. ЯФкщо тепер кожну з ліній розмістити
у відповідній площині, то дістанемо
зображення графіка функції z=х2+у2+1
(мал.80)
Відмітимо, що лінії рівня широко використовуються в топографії. На топографічних картах нанесені лінії рівня, відстань між якими постій і дорівнює h. Величина h вказана на карті (наприклад, h=3м.) і дозволяє ефективно використовувати умови місцевості.
