№26.Еліпс, його рівняння.

Еліпсом називається геометричне місце точок, сума відстаней яких до двох фіксованих точок, що називаються фокусами, є величина стала.

Канонічне рівняння еліпса:

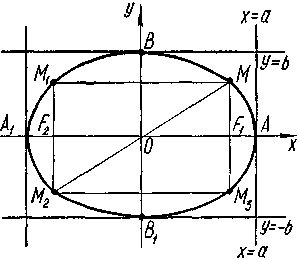
A, A1, B, B1 – вершини еліпса

АА1, ВВ1 – осі еліпса

F1, F2 - фокуси еліпса

№27.Гіпербола, її рівняння.

Гіперболою називається множина точок площини, для яких модуль різниці відстаней від двох фіксованих точок, що називаються фокусами є величина стала і менша відстані між фокусами.

канонічне рівняння гіперболи:

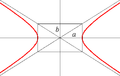
Гіпербола та її фокуси Гіпербола та її напіввіссі та асимптоти.

№28.Парабола, її рівняння.

Параболою називається множина точок площини, кожна з яких знаходиться на однаковій відстані від фіксованої точки, яка називається фокусом, і від фіксованої прямої, яка називається директрисою і не проходить через фокус.

y² = 2px – рівняння параболи.

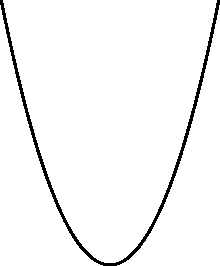
Властивості

Парабола - крива другого порядку.

Вона має вісь симетрії, що називається віссю параболи. Вісь проходить через фокус і перпендикулярна директрисі.

Оптична властивість. Пучок променів, паралельних осі параболи, відбиваючись у параболі, збирається в її фокусі. І навпаки, світло від джерела, що знаходиться у фокусі, відображається параболою в пучок паралельних її осі променів.

Якщо фокус параболи відобразити щодо дотичній, то його образ буде лежати на директрисі.

Парабола є антиподерою прямій.

Всі параболи подібні. Відстань між фокусом і директрисою визначає масштаб.

При обертанні параболи навколо осі симетрії виходить еліптичний параболоїд.

Еволютою параболи є напівкубічна парабола.

№29.Множина. Функції, послідовності, границя послідовностей.

Множина́ — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Наприклад, можна говорити про множину усіх книг в певній бібліотеці, множину літер українського алфавіту або про множину всіх коренів певного рівняння тощо.

Залежність між змінними x та y, в якій кожному значенню змінної x із деякої множини D відповідає єдине значення змінної y, називається функціональною залежністю, або функцією.

Якщо кожному натуральному числу n поставлено у відповідність число хn, то кажуть, що задана послідовність x1, х2, …, хn = {xn}.

Загальний елемент послідовності є функцією від n: xn = f(n).

Число а називається границею послідовності {xn}, якщо для будь- якого додатного >0 існує такий номер N, що для всіх n > N виконується умова:

Позначається: lim xn = a.

Послідовність не може мати більш однієї границі.

Число А називається границею функції f(x) при х→ а, якщо для будь-якого >0 існує таке число >0, що для всіх х таких, що 0 <| x – a| < виконується нерівність

|f(x) – A| < .

Функція f(x) називається нескінченно малою при х→ а, де а може бути числом або однією з величин ∞, +∞ або - ∞, якщо

Функція називається нескінченно великою при х→ а, де а – число або одна з величин ∞, +∞ або -∞ , якщо , де А – число або одна з величин ∞, +∞ або -∞ .

№30.Границя функції.Основні теореми.

Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Теорема 1. Сума (різниця) двох нескінченно малих функцій в даній точці є нескінченно малою функцією в даній точці. Теорема 2. Добуток нескінченно малої функції та обмеженої функції є функцією нескінченно малою в даній точці. Теорема 3. Щоб функція у точці мала границею число A, необхідно і достатньо, щоб різниця була нескінченно малою функцією в цій точці.

Основні теореми про границі функцій

Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому

;

. Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює

Теорема 3. Якщо при функція має границю A, то ця границя єдина.

№31. Похідна функції.Диференціал функції.Геометричний зміст похідної і диференціалу.

Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Нехай функція y = f (x) має в даній точці похідну

тоді

де а 0, якщо х 0.

Помноживши обидві частини на Ах, дістанемо:

Перший з доданків лінійний відносно х і при х 0 та f'(x₀) 0 є нескінченно малою одного порядку з х, тому що:

Другий доданок - нескінченно мала вищого порядку, ніж х, тому що:

Цей доданок не є лінійним відносно х, тобто містить х в степені, вищому від одиниці. Тоді доданок f'(x)· x називається головною частиною суми двох нескінченно малих. У даному випадку це головна частина приросту функції у і називається диференціалом функції. Диференціал функції визначається добутком похідної на приріст незалежної змінної і позначається dy або df(x).

Отже, маємо

dy = f'(x) · x Диференціалом dy називають також диференціал першого порядку. З виразу бачимо що диференціал функції є функція двох незалежних змінних х і х. Якщо y = х, то у' = х' =1, тому dy = dx· x. Тобто диференціал незалежної змінної ототожнюється з її приростом, тобто диференціал незалежної змінної дорівнює приросту незалежної змінної. На цій підставі для будь-якої диференційованої функції y = f (x) можемо формулу записати так:

dy = f' (x) dx Останній вираз називатимемо канонічним виразом диференціала функції y = f (x). З діленням на dх (dх 0), безпосередньо знаходимо:

Виходить, що похідну можна розглядати як відношення двох диференціалів. Тепер у позначенні похідної можемо надавати dy і dx самостійного значення:

Вираз можемо записати ще так:

Звідки

де Якщо х 0, то й отже, і 0. Зауважимо, що коли в точці х₀ похідна то перший доданок f формулі дорівнює нулю і вже не є головною частиною приросту y. Але і в цьому випадку диференціал dy знаходять за формулою.

№32 Основні теореми диференціального числення

1. Теорема РолляТеорема. Нехай функція задовольняє умовам:1) визначена і неперервна на відрізку 2) диференційована в інтервалі ;3) на кінцях відрізка набуває однакових значень: .

Тоді всередині інтервалу  знайдеться хоча б одна точка  в якій .Д о в е д е н н я.Випадок.  Функція  на відрізку  є сталою: . Тоді , тобто в кожній точці похідна дорівнює нулю, а тому за точку можна взяти будь-яку точку інтервалу і для цієї точки теорема буде справедлива. 2. Теорема Лагранжа             Теорема. Якщо функція : 1) задана і неперервна на відрізку; 2) диференційована в інтервалі , то тоді всередині інтервалу  знайдеться хоча б одна точка , в якій справджуються рівність

  Д о в е д е н н я. Розглянемо функцію

,

що задовольняє всім умовам теореми Ролля. Справді,  на відрізку  є неперервною (як різниця двох неперервних функцій), а всередині інтервалу  має похідну

;

.Отже, існує точка  в якій  або, що саме,

звідси