
- •Електронний конспект лекцій з дисципліни «Інтелектуальний аналіз даних»
- •Тема 1. Інтелект як високоорганізована кібернетична система
- •2. Формалізація понять алгоритмічності та декларативності
- •3. Означення інтелектуальної системи
- •Тема 2. Знання як інформаційна основа інтелектуальних систем
- •1. Знання як основа інформаційної системи
- •2. Моделі знань
- •3. Методи інтелектуального аналізу даних
- •1. Знання як основа інформаційної системи
- •2. Моделі знань
- •Тема 3. Концепція інтелектуального аналізу даних.
- •1. Розвиток і призначення дейтамайнінгу (data mining)
- •2. Характеристика процесів і активностей інтелектуального аналізу даних.
- •3. Методи інтелектуального аналізу даних
- •Mineset — візуальний інструмент аналітика
- •2. Характеристика процесів і активностей інтелектуального аналізу даних.
- •3. Методи інтелектуального аналізу даних
- •Збереження даних
- •Дистиляція даних
- •Тема 4. Методи інтелектуального аналізу даних
- •2. Основні етапи та алгоритми інтелектуального аналізу даних
- •3. Огляд алгоритмів та іс Data Mining
- •Тема 5. Особливості статистичного аналізу даних.
- •1. Логіка прикладного статистичного моделювання
- •2. Типи моделей взаємозв’язку. Задача регресії в іад. Сутність і види статистичних прогнозів
- •3. Ідентифікація часових рядів. Аналіз та коригування рівнів часового ряду
- •2.Типи моделей взаємозв’язку. Задача регресії в іад
- •Забезпечення адекватності регресійної моделі
- •2. Сутність і види статистичних прогнозів
- •3. Ідентифікація часових рядів. Перевірка на стаціонарність
- •Тема 6. Перспективні прикладні системи іад
- •2. Орієнтовані на знання системи підтримки прийняття рішень
- •3. Нейронні мережі. Визначення та еволюція нейронних мереж
- •1. Головна їх властивість — здібність до навчання.
- •Застосування нейронних мереж
- •Математична модель біологічного нейрона
- •Математична модель штучного нейрона
- •Загальна схема генетичних алгоритмів
- •Узагальнена схема реалізації генетичного алгоритму
Забезпечення адекватності регресійної моделі
Адекватність регресійної моделі означає здатність її правильно описати реальну структуру взаємозв’язків між ознаками хі та у.
Мірою адекватності моделі слугують відхилення фактичних значень від теоретичних ej = yj – Yj. На величину цих відхилень впливає весь комплекс умов, зокрема:
обсяг та однорідність сукупності;
незалежність спостережень;
інформативність включених у модель факторів;
стабільність не включених у модель факторів;
тип моделі.
Репрезентативність оцінок регресійного аналізу прямо пропорційна обсягу та однорідності сукупності. Саме недостатній обсяг сукупності та її неоднорідність вважаються найвагомішими чинниками неадекватності моделей. Тому при формуванні ознакової множини моделі слід враховувати співвідношення між обсягом вибірки і кількістю включених у модель факторів (воно має бути приблизно 8 : 1).
Інформативність включених у модель факторних ознак залежить як від їх змісту, так і від шкали вимірювання ознаки. Якщо ознака за змістом не інформативна, то ніякий спосіб моделювання не забезпечить належних результатів. Так само результати аналізу будуть суттєво різнитися залежно від того, якою шкалою представлено одну й ту саму ознаку (метричною, ранговою чи номінальною).
Ті властивості, що безпосередньо не вимірюються або не мають єдиного вимірника, включаються в модель у вигляді інтегральних оцінок. Наприклад, погодні умови характеризуються середньодобовою температурою повітря, кількістю опадів, тривалістю сонячного світла, хмарністю і т. ін. Усі ці характеристики агрегуються в індексі погодних умов.
Важливою умовою регресійного аналізу є відсутність мультиколінеарності, яка веде до зсунення оцінок параметрів моделі та унеможливлює коректну інтерпретацію результатів. Два фактори вважаються колінеарними, якщо коефіцієнт кореляції між ними перевищує сукупний коефіцієнт кореляції, тoбто rik > R. Найпростіший спосіб усунення мультиколінеарності — виключити одну із корельованих ознак із моделі або замінити її іншою. Часом колінеарні фактори агрегуються в одну узагальнюючу оцінку.
Стабільність не включених у модель факторів означає, що вплив їх на варіацію у незначний і врівноважується, він однаковий в усіх частинах сукупності (умова гомоскедастичності).
Математичною основою дотримання цих передумов є ймовірнісний розподіл залишків еj. Передбачається, що:
для кожного спостереження залишок еj — випадкова величина, яка має нормальний розподіл. Умова нормальності необхідна для визначення довірчих меж коефіцієнтів регресії і для перевірки гіпотез щодо їх істотності;
математичне сподівання залишків М(е) = 0;
дисперсія залишків однакова в усіх частинах сукупності:
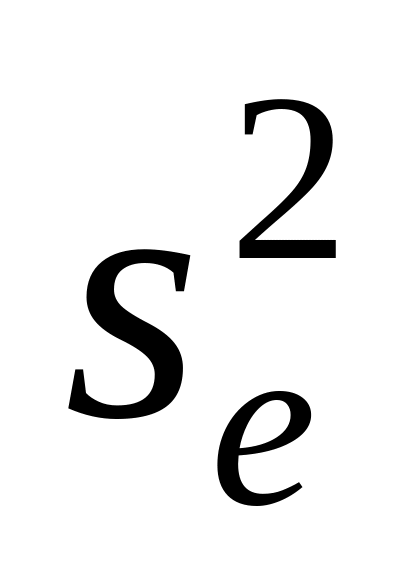 = const.
Ця умова пов’язана з однорідністю
сукупності;
= const.
Ця умова пов’язана з однорідністю
сукупності;залишки незалежні, тобто відсутня серійна кореляція чи автокореляція даних.
2. Сутність і види статистичних прогнозів
Одна з найскладніших проблем системи управління — передбачити майбутнє і знайти ефективні рішення в умовах невизначеності.
Інструментом мінімізації невизначеності слугує прогнозування, а прогнозом називають науково обґрунтований висновок про майбутні події, про перспективи розвитку процесів, про можливі наслідки управлінських рішень.
За специфікою об’єктів прогнозування прогнози поділяють на науково-технічні, економічні, соціальні, військово-політичні тощо.
Економічні прогнози, в свою чергу, класифікують за масштабністю об’єкта на глобальні (світові), макроекономічні, структурні (міжгалузеві та міжрегіональні),
регіональні, галузеві, мікроекономічні.
Прогнозування передбачає систему наукових доведень, використання методів і прийомів з різним ступенем формалізації, узгодженість окремих висновків і оцінок щодо майбутнього розвитку процесу.
В світовій практиці прикладного прогнозування використовують різні методи: статистичні (прогнозна екстраполяція),
функціонально-ієрархічні (прогнозні сценарії),
методи структурної аналогії,
імітаційного моделювання,
експертні оцінки.
Кожен метод має свої особливості, позитивні якості й вади, свої межі використання.
При прогнозуванні соціально-економічних процесів перевага віддається статистичним методам, прогнозним результатом яких є очікувані у майбутньому значення характеристик процесу.
Очевидно, що майбутнє неможливо спостерігати, а очікуваний результат — виміряти, його можна лише передбачити за певних умов, скажімо, «…якщо тенденція не зміниться, то…» або «…якщо станеться подія А, то…» і т. ін. Якщо умови зміняться, то автоматично зміниться й результат прогнозування. Отже, статистичний прогноз, побудований за схемою «…якщо, то…», завжди є умовним.
Іншою особливістю статистичного прогнозу є визначеність його в часі. Часовий горизонт прогнозу називають періодом упередження. За тривалістю цього періоду вирізняють прогнози: короткострокові (до 1 року), середньострокові (до 5 років) і довгострокові (від 5 до 20 років і більше). Тривалість періоду упередження залежить від специфіки об’єкта прогнозування, інтенсивності динаміки, тривалості дії виявлених закономірностей та тенденцій.
Прогнозний результат на період упередження можна представити одним числом (точковий прогноз) або інтервалом значень, до якого з певною ймовірністю належить прогнозна величина (інтервальний прогноз).
Статистичні прогнози ґрунтуються на гіпотезах про стабільність значень величини, що прогнозується; закону її розподілу; взаємозв’язків з іншими величинами тощо. Основний інструмент такого прогнозування — екстраполяція.
Суть прогнозної екстраполяції полягає в поширенні закономірностей, зв’язків і відношень, виявлених в t-му періоді, за його межі. Залежно від гіпотез щодо механізму формування і подальшого розвитку процесу використовуються різні методи прогнозної екстраполяції. Їх можна об’єднати в дві групи:
екстраполяція закономірностей розвитку — тенденцій і коливань;
екстраполяція причинно-наслідкового механізму формування процесу — багатофакторне прогнозування.
Ці методи різняться не процедурою розрахунків прогнозу, а способом описування об’єкта моделювання.
Екстраполяція закономірностей розвитку ґрунтується на вивченні його передісторії, виявленні загальних тенденцій, траєкторій зміни в часі. Абстрагуючись від причин формування процесу, закономірності його розвитку розглядають як функцію часу. Інформаційною базою прогнозування слугують одномірні динамічні ряди.
Важливим етапом статистичного прогнозування є верифікація прогнозів, тобто оцінювання їх точності та обґрунтованості. На етапі верифікації використовують сукупність критеріїв, способів і процедур, які дають можливість оцінити якість прогнозу. Існуючі методи верифікації прогнозів у більшості своїй ґрунтуються на статистичних процедурах, які зводяться до побудови довірчих меж прогнозу, себто до побудови інтервальних прогнозів.
