2.Типи моделей взаємозв’язку. Задача регресії в іад

Усі явища навколишнього світу взаємопов’язані й взаємозумовлені.

Методологічні проблеми побудови моделей взаємозв’язку можна об’єднати в дві групи:

• формування ознакової множини моделі, себто визначення кількості факторів та їх числових еквівалентів;

• модельна специфікація — вибір функціонального виду моделі, ідентифікація та оцінювання параметрів.

При формуванні ознакової множини моделі різноманіт- ні прояви причинно-наслідкових зв’язків доцільно представляти візуально у вигляді спеціальних конструкцій — грфів зв’язку, елементами яких є вершини та орієнтовані ребра (дуги). Вершини графа відповідають ознакам, а дуги по- казують відношення між ознаками.

На рис. 1 показано граф зв’язку чотирьох ознак. За дугами графа можна простежити систему відношень між ними: х впливає на у прямо, безпосередньо, z — прямо та опосередковано двома шляхами: z → х → у та z → v → у. У такій логічній конструкції ознака у є результатом, а х, z і v — факторами, що визначають результат.

Рис. 1. Граф зв’язку

Граф відображує теоретично обґрунтовану систему відношень між ознаками.

Основна мета побудови моделей взаємозв’язку — виявити і кількісно виміряти вплив факторів на результат.

На етапі модельної специфікації враховується характер зв’язку та особливості наявної інформації.

За своїм характером зв’язки поділяються на стохастичні, різновидом яких є кореляційні зв’язки, та жорстко детерміновані (функціональні). Перші відобра­жують стохастичний характер причинно-наслідкових відношень, другі — адитивні чи мультиплікативні зв’язки між елементами розрахункових формул показників.

Відповідно вибирається функціональна форма моделі:

• кореляційні зв’язки описуються переважно регресійними моделями,

• функціональні — балансовими або індексними.

У моделях, що описують функціональні зв’язки, ступінь вільності при формуванні ознакової множини обмежена, маневрувати можна лише кількістю факторів, укрупнюючи їх чи деталізуючи. Для регресійних моделей характерна багатоваріантність як ознакової множини, так і функціональної форми моделі.

Інформаційна база моделі залежить від того, як представлено об’єкт моделювання. Якщо він розглядається як сукупність елементів у просторі, то інформація подається просторовими рядами у вигляді матриці обсягом (n ∙ m), де n — обсяг сукупності, m — кількість включених у модель факторів. Класична регресія передбачає однорідність сукупності, тобто всі одиниці сукупності мають бути однотипними щодо комплексу умов існування, а властиві їм закономірності однаковими для усіх одиниць без винятку.

Регресійна модель описує об’єктивно існуючі між явищами кореляційні зв’язки. За своїм характером кореляційні зв’язки над­звичайно складні та різноманітні. Простежити такі взаємозв’язки і встановити їх точний функціональний вид практично неможливо. Тому при виборі типу функції йдеться лише про апроксимацію відносно простими функціями незрівнянно більш складних за своєю природою взаємозв’язків. Такий підхід, безперечно, є наближеним, містить у собі певну умовність, оскільки передбачає однаковий характер зв’язку з усіма факторами. Проте використання надто складних функцій неминуче веде до збільшення кількості параметрів, а отже, зменшує точність вимірювання та ускладнює інтерпретацію результатів (про це потрібно завжди пам’ятати).

У лінійному щодо параметрів рівнянні регресії індивідуальне значення результативного показника у_j (де j — порядковий номер одиниці сукупності) записується так:

,

де a₀ — вільний член рівняння; економічного змісту, як правило, не має, лише окреслює область існування моделі;

a_і — коефіцієнт регресії; показує, як в середньому змінюється у зі зміною х_і на одиницю її шкали вимірювання за незмінності інших включених в модель факторів і за інших рівних умов;

e_{j =} y_j – Y_j — залишкова величина.

У регресійній моделі основне навантаження покладається на коефіцієнт регресії b_і, він розглядається як своєрідна міра «очищеного» впливу х_і на у і називається ефектом впливу.

Для оцінювання адекватності регресійної моделі використовують:

• стандартне відхилення;

• множинні коефіцієнти детермінації та кореляції;

• частинні коефіцієнти детермінації та кореляції;

• коефіцієнти окремої детермінації;

• критерії перевірки істотності зв’язку.

Стандартне відхилення характеризує варіацію залишкових величин

,

де n — обсяг сукупності, m — кількість коефіцієнтів регресії.

Розрахунок характеристик щільності зв’язку ґрунтується на декомпозиції (розкладанні) дисперсії у за джерелами формування:

,

де — загальна сума квадратів відхилень, зумовлена впливом усіх можливих факторів;

— факторна сума квадратів відхилень, зумовлена впливом включених у модель факторних ознак х_і;

— залишкова сума квадратів відхилень, розмір якої залежить від потужності впливу не включених у модель факторів.

Відношення факторної суми квадратів до загальної характеризує частку варіації у, пов’язану з варіацією включених у модель факторів, і називається множинним коефіцієнтом детермінації

.

За відсутності зв’язку R² ₌ 0. Якщо зв’язок функціональний, то R² ₌ 1. Очевидно, що R² пов’язаний із стандартним відхиленням s_e. При зменшенні s_e значення R² зростатиме і навпаки. Корінь квадратний із коефіцієнта детермінації називають коефіцієнтом кореляції .

Окрім названих множинних коефіцієнтів щільності зв’язку, в комп’ютерних програмах передбачено розрахунок R² з урахуванням числа ступенів вільності:

,

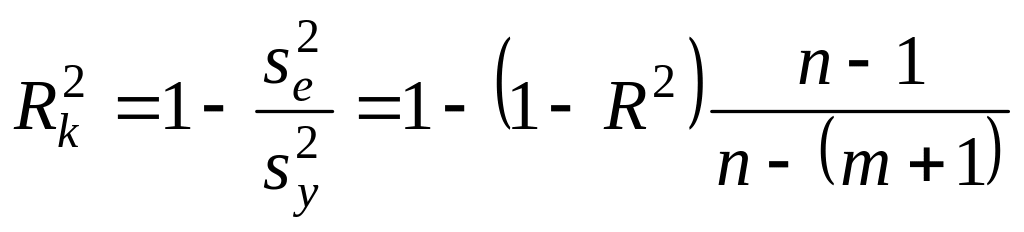де — оцінка дисперсії результативної ознаки у;

— оцінка залишкової дисперсії.

Скоригований коефіцієнт множинної детермінації відрізняється від R² співвідношенням числа ступенів вільності дисперсій: залишкової (n – m + 1) і загальної (n – 1).