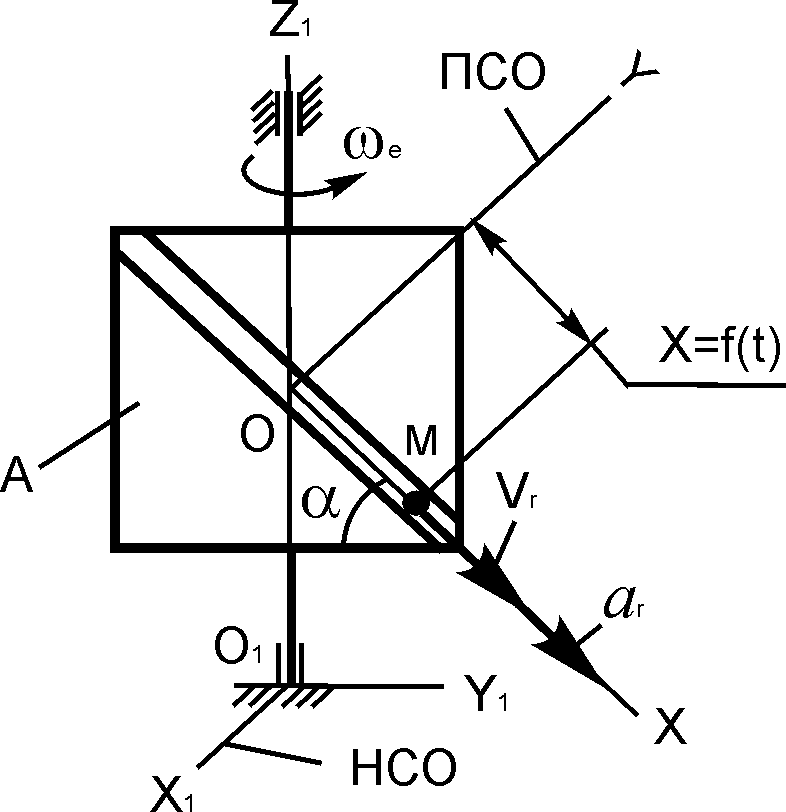
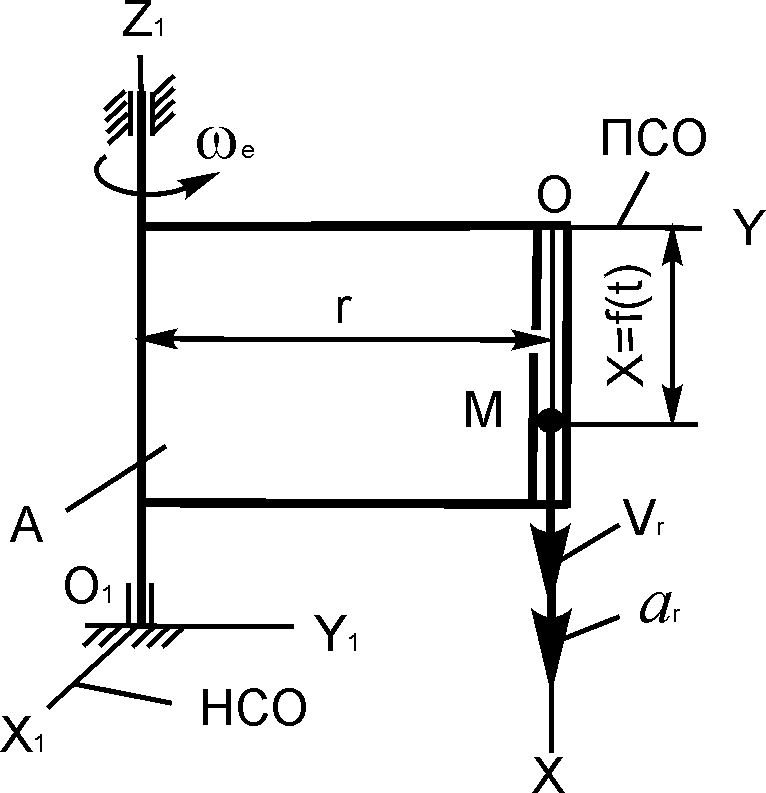
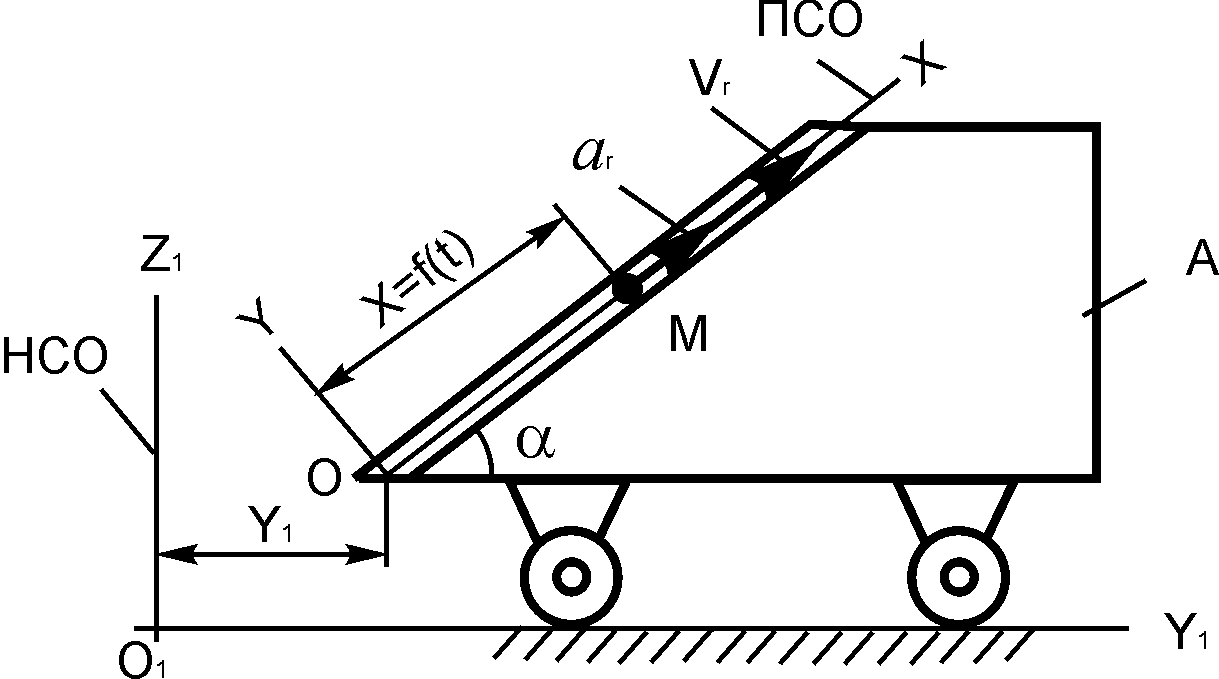
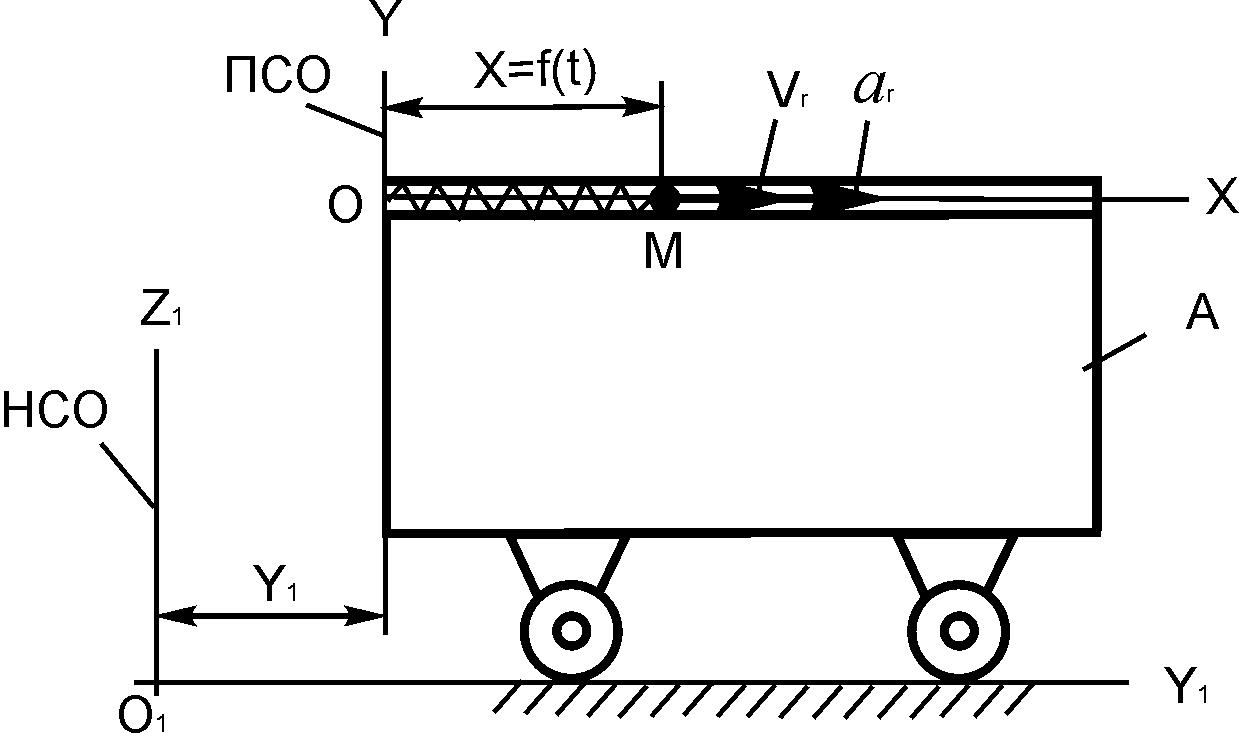
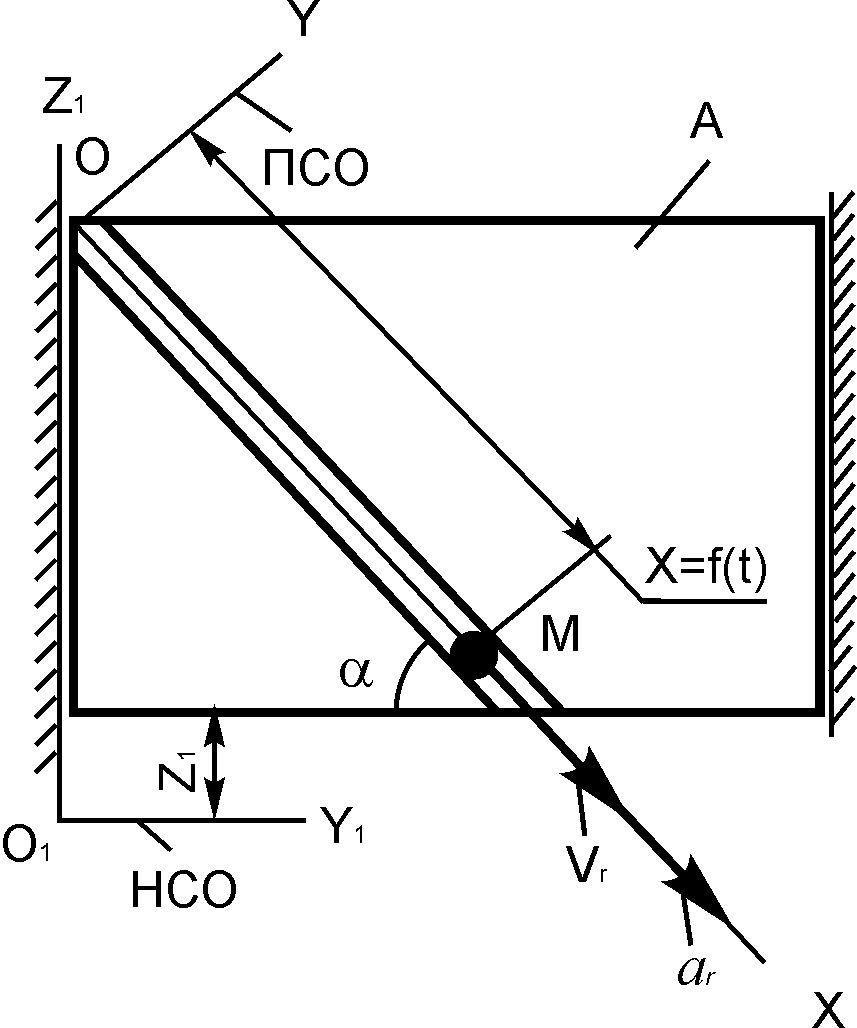
3.5. Варианты курсового задания д 2 «Исследование относительного движения материальной точки»
Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А (табл. 3.1).
Тело А равномерно вращается вокруг неподвижной оси (в вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения O1Z1 вертикальна, в вариантах 1, 12, 15 и 25 ось вращения О1Х1 горизонтальна). В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29 тело А движется поступательно, параллельно вертикальной плоскости O1Y1Z1.
В задании приняты следующие обозначения: m – масса шарика М; ωе – постоянная переносная угловая скорость тела А (в вариантах 1 – 4, 7, 10 – 12, 14, 15, 20, 23, 25, 26, 30); ω – постоянная угловая скорость кривошипов О1В и О2С (в вариантах 6, 17, 22); с – коэффициент жесткости пружины, к которой прикреплен шарик М; l0 – длина недеформированной пружины; f – коэффициент трения скольжения шарика по стенке канала; х0, – начальная координата и проекция начальной скорости на ось ОХ.
Найти уравнение относительного движения этого шарика (x = f(t) = ?), приняв за начало отсчета точку О.
Найти также координату x(t1) и давление шарика на стенку канала N(t1) при заданном значении времени t1. Расчетные схемы рассматриваемых механизмов и данные, необходимые для решения задания, приведены в табл. 3.1.
Таблица 3.1
Номер варианта |
Расчетная схема механизма |
Исходные данные |
1 |
2 |
3 |
1 |
|
m = 0,02 кг; ωe = π рад/с; х0 = 0 м;
t1 = 0,5 c; f = 0
|
2 |
|
m = 0,02 кг; ωe = π рад/с; х0 = 0 м; = 0,2 м/с; t1 = 0,4 c; r = 0,15 м; f = 0
|
3 |
|
α = 45о; m = 0,03 кг; ωe = 2π рад/с; х0 = 0,5 м; = 0 м/с; t1 = 0,2 c; f = 0
|
=
0,4, м/с;
Продолжение табл. 3.1
1 |
2 |
3 |
4 |
|
m = 0,09 кг; ωe = 4π рад/с; х0 = 0,2 м; = – 0,4 м/с; t1 = 0,1 c; с = 0,36 Н/м; l0 = 0,15 м; f = 0
|
5 |
|
α = 60о; m = 0,02 кг; х0 = 0,6 м; = 0 м/с; t1 = 0,2 c; y1 = 0,6–2t3 м; f = 0
|
6 |
|
m = 0,01 кг; ω = 10π рад/с; х0 = 0,5 м; = 0 м/с; t1 = 0,2 c; r = 0,10 м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
7 |
|
m = 0,03 кг; ωе = 2π рад/с; х0 = 0,3 м; = 0 м/с; t1 = 0,2 c; r = 0,20 м; f = 0
|
8 |
|
α = 30о; m = 0,03 кг; х0 = 0,8 м; = 0 м/с; t1 = 0,1 c; z1 = 0,1cos2πt м; f = 0
|
9 |
|
α = 30о; m = 0,02 кг; х0 = 0,4 м; = 0 м/с; c = 0,20 Н/м; l0 = 0,20 м; t1 = 0,1 c; y1 = 4t3 м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
10 |
|
α = 60о; m = 0,05 кг; ωе = 6π рад/с; х0 = 0,4 м; = 0 м/с; t1 = 0,1 c; r = 0,20 м; f = 0
|
11 |
|
α = 30о; m = 0,05 кг; ωе = π рад/с; х0 = 0 м; = 0 м/с; t1 = 0,4 c; f = 0
|
12 |
|
m = 0,08 кг; ωе = 6π рад/с; х0 = 0,05 м; = 0 м/с; t1 = 0,1 c; c = 0,20 Н/м; l0 = 0,10 м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
13 |
|
m = 0,01 кг; х0 = 0 м; = 0,5 м/с; t1 = 0,2 c; z1 = 5–10t2 м; f = 0,1
|
14 |
|
m = 0,05 кг; ωе = 4π рад/с; х0 = 0,5 м; = 0 м/с; t1 = 0,1 c; r = 0,20 м; f = 0,2
|
15 |
|
m = 0,01 кг; ωе = π рад/с; х0 = 0,5 м; = 0 м/с; t1 = 1,0 c; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
16 |
|
α = 45о; m = 0,02 кг; х0 = 1,0 м; = 2,0 м/с; t1 = 0,1 c; y1 = 0,06t3 м; f = 0
|
17 |
|
m = 0,01 кг; ω = 6π рад/с; х0 = 0 м; = 4,0 м/с; t1 = 0,2 c; r = 0,20 м; f = 0
|
18 |
|
α = 40о; m = 0,02 кг; х0 = 0,6 м; = 0 м/с; t1 = 0,1 c; у1 = 0,1sinπt м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
19 |
|
m = 0,08 кг; х0 = 0,4 м; = – 0,8 м/с; t1 = 0,1 c; c = 0,40 Н/м; l0 = 0,20 м; у1 =8t – t3 м; f = 0
|
20 |
|
m = 0,01 кг; ωe = 10π рад/с; х0 = 0,1 м; = 0 м/с; t1 = 0,2 c; с = 0,20 Н/м; l0 = 0,10 м; f = 0
|
21 |
|
α = 30о; m = 0,05 кг; х0 = 0,5 м; = 0,1 м/с; t1 = 0,1 c; у1 =2 + t2 м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
22 |
|
m = 0,03 кг; ω = 4π рад/с; х0 = 0,1 м; = 3,0 м/с; t1 = 0,1 c; r = 0,10 м; f = 0
|
23 |
|
m = 0,01 кг; ωе = π рад/с; х0 = – 0,5 м; = – 0,1 м/с; t1 = 0,2 c; f = 0
|
24 |
|
α = 60о; m = 0,01 кг; х0 = 0 м; = 0,2 м/с; t1 = 0,2 c; у1 = 0,1cos1,5πt м; f = 0
|
Продолжение табл. 3.1
1 |
2 |
3 |
25 |
|
m = 0,05 кг; ωе = 2π рад/с; х0 = 0,1 м; = – 0,4 м/с; t1 = 0,1 c; c = 0,20 Н/м; l0 = 0,20 м; f = 0
|
26 |
|
m = 0,09 кг; ωe = π рад/с; х0 = 0,2 м; = 0,3 м/с; t1 = 0,1 c; с = 0,20 Н/м; l0 = 0,10 м; f = 0
|
27 |
|
α = 75о; m = 0,02 кг; х0 = 1,0 м; = 0,6 м/с; t1 = 0,3 c; z1 = 0,1sin0,5πt м; f = 0
|
Окончание табл. 3.1
1 |
2 |
3 |
28 |
|
m = 0,03 кг; х0 = 0,8 м; = 0 м/с; t1 = 0,3 c; y1 = 8 – 5t3 м; f = 0,1
|
29 |
|
α = 60о; m = 0,10 кг; х0 = 0,4 м; = 1,0 м/с; c = 0,20 Н/м; l0 = 0,20 м; t1 = 0,1 c; y1 = 8 + t3 м; f = 0
|
30 |
|
α = 50о; m = 0,02 кг; ωе = π/2 рад/с; х0 = 0 м; = 0,5 м/с; t1 = 0,2 c; r = 0,50 м; f = 0
|
