2.3. Дифференциальное уравнение движения точки под действием постоянной системы сил, восстанавливающей силы и силы сопротивления движению

Рассмотрим движение материальной точки по гладкой горизонтальной поверхности, происходящее под действием постоянной системы сил, восстанавливающей силы и силы сопротивления движению, пропорциональной первой степени скорости (рис. 2.4).

Как и ранее, начало системы отсчета поместим в положение статического равновесия точки. В этом положении пружина не деформирована, т. е. имеет длину l₀. При оформлении рис. 2.4 используются рекомендации, приведенные в алгоритме решения вторых задач динамики точки.

Основное уравнение динамики в рассматриваемом случае имеет вид

ma = ΣF_i + ΣR_i = G + N + R_c + F_yn,

где G – сила тяжести; N – нормальная реакция; R_c – сила сопротивления движению точки; F_yn – сила упругости пружины.

Рис. 2.4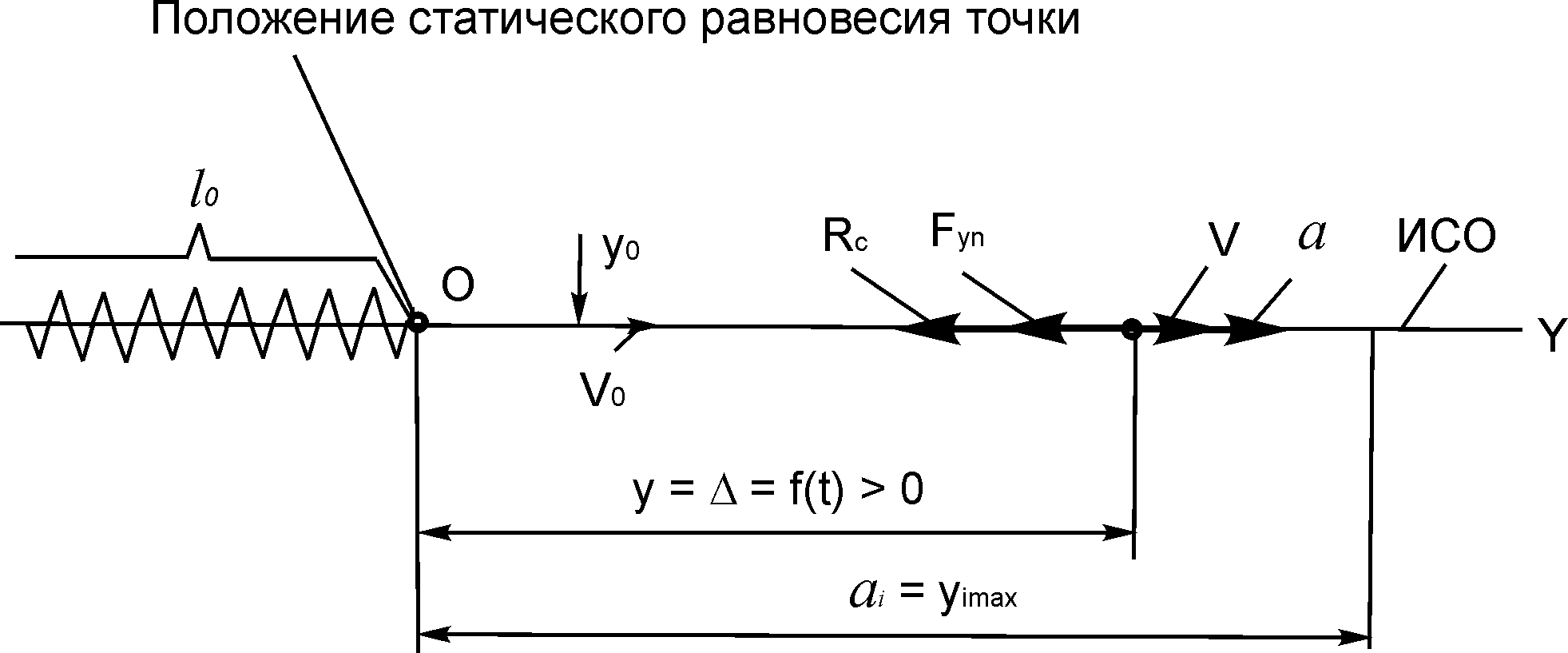

Так как силы G и N на кинематические параметры точки не влияют, то они на рис. 2.4 не показаны.

Сила R_c сопротивления движению точки зависит от внешней среды, в которой эта точка перемещается.

Рассмотрим вариант, при котором сила R_c пропорциональна первой степени скорости V точки. Примером такой силы является сопротивление воздуха при движении тела. В этом случае силу R_c определяют по формуле R_c = – αV, где α – постоянный коэффициент пропорциональности, имеющий размерность [Н/(м/с)]. Коэффициент α численно равен силе сопротивления при скорости движения точки, равной 1 м/с. Сила сопротивления R_c всегда направлена в сторону, противоположную направлению скорости V.

Запишем дифференциальное уравнение горизонтального движения точки:

m = ΣF_ioy + ΣR_ioy = – α – cy.

Это уравнение приведем к виду

+ (α/m) + (c/m)y = 0.

Введем условные обозначения: α/m = 2n; c/m = k². С учетом коэффициентов n, k дифференциальное уравнение движения приводится к стандартному виду:

,

где n – коэффициент, характеризующий сопротивление среды и имеющий размерность [рад/с] или [c^-1].

В зависимости от соотношения величин n и k материальная точка может совершать или колебательное, или апериодическое (неколебательное) движение.

2.4. Затухающие колебания материальной точки

Рассмотрим первый вариант движения точки, при котором n < k. В этом варианте общее решение дифференциального уравнения имеет два вида:

y = e^-nt(C₁cos(( )t) + C₂sin(( )t));

y = ae^-ntsin(( )t + β),

где С₁, С₂, a, β – постоянные интегрирования, определяемые по начальным условиям движения.

Эти выражения называют уравнениями затухающих колебаний материальной точки.

Пусть начальными условиями движения являются: t₀ = 0; y₀; . В этих условиях первый вид решения дифференциального уравнения выражается формулой

y = e^-nt(y₀cos(( )t) + (( +ny₀)/ )sin(( )t)).

Постоянную величину называют циклической частотой затухающих колебаний k^*, которую определяют по формуле

k^* = .

Величина k^* определяет число полных колебаний за промежуток времени, равный 2π = 6,28 с. Тогда имеем

y = e^-nt(y₀cos(k^*t) + (( + ny₀)/k^*)sin(k^*t)).

Как правило, для практических расчетов используют второй вид общего решения дифференциального уравнения движения точки.

y = ae^-ntsin(k^*t + β),

где (k^*t + β) – фаза затухающих колебаний; β – начальная фаза; a – постоянная интегрирования.

Для определения постоянных интегрирования a и β используют следующую совокупность формул:

а = ;

tgβ = y₀k^*/( );

sinβ = y₀/ a;

cosβ = ( )/(аk^*).

Для характеристики затухающих колебаний используют понятие «период затухающих колебаний Т^*».

Период затухающих колебаний – промежуток времени между двумя последовательными прохождениями точки в одном направлении через положение покоя.

Период затухающих колебаний ( = 2π/k^*) больше периода свободных колебаний (T = 2π/k) точки.

Н

Рис. 2.5

а рис. 2.5 приведен общий вид графика затухающих колебаний.

На рис. 2.5 использованы начальные условия движения точки, приведенные на рис. 2.4. График затухающих колебаний располагается в зоне, ограниченной двумя кривыми линиями, описываемыми математическими выражениями: y = аe^-nt; y = – аe^-nt.

Для характеристики затухающих колебаний используют также понятие «амплитуда а_i затухающих колебаний».

Амплитуда затухающих колебаний – величина наибольшего отклонения точки в ту или другую сторону от положения статического равновесия в течение каждого колебания.

Из рис. 2.5 видно, что амплитуда затухающих колебаний переменна. При этом последующая амплитуда а_i+1 меньше предыдущей амплитуды а_i. Это уменьшение характеризуется отношением

а_i+1/ а_i = e^{– nT*/2} = const.

Число e^{– nT*/2} называют декрементом колебаний; натуральный логарифм, т. е. величину nT^*/2, называют логарифмическим декрементом.

Зная предыдущее значение а_i амплитуды, последующее значение а_i+1 находят по формуле

а_i+1 = а_i e^{– nT*/2}.

Следует отметить, что в некоторых учебниках коэффициент n сопротивления среды называют коэффициентом затухания.

Практика показывает, что затухание колебаний происходит очень быстро даже при малом сопротивлении. Так, например, при n = 0,05k имеем Т^*= 1,00125Т, e^–nT* = 0,7301, т. е. период Т^* затухающих колебаний отличается от периода Т свободных колебаний лишь на 0,125 %, а амплитуда а_i за время одного полного колебания уменьшается на 0,27 своей величины, и после 10 полных колебаний становится равной 0,043 своего первоначального значения.

Таким образом, основное влияние сопротивления на свободные колебания материальной точки выражается в уменьшении амплитуды колебаний с течением времени, т. е. в затухании колебаний.

Затухающие колебания называют также колебаниями с малым сопротивлением внешней среды.