
- •Описательная статистика. Основные понятия биометрии
- •Основные характеристики статистических совокупностей. Средние величины и показатели вариации. Квантили и выбросы
- •Квантили.
- •Вариационные ряды. Построение интервального ряда
- •Случайные величины и их распределение
- •Оценки. Статистические ошибки
- •Статистика выводов
- •Критерии достоверности оценок. Статистические гипотезы, их проверка
- •Асимметрия и эксцесс.
- •Непараметрические критерии
- •Первичная статистическая обработка экспериментальных данных
Квантили.
К структурным характеристикам вариационного ряда относятся квантили, отсекающие в пределах ряда определенную часть его членов (вариант). К ним относятся квартили (quartiles), децили и перцентили (percentile) (процентили). Квартиль – величина, отсекающая ¼ всех членов ряда. Три квартиля – q1, q2, q3 – делят весь вариационный ряд на четыре равночисленные части (кварты). Дециль – величина, отделяющая ¹/10 всех членов ряда. Девять децилей делят весь вариационный ряд на десять равных частей. Соответственно, перцентиль (процентиль) (Pi) – величина, отделяющая ¹/100 всех членов ряда. Девяносто девять перцентилей делят весь вариационный ряд на сто равных частей. В практике используются обычно перцентили: P3, P10, P25, P50, P75, P90, P97, причем P50 равен медиане, второму квартилю q2 и пятому децилю данного распределения. Между P25 и P75 и соответственно между q1 и q3 находится 50% всех членов совокупности (P25 = q1 и P75 = q3), этот интервал называется интерквартильный диапазон (IQR).
Выбросы.
Характеристики распределений могут существенно зависеть от экстремальных, резко выделяющихся значений - выбросов. Выбросы могут иметь очень большие или очень маленькие значения, могут быть абсолютно не связаны с остальными данными или не соответствовать свойствам распределения. Выбросы возникают либо из-за ошибок ввода, либо в результате необычного или уникального события. Выброс ни в коем случае нельзя исключать из анализа только потому, что он имеет экстремальное значение, его необходимо тщательно проанализировать. В этом случае выполняют 2 вида анализа: с выбросами и без них. Если сделанные выводы остались неизменными, то такие выбросы не имеют большого значения. А если существенно различаются, необходимо найти объяснение расхождениям. Для определения типа выброса необходимо знать интерквартильный диапазон (IQR) выборки, который находится между 1 и 3 квартилями. Если значение больше 3 квартиля плюс 1,5*IQR или меньше 1 квартиля минус 1,5* IQR, то оно называется умеренным выбросом. Если значение больше 3 квартиля плюс 3* IQR или меньше 1 квартиля минус 3*IQR, то оно называется экстремальным выбросом.
Иногда применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 СКО (и даже ±1.5 СКО) от выборочного среднего. В ряде случаев такая «чистка» данных абсолютно необходима.
Наиболее точно можно отличить выброс от экстремального значения и решить вопрос об исключении варианты из анализа с помощью сравнения фактически определенного нормированного отклонения с табличным значением. Если посчитанное значение больше табличного – сомнительную варианту отвергают, если нет – оставляют для проведения анализа.
Вариационные ряды. Построение интервального ряда
Вариационные ряды принято изображать в виде графиков. При построении графика по оси абсцисс откладывают значения вариант, по оси ординат — их частоты. В результате получается так называемая гистограмма распределения частот. Соединяя вершины перпендикуляров прямыми линиями, получают геометрическую фигуру в виде многоугольника называемую полигоном распределения частот. Линия, соединяющая вершины перпендикуляров, называется вариационной кривой или кривой распределения частот вариационного ряда.
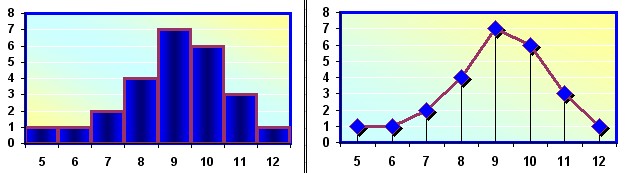
В зависимости от того, как варьирует признак – дискретно или непрерывно, в широком или узком диапазоне, статистическая совокупность распределяется в безынтервальный (дискретный) или интервальный вариационные ряды. Дискретные ряды строятся достаточно просто. А для построения интервального ряда вариацию признака разбивают на группы или классы. Величину классового интервала () рассчитывают по формуле:
![]()
где R – размах, К – число классов, на которые следует разбить вариацию признака.
Величину К можно определить по формуле Стерджеса: К = 1 + 3.32*lgn (или 1 + 1,4* lnn ), n > 100, или по формуле Брукса К = 5*lgn, где n – объем выборки.
В любом более или менее симметричном вариационном ряду заметна одна характерная особенность – накапливание вариант в центральных классах и постепенное убывание их численности по мере удаления от центра ряда. Таким образом, прослеживается широко распространенная в природе закономерность: в статической совокупности большинство вариант оказывается среднего или близкого к нему размера, и чем дальше они отстоят от среднего значения, тем реже встречаются в данной совокупности.
Техника построения вариационных рядов
в исходных данных отыскать минимальную хmin и максимальную xmax варианты.
определить количество классовых интервалов К.
определить величину классового интервала . Точность величины классового интервала должна соответствовать точности, принятой при измерении признака. Если точность измеряемого признака составляет сотые доли единицы, то и классовый интервал берется с точностью до сотых (если точность выражается десятыми долями единицы, то и составит десятые доли единицы).
определить нижнюю границу первого классового интервала по формуле:
хн1 = хmin - /2
определить верхнюю границу первого классового интервала по формуле:
хв1 = хн1 +
Для разграничения классов уменьшить верхнюю границу на величину, равную точности, принятой при измерении признака:
хв1 = хв1 – 0,01 (или 0,1)
определить верхнюю и нижнюю границы второго классового интервала по формуле:
хв2 = хв1 +
хн2 = хн1 +
аналогично определить верхние границы остальных классовых интервалов.
распределить по классовым интервалам все варианты совокупности, т. е. определить частоты каждого класса.
заменить классовые интервалы их центральными (или срединными) значениями по формуле:
хк = (хн1 + хн2)/2
или хк = хн1 /2
В результате интервальный вариационный ряд превращается в безынтервальный ряд. Необходимость такой замены вызывается тем, что обобщающие числовые характеристики (средняя, дисперсия и др.) вычисляются по безынтервальным рядам
Середины (хк) классов приобретают значения отдельных вариант и называются классовыми вариантами в отличие от конкретных вариант, составляющих данную совокупность.
10. построить вспомогательную (расчетную) таблицу, в которой первая графа заполняется классами (в данном случае ранжированными значениями признака), вторая – классовыми вариантами, а третья — служит для учета частот, распределяемых по этим классам.
Пример 1. На основании многолетних клинических наблюдений, проводившихся в Сухумском питомнике обезьян, составлена следующая выборка, включающая 100 анализов на содержание кальция (мг %) в сыворотке крови низших обезьян (павианов гамадрилов), среднее - 11,915:
13,6 |
12,9 |
12,3 |
9,9 |
12,7 |
11,7 |
10,8 |
10,4 |
10,9 |
10,2 |
14,7 |
10,4 |
11,6 |
11,7 |
12,1 |
10,9 |
12,1 |
9,2 |
10,7 |
11,5 |
13,1 |
10,9 |
12 |
11,1 |
13,5 |
11,2 |
13,5 |
10,1 |
14 |
10 |
11,6 |
12,4 |
11,9 |
11,4 |
12,8 |
11,4 |
10,9 |
12,7 |
13,8 |
13,2 |
11,9 |
10,8 |
11 |
12,6 |
10 |
10,3 |
12,7 |
11,7 |
12,1 |
13,8 |
12,2 |
11,9 |
11,6 |
10,6 |
11,1 |
10,7 |
12,3 |
11,5 |
11,2 |
11,5 |
12,7 |
10,5 |
11,2 |
11,9 |
9,7 |
13 |
9,6 |
12,5 |
11,6 |
9 |
11,5 |
12,3 |
12,8 |
12,6 |
12,8 |
12,5 |
12,8 |
11,4 |
12,5 |
12,3 |
14,5 |
12,3 |
12,6 |
11,7 |
12,2 |
12,3 |
11,6 |
12 |
13,5 |
12,5 |
11,6 |
11,9 |
12 |
11,4 |
14,7 |
11,3 |
13,2 |
14,3 |
13,2 |
14,2 |
