3.Наведіть приклади задач, які можна розв’язати з використанням регресійного аналізу.

Регресійний аналіз — розділ математичної статистики, присвячений методам аналізу залежності однієї величини від іншої. На відміну від кореляційного аналізу не з'ясовує чи істотний зв'язок, а займається пошуком моделі цього зв'язку, вираженої у функції регресії.

Регресійний аналіз використовується в тому випадку, якщо відношення між змінними можуть бути виражені кількісно у виді деякої комбінації цих змінних. Отримана комбінація використовується для передбачення значення, що може приймати цільова (залежна) змінна, яка обчислюється на заданому наборі значень вхідних (незалежних) змінних. У найпростішому випадку для цього використовуються стандартні статистичні методи, такі як лінійна регресія. На жаль, більшість реальних моделей не вкладаються в рамки лінійної регресії. Наприклад, розміри продажів чи фондові ціни дуже складні для передбачення, оскільки можуть залежати від комплексу взаємозв'язків множин змінних. Таким чином, необхідні комплексні методи для передбачення майбутніх значень.

Алгоритм:

Нехай у точках x_n незалежної змінної x отримані виміри Y_n. Потрібно знайти залежність середнього значення величини від величини х, тобто , де a — вектор невідомих параметрів . Функцію називають функцією регресії. Звичайно припускають, що є лінійною функцією параметрів а, тобто має вигляд:

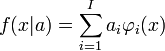(1),

де — задані функції.

У цьому випадку матрицю називається регресійною матрицею.

Для визначення параметрів звичайно використовують метод найменших квадратів, тобто оцінки визначають із умови мінімуму функціонала:

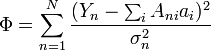
і з мінімуму функціонала: для корельованих вимірів з кореляційною матрицею R.

У якості функцій при невеликих звичайно служать степеневі функції . Часто використовують ортогональні й нормовані поліноми на множині :

.

У цьому випадку легко знайти оцінку :

.

Звідси випливає, що обчислення не залежить від обчислення інших .

Популярне використання в якості сплайнів , які мають дві основні властивості:

1. — поліном заданого степеня;

2. відмінний від нуля в околиці точки .

При пошуку функції регресії у вигляді (1) природно виникає питання про кількість членів I у сумі (1). При малому значенні I не можна досягти гарного опису , а при великому — великі статистичні помилки функції регресії.

4.Як визначається коефіцієнт рангової кореляції Спірмена.

Призначення рангового коефіцієнта кореляції

Метод рангової кореляції Спірмена дозволяє визначити тісноту (силу) і напрям кореляційного зв'язку між двома ознаками або двома профілями (ієрархіями) ознак.

опис методу

Для підрахунку рангової кореляції Спірмена необхідно розташовувати двома рядами значень, які можуть бути проранжовано. Такими рядами значень можуть бути:

1) два ознаки, виміряні в одній і тій же групі випробовуваних;

2) дві індивідуальні ієрархії ознак, виявлені у двох випробовуваних з одного й того ж набору ознак (наприклад, особистісні профілі по 16-факторному опитувальником Р. Б. Кеттелла, ієрархії цінностей за методикою Р. Рокича, послідовності переваг у виборі з декількох альтернатив і ін);

3) дві групові ієрархії ознак;

4) індивідуальна та групова ієрархії ознак.

Спочатку показники ранжуються окремо по кожному з ознак. Як правило, меншому значенню ознаки нараховується менший ранг.

Обмеження коефіцієнта рангової кореляції

1) по кожній змінної повинно бути представлено не менше 5 спостережень;

2) коефіцієнт рангової кореляції Спірмена при великій кількості однакових рангів по одній або обом зіставляєтьсяфразеологічним змінним дає огрублено значення. В ідеалі обидва корелюється ряду повинні представляти собою дві послідовності незбіжних значень.

5. Визначте головні статистичні параметри наведеного нижче варіаційного ряду 10.65;0.08; 5.37;33,70;9.55; 19.51; 1.16; 22,11;42.82; 5.75; 5.27;9.20; 24.85; 34.75;27.66;7.00; 19,59; 49.97; 39.38; 33,61; 44,02; 27,70; 37.09; 7,11.

?

№30