ЗАВДАННЯ

На виконання лабораторної роботи

Побудова і дослідження роботи схем кодеків циклічних кодів.

Мета заняття: поглиблене засвоєння студентами процесів кодування і декодування при застосуванні циклічних кодів.

1. Основні теоретичні положення

Циклічні коди відрізняються високою ефективністю виявлення помилок і порівняно простою реалізацією кодуючих і декодуючих пристроїв у вигляді регістрів з зсувом і зворотними зв’язками.

Циклічний код це код, у якого з приналежної йому комбінації

а_n-1,..., а₁ ,а_0.

шляхом циклічної перестановки отримують також дозволену комбінацію

а_0, а_n-1,..., а_1.

Дозволеними комбінаціями циклічного коду є такі комбінації, які діляться на деякий вихідний (утворюючий) багаточлен Р(х). Комбінація з помилкою (з діапазону помилок, які може виявити даний код) після ділення на Р(х) дасть залишок відмінний від нуля, що свідчить про наявність спотворення у прийнятій комбінації.

При кодуванні багаточлен G(x), що відображає двійковий код повідомлення, яке підлягає передачі, помножують на х^r. Це збільшує довжину кодової комбінації на r розрядів, які потрібні для запису у них перевірочних розрядів.

Добуток G(x) x^r ділять на утворююч ий поліном Р(х), а залишок R(x) від цього ділення складають з G(x) x^r, тобто записують залишок у r молодших розрядів(де після зсуву – перемноження на х^r записані нулі). Отриманий поліном F(x)= G(x) x^r R(x) є комбінацією, що ділиться без залишку на Р(х), тобто він є дозволеною комбінацією даного циклічного коду.

Дійсно, якщо f(x) є частка від ділення G(x) x^r на Р(х), то

G(x) x^r = f(x) P(x) R(x). (43)

Додавши за модулем 2 до правої та лівої частини R(x) отримуємо

G(x) x^r R(x)= f(x) P(x), (44)

Тобто, комбінація F(x) =G(x) x^r R(x) дійсно ділиться на Р(х) без залишку.

До циклічних кодів відносяться коди Боуза-Чоудхурі-Хоквінгема (БЧХ).

Кодуючі та декодуючі пристрої циклічних кодів будують на основі регістрів зсуву з зворотними зв’язками.

Такі регістри здійснюють операцію ділення, яка полягає у послідовному складанні за модулем 2 дільника із старшими розрядами діленого або отриманого на черговому кроці ділення залишку. Регістри складаються з тригерів.

Регістр зсуву з зворотними зв’язками будується у відповідності до обраного утворюючого багаточлена за такими формальними правилами (теоретичною базою побудови таких пристроїв є теорія кінцевих автоматів з пам’яттю):

1. Число каскадів (тригерів) регістра обирають рівним степені ( ) утворюючого багаточлена.

2. Кількість суматорів за модулем 2 береться на одиницю менше числа ненульових членів утворюючого багаточлена.

3. Входи всіх тригерів регістра зліва направо позначають х^і (і=0, 1, 2). Вихід останнього тригера позначається , а вхід першого х⁰.

4. Суматори за модулем 2 встановлюються на вході тих тригерів, для яких у формулі утворюючого багаточлена коефіціент при відповідній степені х^і має ненульове значення. Наприклад, для Р(х) =х³+х+1 (див. рис. 1) суматори встановлюються на входах 1 та 2 (тригерів, що відповідають х⁰ та х).

5. Вихід останнього тригера з’єднується з одним із входів суматорів.

6. Виходи попередніх тригерів з’єднуються з входами наступних через суматори (в залежності від того, встановлені вони між тригерами чи ні) або безпосередньо.

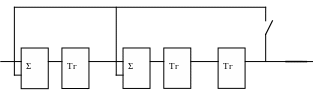Кл1

Кл2; Вих

Х⁰ Х¹ Х²

Рис. 1

2. Завдання на лабораторну роботу.

2.1 Побудова кодеру і дослідження процесу кодування.

Дослідити процес кодування двійкового повідомлення завадостійким циклічним кодом.

Представити свої ініціали у двійковому коді, наприклад, у міжнародному телеграфному коді МТК-2, приписавши у старшому розряді 0 при розташуванні літери на регістрі кирилиці або 1 при розташуванні літери на регістрі чисел та символів, (або у коді Бодо; у коді АSKII, тощо), після чого:

а) визначити відстані Хемінга між кодовими комбінаціями першої та другої, другої та третьої, першої та третьої літер;

б) закодувати кожну із літер завадостійким циклічним кодом, який задається кодоутворюючим поліномом, визначеним викладачем із переліку у Додатку 1.

При цьому необхідно:

• отримати залишки шляхом ділення інформаційних складових на утворюючий поліном;

• сформувати кодові слова, якими повинні бути представлені літери ініціалів при передачі їх в каналі зв’язку;

в) визначити кодову відстань між представленими у циклічному коді літерами ініціалів;

г) у відповідності з кодоутворюючим поліномом розробити функціональну схему кодуючого пристрою;

д) відобразити процес отримання залишку (у вигляді двійкової послідовності) шляхом покрокового заповнення таблиці стану тригерів регістру кодуючого пристрою (для кожної літери);