В2.4. Бином Ньютона
Утверждение. Справедлива формула
(формула бинома Ньютона)
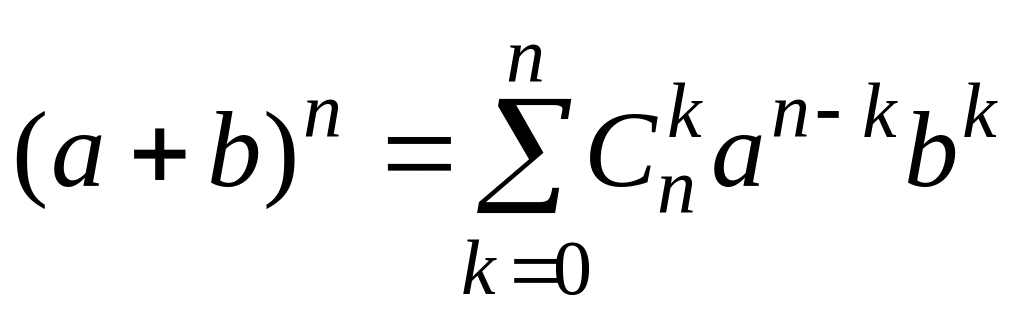 .
.
Доказательство. Воспользуемся
методом математической индукции.
1). База индукции.
( +
+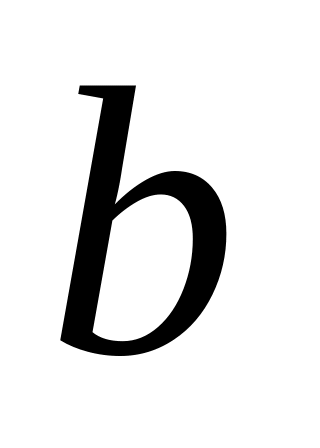 )1=
)1=
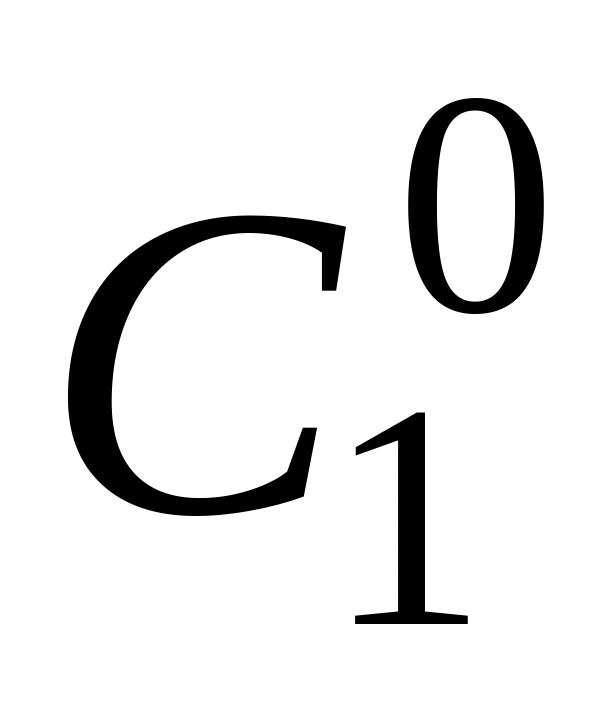
 1
1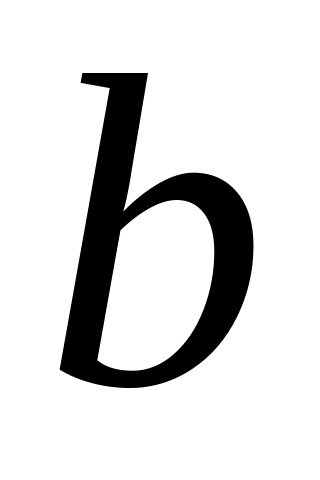 0+
0+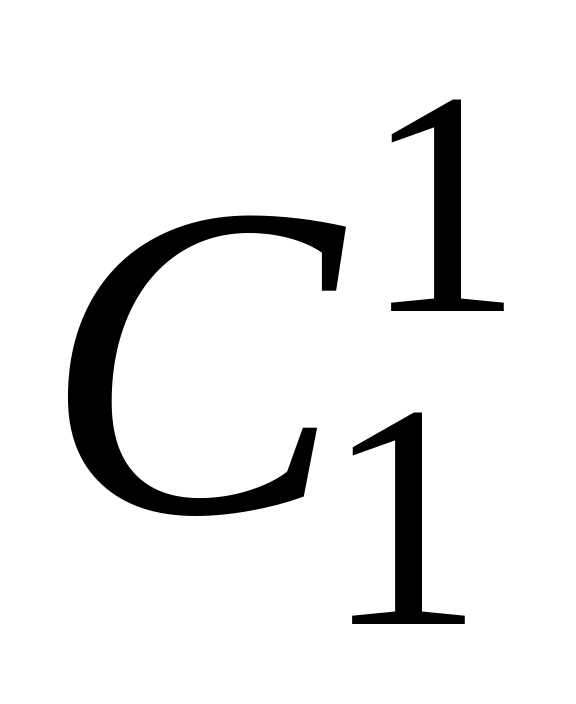 0
1
=
+
;
0
1
=
+
;
(
+
)2=
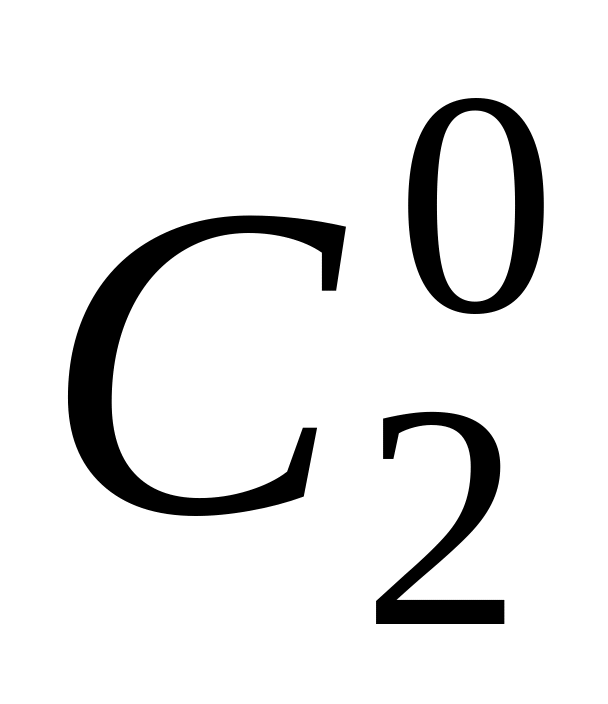 2×
0+
2×
0+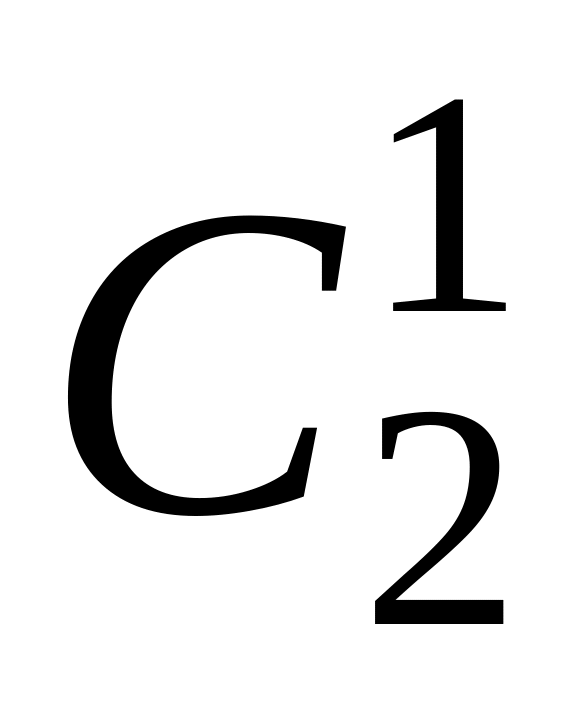 +
+
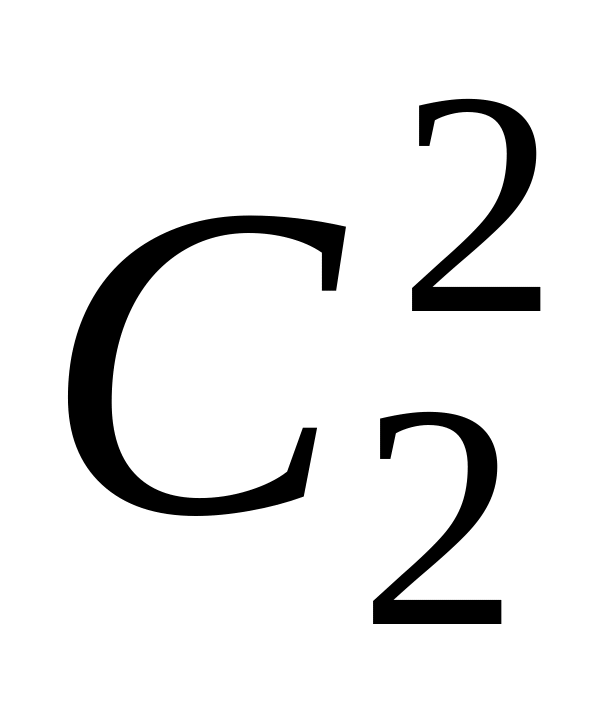 0
2=
2+2
+
2.
0
2=
2+2
+
2.
2). Индуктивное предположение.
Положим, что

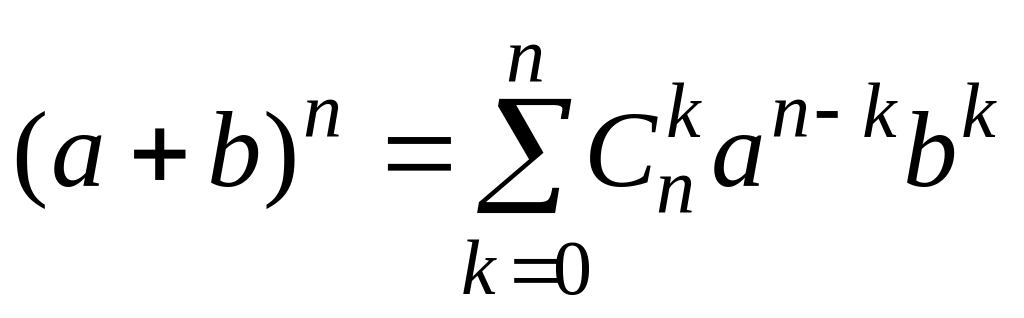 .
.
3). Индуктивный переход.
Доказав истинность следующей формулы,
мы докажем истинность бинома Ньютона.
 .
.
Проведем преобразования и воспользуемся
индуктивным предположением.
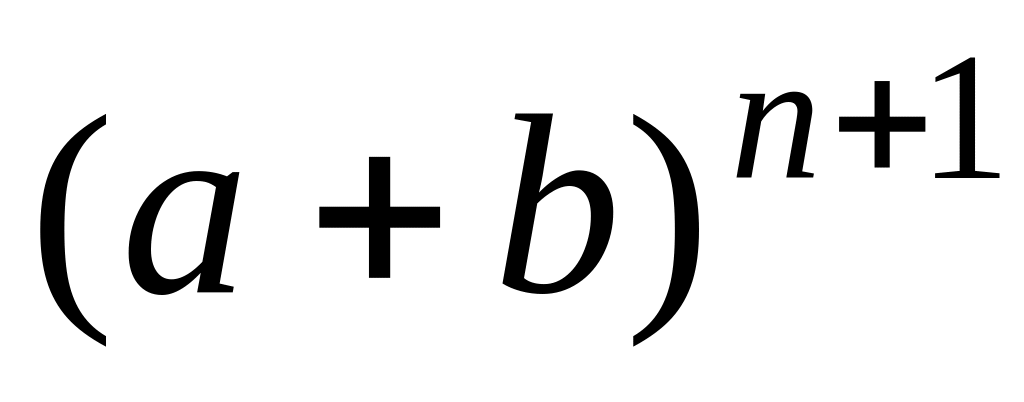 =
=
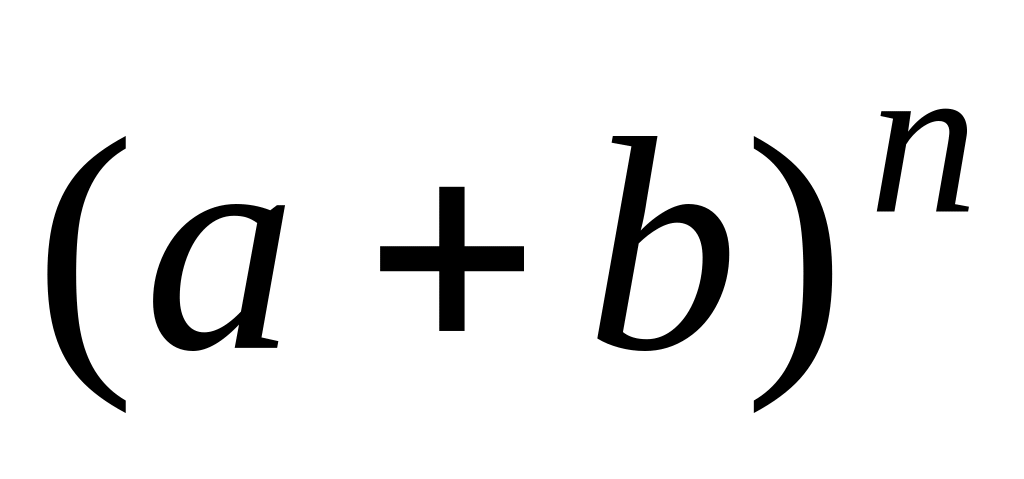 ×
×
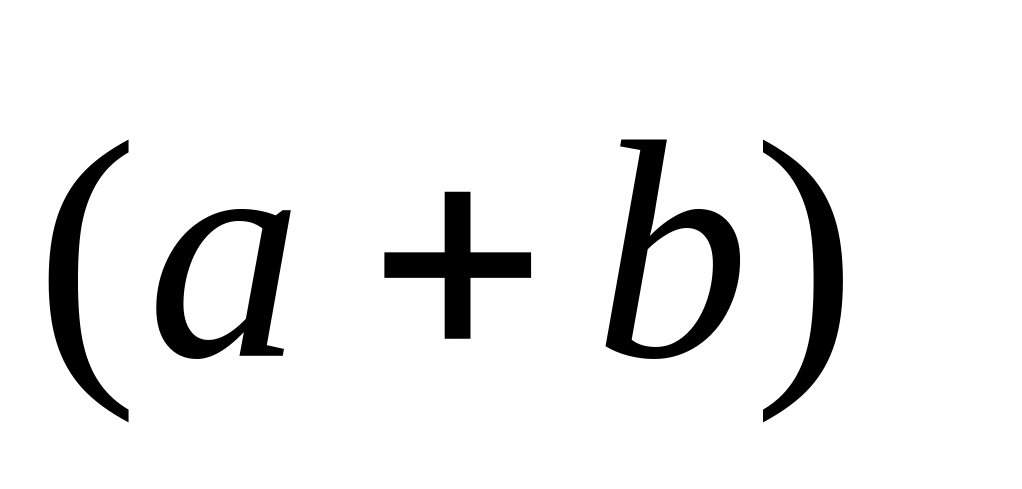 =
=
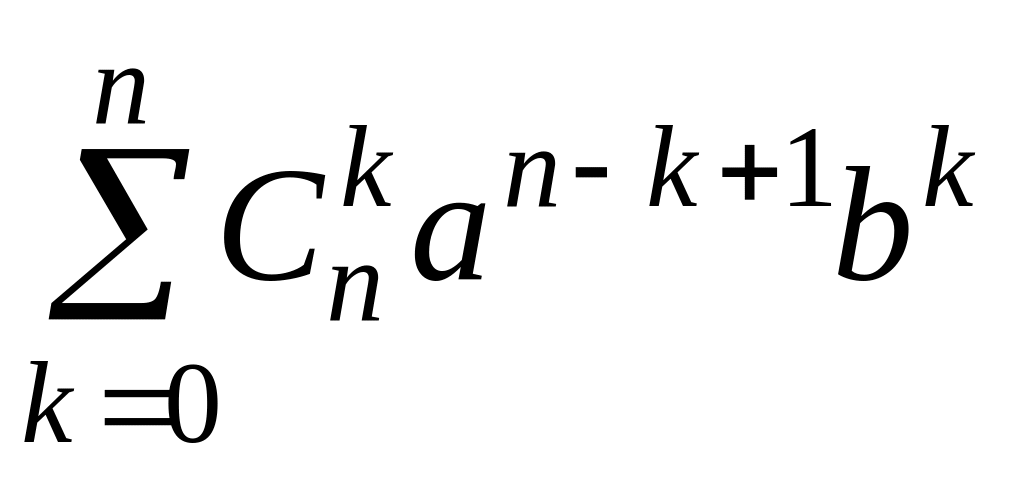 +
+
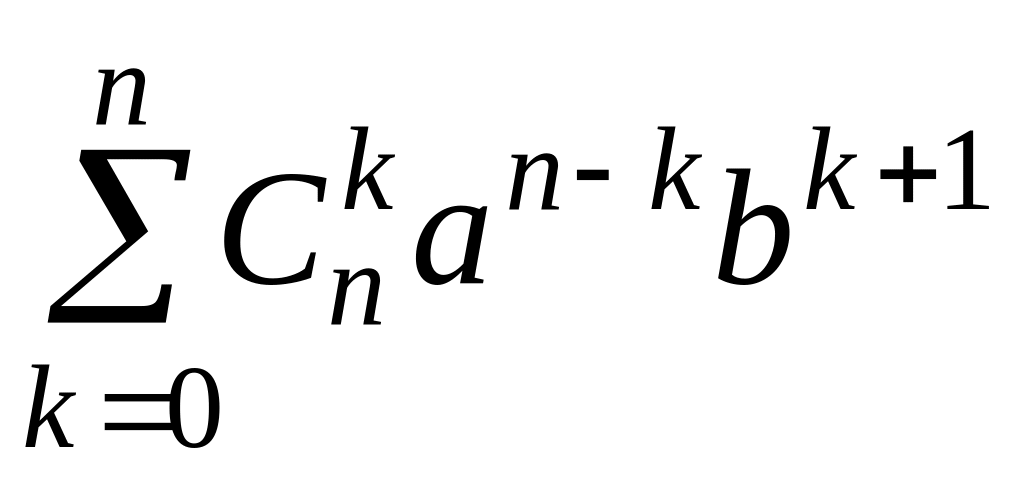 =
=
=
 +
+
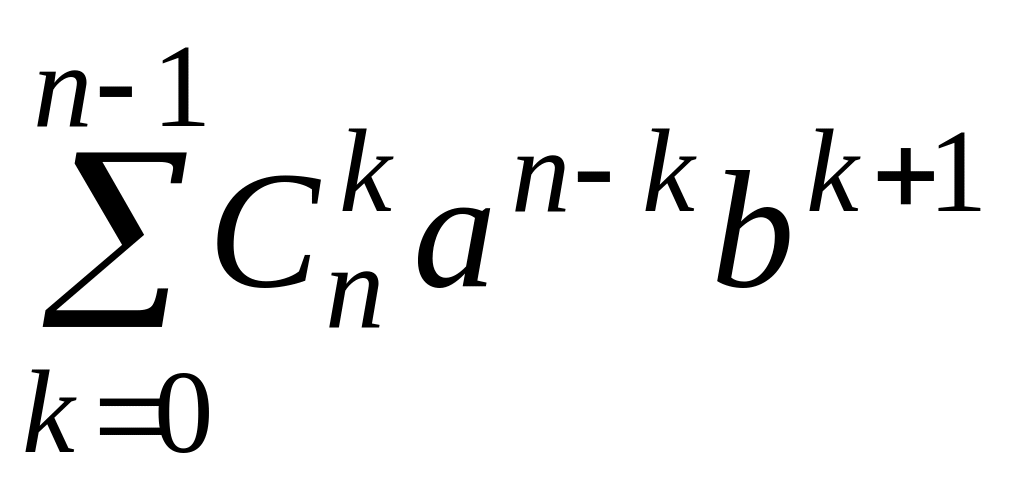 +
+
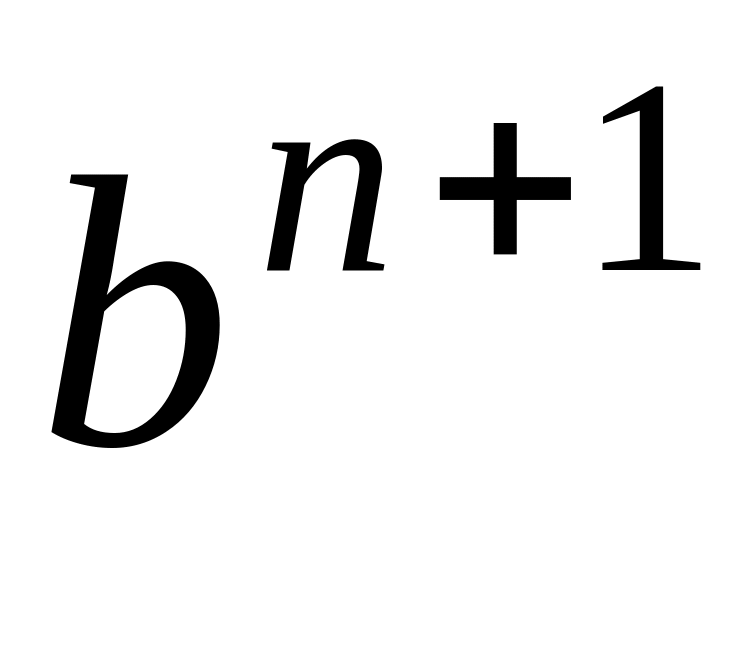 =
n+1
+
=
n+1
+
+
 +
+
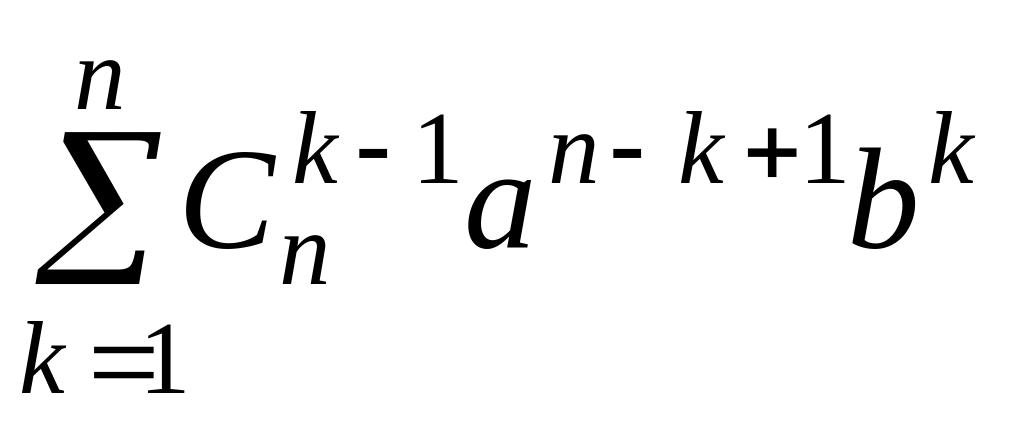 +
n+1.
+
n+1.
Во второй сумме была сделана замена
переменной, чтобы индекс суммирования
менялся не от 0 до n
1, а от 1 до n.
Объединим две суммы и воспользуемся
тем, что
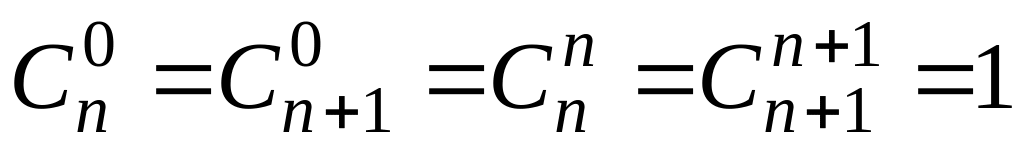 ;
;
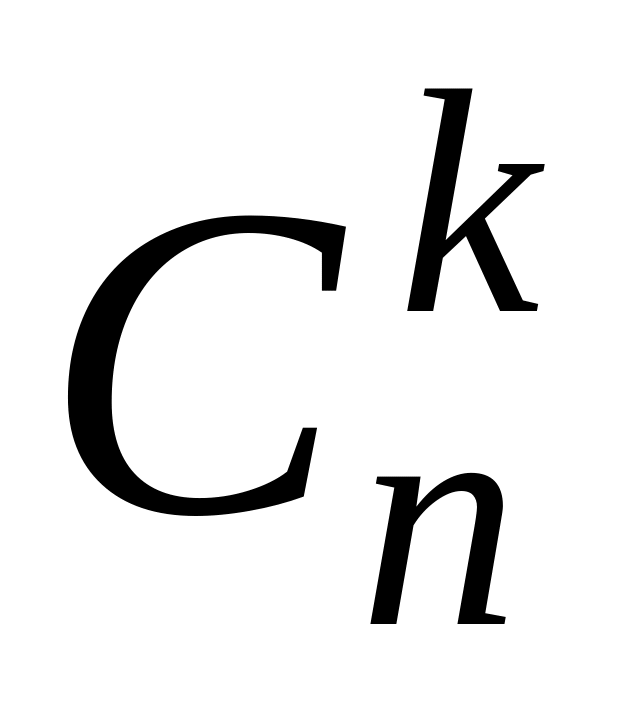 +
+ .
.
Продолжим преобразования
n+1
+
+
+
n+1=
=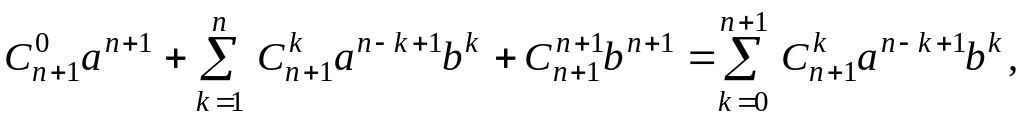
что и требовалось доказать.
Второй способ доказательства формулы
бинома Ньютона.
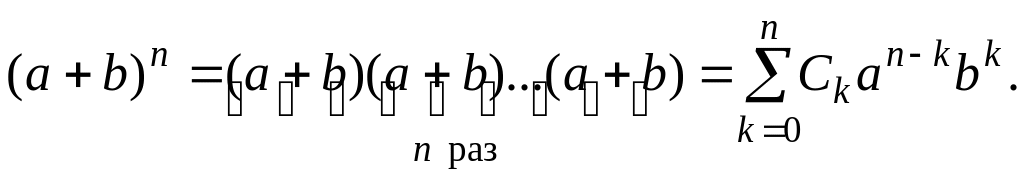 Чтобы получить произведение вида
Чтобы получить произведение вида
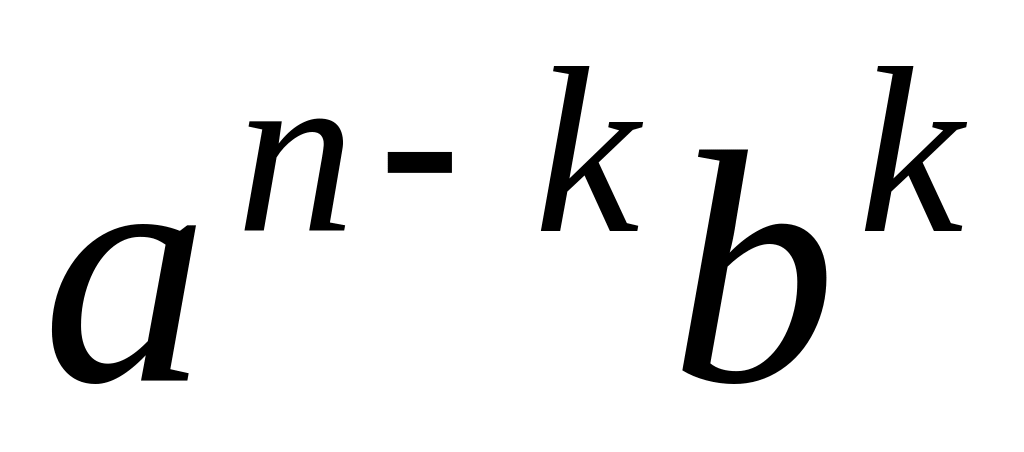 нужно из
нужно из
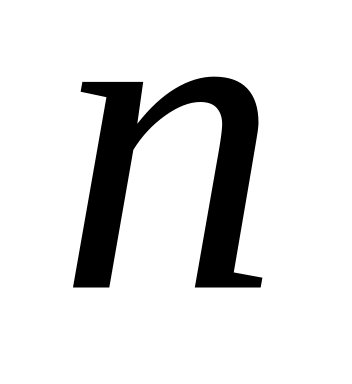 имеющихся скобок отобрать
имеющихся скобок отобрать
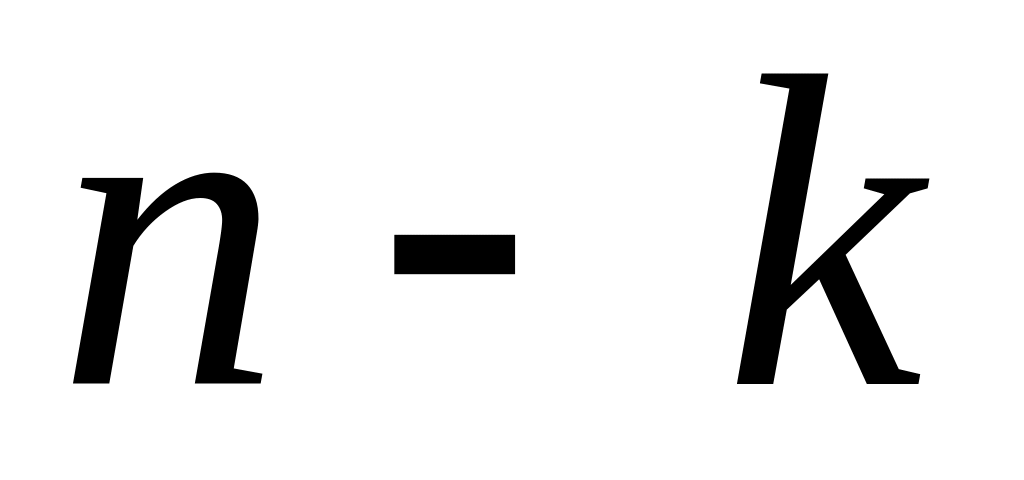 скобок, из которых выбирается сомножитель
а, в оставшихся k
скобках выбрать в качестве сомножителя
b. Но число способов
выбрать
скобок, из которых выбирается сомножитель
а, в оставшихся k
скобках выбрать в качестве сомножителя
b. Но число способов
выбрать
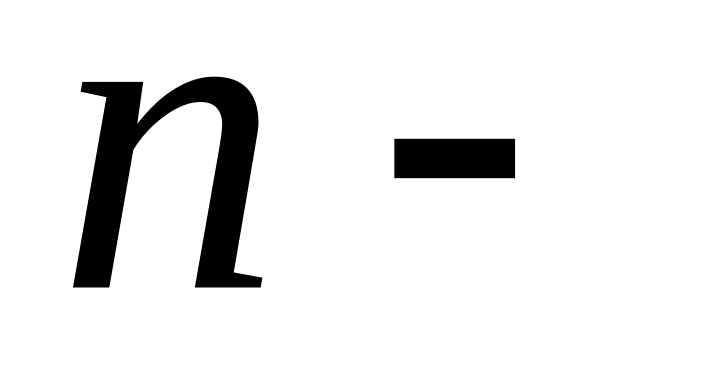 k
скобок из п имеющихся равно
k
скобок из п имеющихся равно
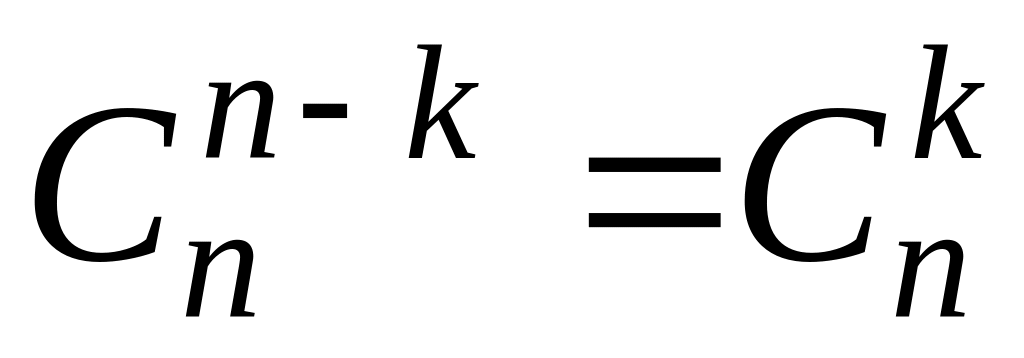 .
Следовательно,
.
Следовательно,
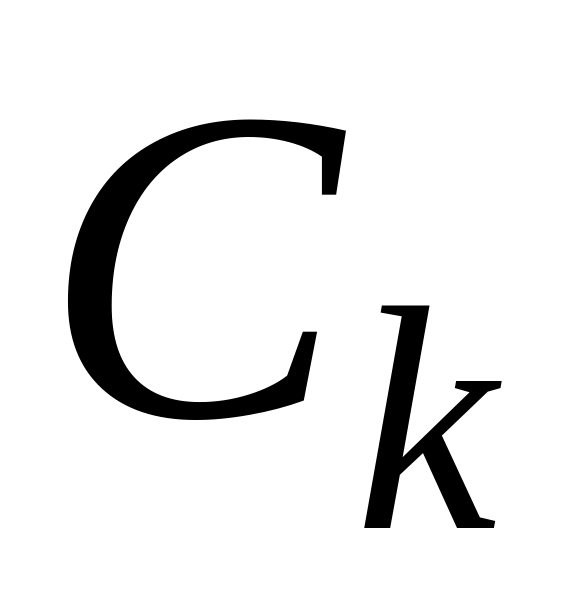 =
,
что и требовалось.
=
,
что и требовалось.
Следствия.
При
=1,
=1:
(1 + 1)n= 2n
=
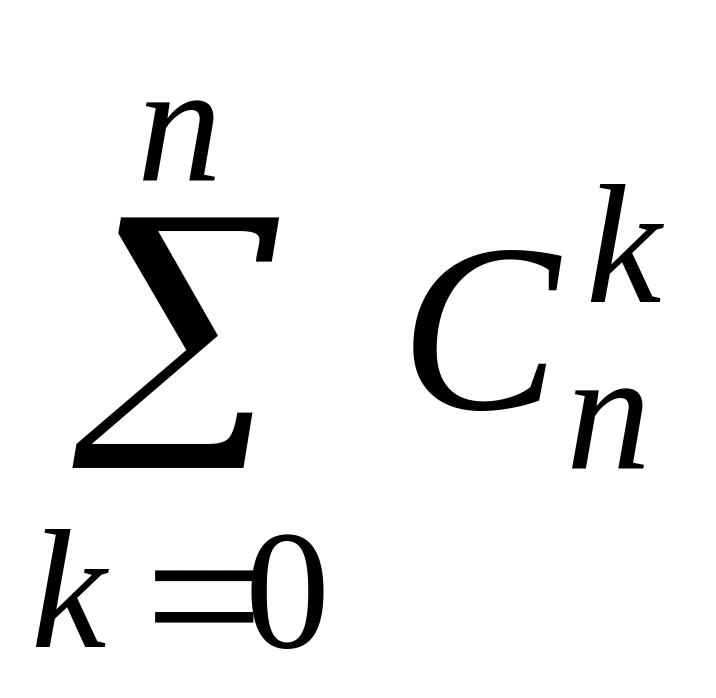 .
.
При
= 1,
=
1: (1
1)n =
0=
(1)k
.
Пример.
24 = 16 =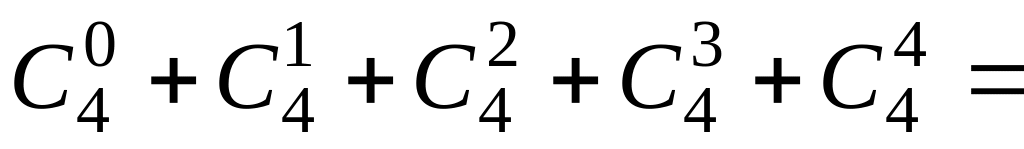 1
+ 4 + 6 + 4 + 1.
1
+ 4 + 6 + 4 + 1.
0 =
 1
4 + 6
4 + 1.
1
4 + 6
4 + 1.


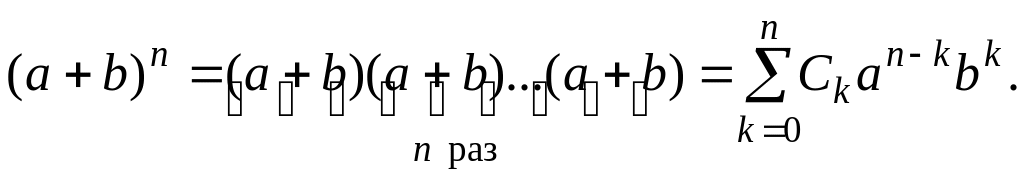 Чтобы получить произведение вида
Чтобы получить произведение вида