
- •2. Плавление и отвердевание кристаллических тел и объяснение этих процессов на основе представлений о дискретном строении вещества. Удельная теплота плавления.
- •Уравнение Теплового Баланса. Первый Закон Термодинамики
- •Первый закон термодинамики
- •Применение первого закона термодинамики к процессам в одноатомных идеальных газах
- •Первый закон Ньютона
- •[Править] Современная формулировка
- •Второй закон Ньютона
- •[Править] Современная формулировка
- •Третий закон Ньютона
- •[Править] Современная формулировка
- •2. Проводники в электростатическом поле. Диэлектрики в электрическом поле. Поляризация диэлектриков. Проводники в электрическом поле.
- •И деальный газ оказывает на стенки сосуда давление 1,01•105 Па. Тепловая скорость движения молекул 500 м/с. Найдите плотность газа.
- •1. Сила упругости. Закон Гука. Силы трения. Силы упругости
- •Закон Гука
- •2. Потенциальность электростатического поля. Потенциал и разность потенциалов.
- •Найти максимальную высоту, на которую поднимется камень, брошенный вертикально вверх со скоростью 20 м/с?
- •1. Импульс. Закон сохранения импульса. Реактивное движение.
- •2. Электроемкость. Конденсаторы. Энергия электрического поля конденсатора.
- •3. Шар массой 1 кг, летящий со скоростью 4 м/с, при ударе сжимает пружину. Найти максимальную энергию сжатия пружины.
- •1. Работа силы. Кинетическая энергия. Потенциальная энергия. Закон сохранения механической энергии. Работа силы (сил) над одной точкой
- •Работа силы (сил) над системой или неточечным телом
- •2. Сила тока. Закон Ома для участка цепи.
- •1. Статика. Момент силы. Условия равновесия твердого тела.
- •2. Сопротивление. Электрические цепи.
- •1. Возникновение атомистической гипотезы строения вещества и ее экспериментальные доказательства. Размеры и масса молекул. Количество вещества. Моль. Постоянная Авогадро.
- •Возрождение и раннее Новое время
- •2. Последовательное и параллельное соединения проводников.
- •[Править] Катушка индуктивности
- •[Править] Электрический конденсатор
- •[Править] Мемристоры
- •3. Через какой промежуток времени с момента старта мотоциклист, двигаясь с постоянным ускорением 5 м/с2 , разовьет скорость 90 км/ч?
- •1. Броуновское движение. Силы взаимодействия молекул. Строение газообразных, жидких и твердых тел. Тепловое движение молекул.
- •Построение классической теории
- •2. Основное уравнение мкт. Давление идеального газа. Связь давления и температуры.
- •3. Резистор сопротивлением r подключен к параллельно соединенным батареям с эдс 1и 2 и внутренними сопротивлениями соответственно r1 и r2. Определить ток, текущий через нагрузку.
- •1. Модель идеального газа. Границы применимости модели. Основное уравнение молекулярно-кинетической теории газа.
- •2. Работа и мощность тока. Электродвижущая сила. Закон Ома для полной цепи.
- •Эдс индукции
- •2. Электрический ток в металлах.
- •3. Напряженность поля в точке а направлена на восток и равна 2 • 105 н/Кл. Какая сила и в каком направлении будет действовать на заряд -3 мкКл?
- •1. Внутренняя энергия. Работа в термодинамике. Количество теплоты. Теплоемкость.
- •Работа в термодинамике
- •2. Зависимость сопротивления от температуры.
- •3. Сила взаимодействия двух одинаковых точечных зарядов, находящихся на расстоянии 0,5 м, равна 3,6 н. Найдите значения этих зарядов.
- •1. Первый закон термодинамики. Изопроцессы. Изотермы Ван-дер-Ваальса. Адиабатный процесс.
- •2. Сверхпроводимость.
- •1. Второй закон термодинамики: статистическое истолкование необратимости процессов в природе. Порядок и хаос.
- •2. . Собственная и примесная проводимости полупроводников, p— n переход. Полупроводниковый диод.
- •1. Тепловые двигатели: двигатель внутреннего сгорания, дизель. Холодильник: устройство и принцип действия. Кпд двигателей. Проблемы энергетики и охраны окружающей среды.
- •2. Транзистор.
- •3. Два шара массами 1 и 2 кг, скользят по гладкой поверхности на запад и север со скоростями 10 и 5 м/с соответственно. Определить направление и модуль импульса системы шаров.
- •2. Электрический ток в жидкостях.
- •1. Влажность воздуха. Кристаллические и аморфные тела. Модели строения твердых тел.
- •2. Электрический ток в вакууме. Электрический ток в газах. Плазма.
3. Шар массой 1 кг, летящий со скоростью 4 м/с, при ударе сжимает пружину. Найти максимальную энергию сжатия пружины.
Максимальная энергия сжатия пружины равна кинетической энергии летящего мяча, которая находится по формуле Е=mv*2/2 (масса умноженная на квадрат скорости и деленная пополам) Значит Е=1х16/2=8 Дж
Билет №9
1. Работа силы. Кинетическая энергия. Потенциальная энергия. Закон сохранения механической энергии. Работа силы (сил) над одной точкой
Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше в этом параграфе будем говорить об одной силе.
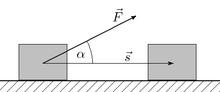
![]()
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
![]()
Здесь точкой обозначено скалярное
произведение[4],
![]() —
вектор
перемещения; подразумевается,
что действующая сила
—
вектор
перемещения; подразумевается,
что действующая сила
![]() постоянна
в течение всего того времени, за которое
вычисляется работа.
постоянна
в течение всего того времени, за которое
вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
![]()
(подразумевается суммирование по кривой,
которая является пределом ломаной,
составленной из последовательных
перемещений
![]() если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
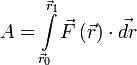 ,
,
где
![]() и
и
![]() —
радиус-векторы
начального и конечного положения тела
соответственно.
—
радиус-векторы
начального и конечного положения тела
соответственно.
Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.
Работа силы (сил) над системой или неточечным телом
Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой.
Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если
![]() —
полная работа, совершённая над частицей,
определяемая как сумма работ совершенных
приложенными к частице силами, то она
выражается как:
—
полная работа, совершённая над частицей,
определяемая как сумма работ совершенных
приложенными к частице силами, то она
выражается как:
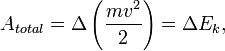
где
![]() называется
кинетической
энергией. Для материальной
точки, кинетическая энергия определяется
как работа силы, ускорившей точку от
нулевой скорости до величины скорости
называется
кинетической
энергией. Для материальной
точки, кинетическая энергия определяется
как работа силы, ускорившей точку от
нулевой скорости до величины скорости
![]() и
выражается как:
и
выражается как:
![]() Для
сложных объектов, состоящих из множества
частиц, кинетическая энергия тела равна
сумме кинетических энергий частиц.
Для
сложных объектов, состоящих из множества
частиц, кинетическая энергия тела равна
сумме кинетических энергий частиц.
Сила
называется потенциальной,
если существует скалярная функция,
известная как потенциальная
энергия и обозначаемая
![]() ,
такая что
,
такая что
![]()
Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
|
|
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
![]()
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
Закон сохранения механической энергииМеханическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может никуда исчезнуть. Для замкнутой системы физических тел, например, справедливо равенство Ek1 + Ep1 = Ek2 + Ep2,где Ek1, Ep1 — кинетическая и потенциальная энергии системы какого-либо взаимодействия, Ek2, Ep2 — соответствующие энергии после.Закон сохранения энергии — это интегральный закон. Это значит, что он складывается из действия дифференциальных законов и является свойством их совокупного действия. Формулировка закона сохранения механической энергии.Полная механическая энергия, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.
