98. Система импликант булевой функции называется полной, если каждая единица бф покрывается импликантой из этой системы.
Определение : Простой (первичной) импликантой булевой функции называется конъюнктивный терм, который сам является импликантой этой функции, но никакая его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного, путем вычеркивания произвольного числа букв
Система S простых импликант булевых функций f называется приведенной, если эта система полна и никакая ее часть не является полной системой импликант функции f. Дизъюнкция всех простых импликант, составляющих S, называется приведенной или тупиковой дизъюнктивной нормальной формой. Всякая минимальная ДНФ является тупиковой ДНФ.
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Тупиковая Дизъюнктивная Нормальная Форма
- представляющая заданную булеву функцию дизъюнктивная нормальная форма (д. н. ф.), к-рую нельзя упростить ни вычеркиванием буквы из нек-рой конъюнкции, ни удалением какой-либо конъюнкции. Минимальная д. н. ф. получается из сокращенной д. н. ф. путем удаления нек-рых конъюнкций; этот неоднозначный, ветвящийся процесс может привести лв тупик
Этапы построения МДНФ:
ФУНКЦИЯ – СДНФ – ТДНФ - МДНФ
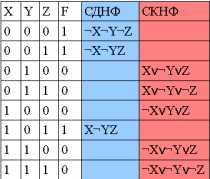
99. Построение СДНФ
Нормальная форма логической формулы - это формула, которая не содержит знаков импликации, эквиваленции и отрицания неэлементарных формул.
Существует
два вида нормальных форм: конъюнктивная
нормальная форма, т. е. конъюнкция
нескольких дизъюнкций (КНФ) и дизъюнктивная
нормальная форма, т. е. дизъюнкция
нескольких конъюнкций (ДНФ).
КНФ: 
ДНФ: 
Совершеная дизъюнктивная нормальная форма (СДНФ)> – такая дизъюнкция конъюнкций, в которой:
Различны все члены конъюнкции ("множители");
Различны все члены каждой дизъюнкции ("слагаемые");
В каждой дизъюнкции нет одновременно переменной и ее отрицания;
Каждая дизъюнкция содержит все переменные, входящие в данную формулу или их отрицания.
СДНФ:
Приведение формулы к сднф с помощью равносильных преобразований:
Привести формулу к нормальному виду (т.е. избавиться от импликации, эквиваленции и отрицания неэлементарных формул).
Из всех одинаковых членов дизъюнкции ("слагаемых") оставить только один.
Если в каком-то члене дизъюнкции ("слагаемом") не хватает переменной Xi, то "домножаем" его с на (Xi?¬Xi), т.е. на 1 .
Раскрыть скобки и из всех одинаковых членов дизъюнкции ("слагаемых") оставить только один.
Для построения СДНФ по таблице истинности необходимо:>
Выбрать из таблицы истинности те строки, в которых значение формулы - "Истина".
Для каждой выбранной строки составить конъюнкцию переменных или их отрицаний так, чтобы эта конъюнкция была истинной (для этого переменные, которые в соответствующей строке имеют значение "Ложь" нужно взять с отрицанием, а переменные, имеющие значение "Истина" - без отрицания).
Составить дизъюнкцию полученных конъюнкций.
