1. Нормальним називають розподіл імовірностей безперервної випадкової величини, яка має щільність:
_ 1 1 (&#)2
/(х,х,<т) = -^е 2 ст2
де х - математичне очікування або середня величина. Як видно, нормальний розподіл визначається двома параметрами: х і ° . Щоб задати нормальний розподіл, досить знати математичне очікування, або середню і середнє квадратичне відхилення. Ці дві величини визначають центр групування і форму
кривої на графіку. Графік функції ї(хх,ст) називається нормальною кривою (крива Гаусса) з параметрами х і ст (рис. 12).
Крива нормального розподілу має точки перегину при X ± 1. Якщо уявити графічно, то між X=+l і 1=-1 знаходиться 0,683 частини всієї площі кривої (тобто 68,3%). У границях X=+2 і X- 2. знаходяться 0,954 площі (95,4 %), а між X=+3 і X= - 3 - 0,997 частини всієї площі розподілу (99,7%). На рис. 13 проілюстрований характер нормального розподілу з одно-, дво- і трисигмовою границями.
При нормальному розподілі середня арифметична, мода і медіана будуть рівними між собою. Форма нормальної кривої має вид одновершинної симетричної кривої, вітки якої асимптотично наближаються до осі абсцис. Найбільша ордината кривої відповідає х = 0 . У цій точці на осі абсцис розміщується чисельне значення ознак, яке дорівнює середній арифметичній, моді і медіані. По обидві сторони від вершини кривої її вітки спадають, змінюючи в певних точках форму випуклості на увігнутість. Ці точки симетричні і відповідають значенням х = ±1, тобто величинам ознаки, відхилення яких від середньої чисельно дорівнює середньому квадратичному відхиленню. Ордината, що відповідає середній арифметичній, ділить всю площу між кривою і віссю абсцис пополам. Отже, ймовірності появи значень досліджуваної ознаки більших і менших середньої
арифметичної будуть рівні 0,50, тобто х,(~^х) = 0,50 У
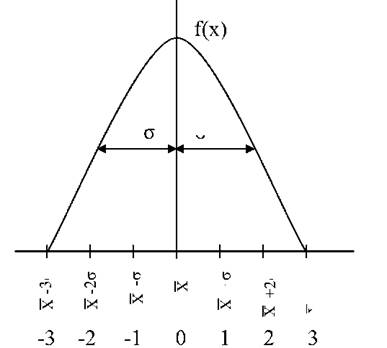
Рис.12. Крива нормального розподілу (крива Гауса)
2. Після визначення мети і задачі дослідження, а також встановлення
доцільності опрацювання матеріалів експериментальних досліджень
біологічного або екологічного об’єкту методами кореляційного аналізу
проводиться визначення номінальних ознак, що обрані для порівняння,
шляхом вимірювання, зважування, встановлення кількості, визначення
кольору та інше. Одна з аналізованих ознак приймається як незалежна
(аргумент) (х), друга − як сполучена ознака (у) (функція). Звичайно як
незалежну обирають ту ознаку або той елемент, який більш доступний для
спостереження.
Розміщення залежної ознаки відносно незалежної на осі координат може
бути прямолінійним або криволінійним.
Кореляційний зв’язок характеризується коефіцієнтом кореляції (r), який
має значення в межах від 0 до +1 і від 0 до −1. При значенні r від 0 до +1
маємо справу з прямою кореляційною залежністю, коли це значення від 0 до
−1 − залежність зворотня. Чим ближче значення коефіцієнта кореляції наближається до 1, тим
тісніший (більш щільний) зв’язок між ознаками, що досліджуються.
Коли r = ±1, маємо справу з функціональним прямолінійним характером
зв’язку.
Коли r наближається до 0, то вірогідність наявності прямолінійного
зв’язку між ознаками дуже мала, однак тіснота криволінійного зв’язку може
бути досить високою.
При наявності кореляції дослідник має справу не з прирощенням
(збільшенням або зменшенням) функції, а із взаємосполученою варіацією
ознак. Варіації певної кількості ознак (у), яка відповідає відповідному
значенню аргументу (х), від середнього ії значення характеризується
показником, який має назву коваріації (Cov). Коефіцієнт кореляції, який визначається для відповідної виборки варіант,
так саме, як і окремі варіанти, що досліджуються, є величина випадкова.
Тому виникає необхідність також визначати ступінь його наближення до
показника генеральної сукупності значень r. Цей показник позначається
літерою (ρ). Для вирішення наведеного завдання також застосовується
нульова гіпотеза. Вона полягає в припущенні, що
ρ = 0, тобто, що між випадковими величинами Х і Y кореляція відсутня.