Лабораторная работа №1(1)

Санкт-Петербургский государственный электротехнический университет

КАФЕДРА ФИЗИКИ ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ N1 по дисциплине "Ф И З И К А" «ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ В ПРОВОДЯЩЕЙ СРЕДЕ» Преподаватель: студент гр. 0341 Юбрин А.Н. Санкт-Петербург 2001

Протокол лабораторной работы:

Номер электрода	1	2
Потенциал В

№	1	2	3	4	5	6	7	8	9	10
, В

Цель работы: исследование конфигурации электростатического поля; построение эквипотенциалей и линий напряженности для заданной формы электродов; приобретение, навыков в приме­нении теоремы Гаусса на примере определения электроемкости системы по экспериментально найденному распределении поля.

Приборы и принадлежности: пантограф с зондом, измерительная схема, лист, чистой бумаги.

Общие сведения

Электростатическое поле определено, если в каждой точке пространства известны величина и направление вектора напряженности Е или значение потенциала  этого поля. В первом случае мы имеем дело с векторным представлением поля, во втором - со скалярным. Между этими представлениями существует связь, выражается соотношением:

В диэлектриках электростатическое поле характеризуется вектором электрического смещения (электрической индукцией) D=_ , который удовлетворяет теореме Гаусса: , где Q— суммарный сторонний заряд, заключенный в объеме, ограниченном поверхностью S. Для однородного диэлектрика

Электрическое поле потенциально, т. е. работа электрических сил по перемещению заряда не зависит от формы траек­тории; работа по замкнутому пути равна нулю. Математически это соответствует тому, что циркуляция вектора напряженности электростатического поля также равна нулю:

Соотношения и дают исчерпывающее описание свойств электростатического поля. В данной работе рассматриваются две типичные задачи электростатики: определение и Е поля заданного распределения зарядов и вычисления емкости системы проводников.

Во многих случаях прямой расчет электростатического по­ля заменяют его моделированием. Наиболее удобной моделыо является электрическое поле в проводящей среде.

Если электроды, к которым приложена разность потенциалов, помещены в проводящую среду то в межэлектродном пространстве возникает электрический ток, плотность которого j связана с напряженностью Е электрического поля, установившегося в среде, законом Ома:

где  - удельная проводимость среды. Таким образом, линия тока (траектории движения носителей тока в проводящей среде) совпадают с линиями напряженности электрического поля. В отсутствие сторонних сил линии тока будут перпендикулярны поверхностям равного потенциала, следовательно, соотношение справедливо и для электрического поля в проводящей среде.

Продолжая аналогию, можно для электрического поля в проводящей среде найти соотношение, подобное теореме Гаусса . Если не рассматривать перенос заряда сторонними сила­ми, то из очевидного выражения:

где I -ток, текущий от электрода; S - замкнутая поверхность, охватывающая электрод, придем к соотношению: , подобному . Потенциальный характер электрического поля в проводящей среде иллюстрируется соотношением: , которое легко доказать, вычисляя, например, циркуляцию век­тора j по замкнутому контуру L , расположенному на эквипотенциальной поверхности. Учитывая , получим подобное выражение:

На основании подобия свойств векторов Е и Е_J можно сделать вывод о возможности моделирования электростатическо­го поля электрическим полем в проводящей среде, если соблюдается подобие формы и расположения электродов в пространстве. Масштабные коэффициенты проводящей модели вычисляются из сопоставления тока I и заряда Q , а также удельной про­водимости  и абсолютной диэлектрической проницаемости _модели и электростатического аналога с учетом их размеров.

Электрическое поле проводящей модели определяют, изме­ряя распределение потенциалов в ней, после чего, используя , рассчитывают поле вектора напряженности.

Электроемкость систему электродов можно определять пря­мым измерением сопротивления проводящей Среды между электродами. Можно показать, что

R - сопротивление проводящей среды. Можно также вычислить емкость электродов использованием теоремы Гаусса, учитывая, что С=Q/U, где U - напряжение равное разности потен­циалов между электродами модели, получаем для определения ем­кости 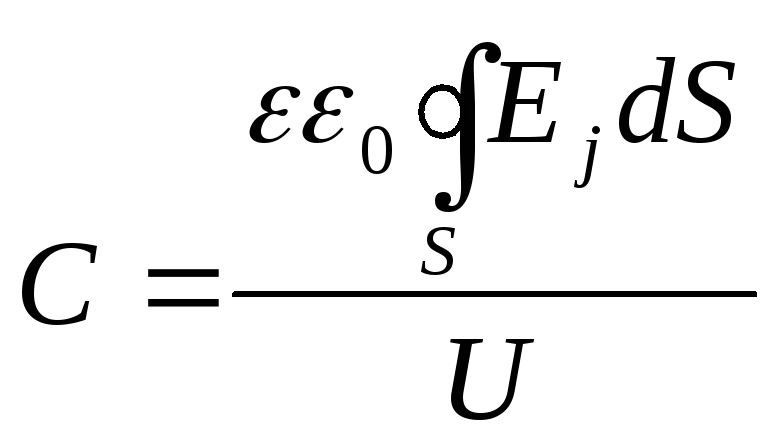, здесь поток вектора Е_J вычисляется по поверхности, охватывающей электрод моделируемой системы  относительная диэлектрическая проницаемость моделируемого диэлектрика. Соотно­шение 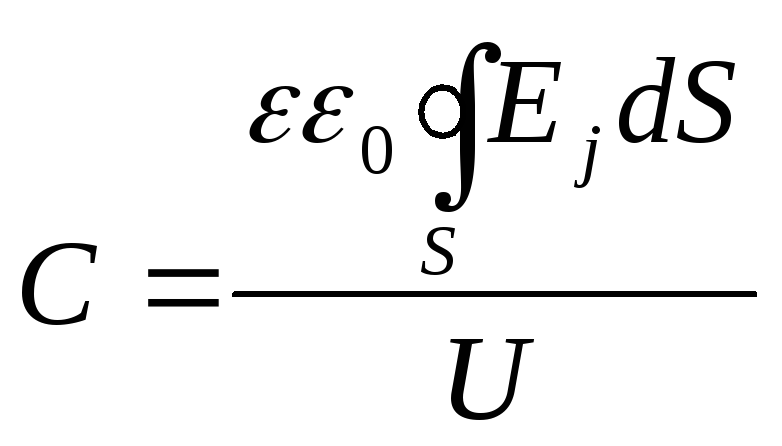удобно тем, что в качестве поверхности S берется определенная по модели эквипотенциальная поверхность.

Методика измерений. В настоящей работе моделируется плоское поле, т. е. такое, потенциал и напряженность кото­рого зависят от двух координат. Плоским является, например, поле двухпроводной линии или же поле, образованное заряженными плоскостью и проводником. Для описания таких полей до­статочно найти распределение в плоскости, перпендикулярной к электродам, тогда полная картина поля образуется смещением полученного сечения вдоль оси, перпендикулярной к этому сече­нию.

В экспериментальной установке воспроизводится сечение системы электродов формирующих один из возможных вариантов плоского поля. В качестве проводящей среды используется про­водящая бумага. Электрическая схема измерительной установки приведена на рис.1.

Схема представляет собой мост постоянного тока, одно плечо которого образовано сопротивлениями участков ab и bc потенциометра R1 между его концевыми и подвижным контакта­ми; другое плечо - сопротивлениями участков проводящей бумаги (1) между зондом (2) и электродами. В диагональ моста включен микроамперметр PA1. Ток в диагонали моста равен нулю, когда падение напряжения на участке bc резистрора R1 равно разности потенциалов между зондом и нижним по схеме электро­дом. Потенциал одного электрода принимается равным нулю. Перемещая зонд по листу проводящей бумаги, можно исследовать распределение потенциала на поверхности листа. С помощью пан­тографа координату зонда переносятся на чистый лист бумаги, эакрепленный под вторым плечом пантографа Если отмечать точ­ки, соответствующие одному и тому же падению напряжения на участке bc резистора R1, а затем менять его с заданным шагом  , то в результате получится карта эквипотенциалей с шагом . Примерный вид карты поля около одного из электродов моделируемой системы приведен на рис.2.

Для построения линий напряженности (силовых линий) исполь­зуется следующий прием. В начале проводят линию CO` (рис.2), соединяющую электроды так, чтобы она совпадала с осью симметрии поля. От точки О вдоль контура

электрода откладываот отрезок O-O1, равный кратчайшему рас стоянию 01 от точки O до эквипотенциали , и получают точку O, затем от точки О1 откладывают отрезок О1 - О2 ,равный кратчайшему расстоянию O₁1₁, от точки О1 до эквипотенциали , получают точку O2 и т.д. Последней точкой на контуре электрода будет та, от которой откладывается отрезок, накрывающий точку O1 , диаметрально противоположную точке O. Аналогичное построение проводят от точки 0 в другую сторону. Разделив указанный образом ближайшую к электроду эквипотенциаль через полученные точки 1₁1₂ ... проводят перпендику­лярные к ней отрезка до пересечения со следующей эквипотенциалью карты поля, полученные точки следует соединить плавными линиями, соблюдая их ортогональность эквипотенциальным линиям в точках пересечения.

Для вычисления емкости, приходящейся на единицу длины рассматриваемых электродов, необходимо с помощью формулы рассчитать поток вектора напряженности через поверх­ность, охватывающую единицу длины электрода. Для этого следу­ет представить, что ближайшая к электроду замкнутая эквипотенциаль является цилиндром, образующая которого перпендику­лярна плоскости листа. Полагая напряженность поля в пределах каждого из отрезков l_iпримерно одинаковой, можно вычислить _i поток вектора E_i, через i -й элемент поверхно­сти цилиндра: , где h. - высота цилиндра, l_i -длина отрезка эквипотенциали, измеряемая по карте поля. Еi определяется по формуле - , r_i - расстояние между соответствующими отрезками электрода и ближайшей к нему эквипотенциалью; (  -  ) - разность потенциалов между электродом и ближайшей к нему эквипотенциалью. Заряд, заключенный внутри замкнутой поверхности цилинд­ра, вычисляется по теореме Гаусса суммированием потоков через все элементы поверхности цилиндра:

Последнее соотношение используется для нахождения емко­сти единицы длины (погонной емкости) моделируемой системы:

Рисунок 1. Схема измерительной установки.

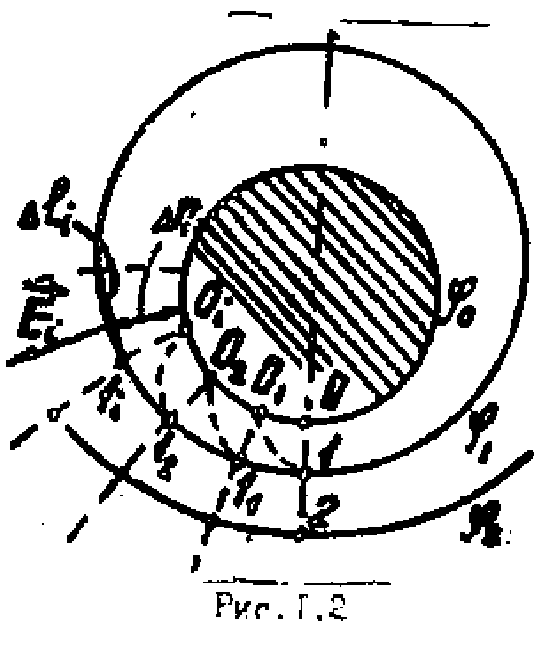
Рисунок 2. Вид карты поля.

Расчет лабораторной работы:

1. Векторы напряженности

E=(₀-₁)/r_i

r_i – определяется из карты поля, как расстояние между средними точками отрезков на поверхности электрода и на ближайшей эквипотенциали.

(₀-₁) – разность потенциалов между электродом и эквипотенциалью.

(₀-₁)=8,7-7=1,7В

№	1	2	3	4	5	6	7	8	9	10	11	12
ri,м.10-3	7	8	9	11	22	34	16	8	6	5	5	6
E, В/м.103	0,24	0,21	0,19	0,15	0,08	0,05	0,11	0,21	0,28	0,34	0,34	0,28

2. 

№	1	2	3	4	5	6	7	8	9	10	11	12
li,м.10-3	10	11	15	25	57	33	16	8	6	7	10	12
li/ri, .10-3	1,43	1,37	0,67	2,27	2,59	0,97	1	1	1	1,4	2	2

=18,79

С_k=[1^.8,85^.10^-12(8,7-7)/220] 18,79=1,28^.10^-12 Ф/м

3. Аналитическое выражение для емкости моделируемой системы.

В настоящей работе моделируется плоское поле (потенциал и напряженность такого поля зависят от двух координат).

Плоским является, например, поле двух проводной линии.

Пусть r радиус проводов, а l – расстояние между их центрами. Поле внутри металлических проводов E=0. Поле между проводами E=E₊+E_-=

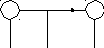+q E₊ E_- -q

x l-x

Разность потенциалов между проводами:

₁-₂=

=>

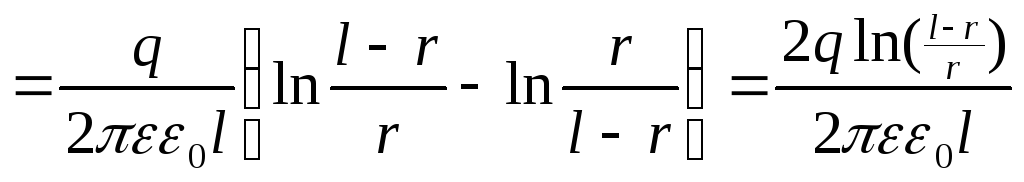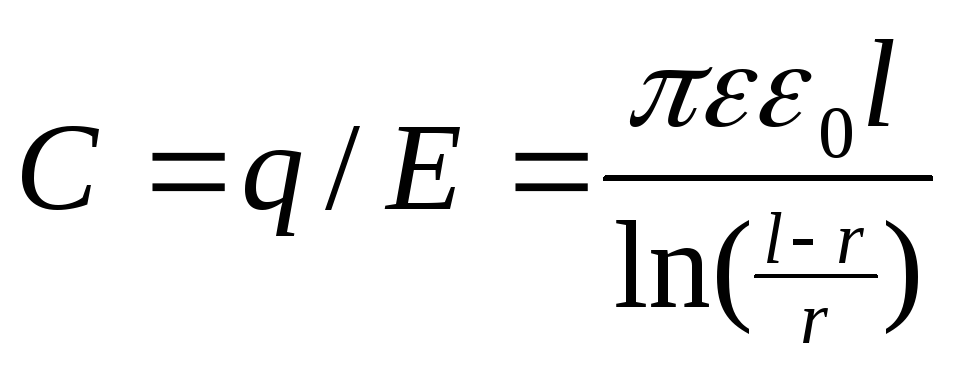
l=130^.10^-3м ; r=15^.10^-3м

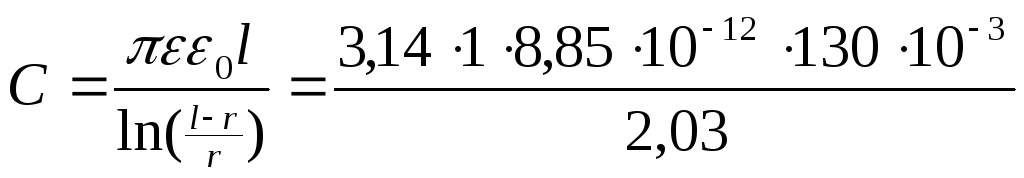=1,79^.10^-12 Ф/м

4. Плотность энергии электрического поля в пределах каждого из отрезков.

=_(E²/2)

№	1	2	3	4	5	6	7	8	9	10	11	12
E, В/м.103	0,24	0,21	0,19	0,15	0,08	0,05	0,11	0,21	0,28	0,34	0,34	0,28
, .10-8	25,49	19,51	15,97	9,96	2,83	1,11	5,35	19,51	34,69	51,15	51,15	34,69