Лабораторная работа №51

Санкт-Петербургский государственный электротехнический университет

КАФЕДРА ФИЗИКИ ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ N5 по дисциплине "Ф И З И К А" «Определение скорости распространения звука в воздухе». Преподаватель: студент гр. 0341 Юбрин А.Н. Санкт-Петербург 2000

№	L1		L2		L3
1	192	190	360	361	536	536
2	189	191	359	360	535	539
3	187	192	360	362	534	532
4	190	191	358	360	537	536
5	189	190	361	359	536	537

Для L2 A0=7 v0=1000 Гц t=27	Ay	Vy
	5,6	1010
	4	1020
	3,5	1030
	5,5	990
	4	980
	3	970

1. Цель работы: определение скорости распространения звуковых колебаний в воздухе при данной температуре методом стоячих волн.

2. Приборы и принадлежности: установка акустического резонанса, электронный осциллограф, звуковой генератор.

Исследуемые закономерности

Звуковые колебания в газе представляют собой периодическое чередование сжатий и разрежений, распространяющихся со скоростью, зависящей от свойств воздуха. Газы, в отличие от твёрдых тел, не обладают деформацией сдвига, поэтому в них возникают только продольные волны. Продольные волны обусловлены объёмной деформацией.

Если сжатие происходит быстро, то выделяющееся при этом тепло не успевает распространиться в соседние слои. Сжатие без отвода тепла называется адиабатическим; в этом случае скорость распространения звука рассчитывают по формуле: и = (p/)^1/2 (1).

где  = Ср/Сv ~ отношение теплоёмкостей газа при изобарическом и изохорическом процессах (для воздуха  = 1.4);

p и  - соответственно, средние значения давления и плотности во всем объёме.

Соотношение (1) может быть преобразовано с учетом уравнения состояния идеального газа (V = (т/)RТ), u = (RT/)¹/²,

где R - газовая постоянная; Т - температура;  - молярная масса газа (для воздуха = 29 10^-3 кг/моль)

Удобным методом измерения скорости звуковых волн, является метод, основанный на измерении длины волны , стоячих звуковых волн. Если измерена , и известна частота v возбуждаемых звуковых волн, то u =v.

Стоячие звуковые волны возникают при интерференции падающей и отраженной волн. Точки, в которых амплитуда колебаний максимальна, называются пучностями стоячей волны. Точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.

Явление резонанса наблюдается в том случае, если длина резонатора L_n в котором устанавливается стоячая волна, равна целому числу полуволн

L_n = n/2, где n= 1, 2, 3,...

Явление резонанса резко выражено в том случае, если затухание мало. В данном случае затухание обусловлено неполным отражением волн и потерями на излучение из резонатора в окружающую среду, потому оно невелико и можно считать, что период колебаний

Характеристикой убыли энергии при затухании служит добротность системы

Q=W(t)/(W(t) - W(t + T)).

Знаменатель представляет убыль энергии за период, отсчитываемый от момента времени t. Добротность может быть определена также формулой Q= N_e,

где Nе - число колебаний за время, в течении которого амплитуда колебаний уменьшается в е раз.

Небольшая расстройка частоты относительно резонансной позволяет наблюдать изменение позволяет наблюдать изменение амплитуды колебаний в соответствии с амплитудно-частотной характеристикой резонатора: Av=Ao/(l+((v-v₀)/v₀)² )^1/2 , где A₀ и v₀ - амплитуда и частота при резонансе, v₀ - расстойка частоты от резонанса, при которой А = 2^-l/2Ao.

1. Вычисление средних значений и доверительных погрешностей длины резонатора для каждого из трех резонансов.

Расчет среднего L_1, L_2, L₃:

Расчет среднеквадратических отклонений:

;;

;;

;;

Расчет случайной погрешности:

По Стьюденту:

t_P,N=2.3

;

;

;

Расчет полной погрешности

1,6

1,34

1,86

Результат в округленной форме:

с вероятностью 95%

с вероятностью 95%

с вероятностью 95%

2. Вычисление средних значений и доверительных погрешностей длины волны для каждого из трех резонансов.

Значения 
L1	384	380	378	382	374	364	380	382	378	380
L2	360	361	359	360	360	362	358	360	361	359
L3	357,33	357,33	356,67	359,33	356	354,67	358	357,33	357,33	358

Расчет среднего _1, _2, ₃:

Расчет среднеквадратических отклонений:

;;

;;

;;

Расчет случайной погрешности:

По Стьюденту:

t_P,N=2.3

;

;

;

Расчет полной погрешности

4,64

1,34

1,4

Результат в округленной форме:

с вероятностью 95%

с вероятностью 95%

с вероятностью 95%

3. Вычисление скорости звука по экспериментально полученным значениям

Среднее арифметическое 

₁₂₃)/3=365,13мм

₁₂₃)/3=2,43мм

u=365,13*1000=3,6513*10⁵мм/с=365,13м/с

u=2.43м/с

u=м/с

с вероятностью 95%

4. Вычисление скорости звука по формуле:

u = (RT/)¹/²=347м/с

5. Резонансная кривая.

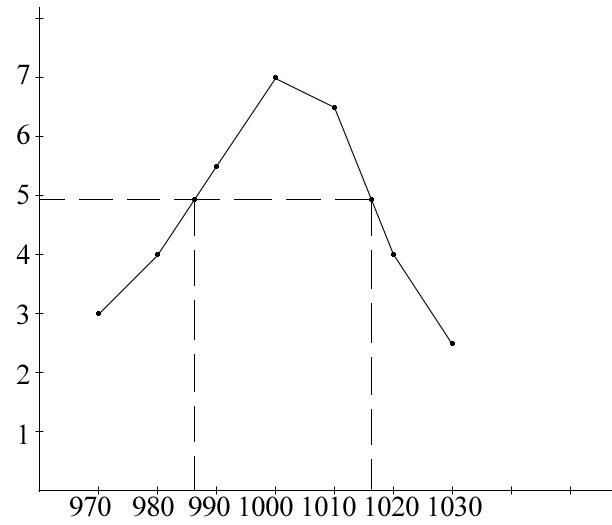
₀=30Гц

6. Расчет времени затухания и добротности резонатора Q=₀/₀

Q=1000/30=33.333

Вывод: Скорости звука полученные при помощи расчетов и эксперементально почти совпадают и равны 347 и 365+39. Разница между ними обусловлена тем, что у нас малое количество измерений, невысокая точность измерений и расчетов.