Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника. Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности. Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности. В любой треугольник можно вписать окружность, причем только одну.

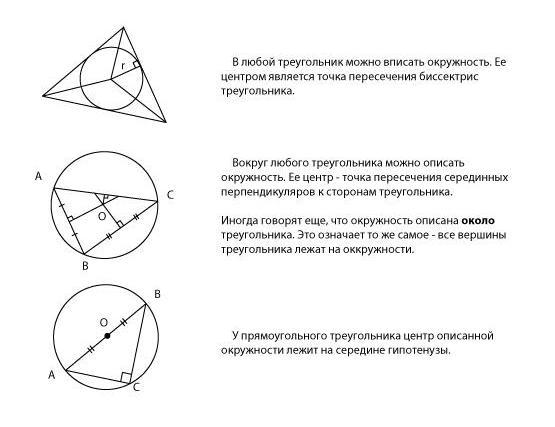
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник. Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

S = p r, где p = (a+b+c) — полупериметр, r — радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части С:

где a, b, c — стороны треугольника, R — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

1. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен а. Тогда гипотенуза равна а . Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда . В ответ запишем .

Ответ: 4.

2. Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, Получаем, что sin C = . Угол С — тупой. Значит, он равен 150°.

Ответ: 150.

3. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

S = ah, где h — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону АВ пополам. По теореме Пифагора найдем h = 32. Тогда R = 25.

EGE-Study » Методические материалы » Геометрия: с нуля до C4 » Вписанные и описанные четырехугольники

Вписанные и описанные четырехугольники

Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Очевидно, эта окружность будет называться описанной вокруг четырехугольника.

Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.

На рисунке — вписанные и описанные четырехугольники и их свойства.

Посмотрим, как эти свойства применяются в решении задач ЕГЭ.

1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Сумма противоположных углов вписанного четырехугольника равна 180°. Пусть угол А равен 82°. Тогда напротив него лежит угол в 98 градусов. Если угол В равен 58°, то угол D равен 180° - 58° = 122°.

Ответ: 122.

2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32.

Пусть сторона АВ равна х, AD равна 2х, а DС — 3х. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, х + 3х = ВС + 2х. Получается, что ВС равна 2х. Тогда периметр четырехугольника равен 8х. Мы получаем, что х = 4, а большая сторона равна 12.

Ответ: 12.

3. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны a и c, а боковые стороны — b и d. По свойству описанного четырехугольника, a + c = b + d, и значит, периметр равен 2(a + c). Получаем, что а + с = 20, а средняя линия равна 10.

Еще раз повторим свойства вписанного и описанного четырехугольника.

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180°.

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

Конец формы