Сумма углов треугольника

Сумма треугольника равна 180 градусов.

Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.

А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.

1. Один из внешних углов треугольника равен 85º. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85°, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение 2х + 3х = 85 и найдем х = 17. Тогда 3х = 51.

Ответ: 51.

2. Один из углов равнобедренного треугольника равен 98º. Найдите один из других его углов. Ответ дайте в градусах.

Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98°?

Нет, конечно! Ведь сумма углов треугольника равна 180°. Значит, один из углов треугольника равен 98°, а два других равны .

Ответ: 41.

3. На рисунке угол 1 равен 46º, угол 2 равен 30º, угол 3 равен 44º. Найдите угол 4. Ответ дайте в градусах.

Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.

Сначала найдем угол 5. Он равен 180° - ∠1 - ∠3 = 90° Тогда ∠6 = 90° ∠7 = 180° - ∠2 - ∠6 = 60°, Угол 4, смежный с углом 7 равен 120°.

Ответ: 120.

Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.

4. Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.

Пусть углы треугольника равны 2х, 3х и 4х. Запишем, чему равна сумма углов этого треугольника. 2х + 3х + 4х = 180° 9х = 180° х = 20° Тогда 2х = 40°.

Ответ: 40.

Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол 1 равен углу А (они накрест лежащие). Угол 2 равен углу С (тоже накрест лежащие). Развернутый угол равен 180º. Значит, и сумма углов треугольника тоже равна 180º.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые а и b. При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

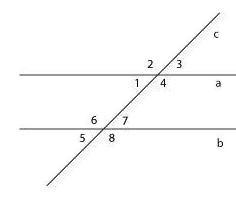
Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть ∠1 = ∠3, ∠2 = ∠4.

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна 180º.

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) — накрест лежащие. Накрест лежащие углы равны. ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна 180°, то есть ∠1 + ∠6 = 180°, ∠4 + ∠7 = 180°.

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.

Соответственные углы равны, то есть ∠2 = ∠6, ∠3 = ∠7.

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

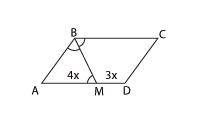
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть ВМ — биссектриса тупого угла В. По условию, отрезки МD и АВ равны 3х и 4х соответственно.

Рассмотрим углы СВМ и ВМА. Поскольку АD и ВС параллельны, ВМ — секущая, углы СВМ и ВМА являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник АВМ — равнобедренный, следовательно, АВ = АМ = 4х.

Периметр параллелограмма — это сумма всех его сторон, то есть 7х + 7х + 4х + 4х = 88. Отсюда х = 4, 7х = 28.

Ответ: 28.

2. Диагональ параллелограмма образует с двумя его сторонами углы 26º и 34º. Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: 120º.

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50º? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, α - β = 50°, то есть α = β + 50°.

Углы α и β — односторонние при параллельных прямых и секущей, следовательно, α + β = 180°.

Итак, 2β + 50° = 180° β = 65°, тогда α = 115°.

Ответ: 115.

EGE-Study » Методические материалы » Геометрия: с нуля до C4 » Высоты, медианы, биссектрисы треугольника