Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

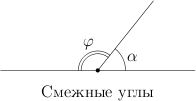
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине  — это угол, смежный с углом . Если угол  острый, то смежный с ним угол — тупой, и наоборот.

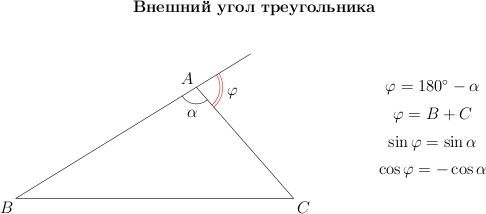
Обратите внимание, что:

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике угол  равен , . Найдите тангенс внешнего угла при вершине .

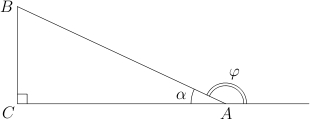
Пусть — внешний угол при вершине . Имеем:

Зная , найдем  по формуле

Получим:

2. В треугольнике угол  равен , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов  и  равна  , . Тогда и синус внешнего угла при вершине  также равен .

Высота в прямоугольном треугольнике

Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач В6 в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и  . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол .

Иными словами, каждый из трех углов треугольника равен одному из углов треугольника и треугольника . Треугольники , и  называются подобными. Давайте нарисуем их рядом друг с другом.

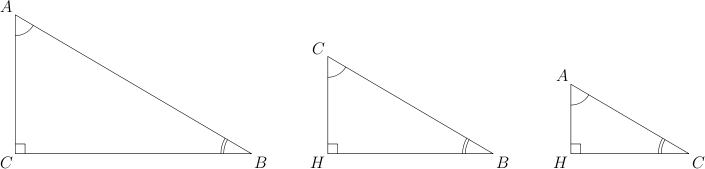
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и  . Стороны треугольника длиннее, чем стороны треугольника , в  некоторое число  раз:

При решении задач нам пригодится равенство углов треугольников , и  , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

1. В треугольнике угол  равен ,  — высота, , . Найдите .

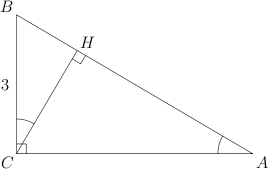
Рассмотрим треугольник . В нем известны косинус угла  и противолежащий катет . Зная синус угла  , мы могли бы найти гипотенузу . Так давайте найдем :

(поскольку значение синуса острого угла положительно). Тогда:

Рассмотрим прямоугольный треугольник , . Имеем:

Отсюда, поскольку :

и тогда

Ответ: .

2. В треугольнике угол  равен , , . Найдите высоту .

Сделайте чертеж и рассмотрите прямоугольный треугольник .

Ответ: .

3. В треугольнике угол  равен , , . К гипотенузе проведена высота . Найдите .

Это чуть более сложная задача. Ведь вам неизвестны катеты  и  .

Зато можно записать теорему Пифагора:

Нам известно также, что

Решая эту систему из двух уравнений, найдем:

Запишем площадь треугольника двумя способами:

и найдем .

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.