стр. 55 из 55

Справочный материал по геометрии.

Два треугольника называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны.

Признаки подобия треугольников.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. стороны одного треугольника пропорциональны сторонам другого.

Признаки подобия прямоугольных треугольников.

Два прямоугольных треугольника подобны, если:

1. они имеют по равному острому углу;

2. катеты одного пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, биссектрисам, медианам.

Отношение периметров подобных треугольников равно коэффициенту подобия этих треугольников. Отношение площадей подобных треугольников равно коэффициенту подобия в квадрате.

Теорема о медиане треугольника (свойство медианы):медиана делит треугольник на два равновеликих треугольника.

Вычисление медианы треугольника, если известны три стороны:

Вычисление высоты треугольника, если известны три стороны:

Вычисление биссектрисы треугольника, если известны три стороны:

!Точка пересечения биссектрис, является центром вписанной окружности в треугольник.

!Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной окружности около треугольника.

Другие теоремы.

Теорема о пропорциональных отрезках: параллельные прямые, пересекающие стороны угла, отсекают на них пропорциональные отрезки.

Теорема о точке пересечения медиан: медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

Теорема о биссектрисе угла треугольника (свойство биссектрисы): биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Отрезок х называется средним пропорциональным (средним геометрическим) между отрезками a и b, если для них выполняется равенство а:х=х:b, т.е. или .

Теорема о пропорциональных отрезках в прямоугольном треугольнике: высота, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу, а катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

1. Окружности.

Теорема о диаметре и хорде: если в круге через внутреннюю точку провести хорду и диаметр, то произведение отрезков хорды равно произведению отрезков диаметра.

Следствие. Если в круге через внутреннюю точку провести несколько хорд, то произведение отрезков каждой хорды есть величина постоянная.

Теорема о касательной и секущей: если из внешней точки провести к кругу касательную и секущую, то квадрат длины отрезка касательной равен произведению отрезка секущей на её внешнюю часть: .

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный . Другими словами, половина развернутого угла.

Острый угол — меньший .

Тупой угол — больший . Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается  . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла  , обозначается  .

Угол обозначается соответствующей греческой буквой .

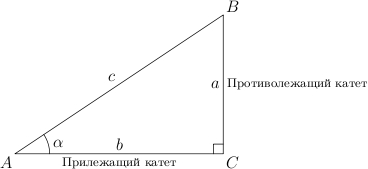
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет  , лежащий напротив угла  , называется противолежащим (по отношению к углу ). Другой катет  , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

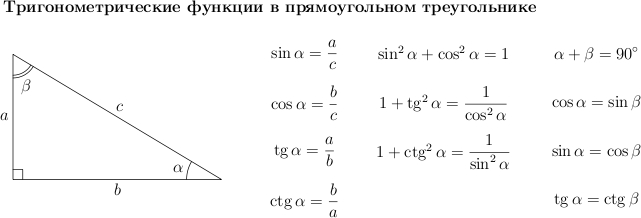
Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa  .

2. С одной сторо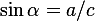ны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла  катет  будет прилежащим.

Получаем, что . Иными словами, .

3. Возьмем теорему Пифагора: 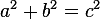. Поделим обе части на :

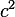Мы получили основное тригонометрическое тождество:

Таким образом, зная синус угла, мы можем найти его косинус, и наоборот.

4. Поделив обе части основного тригонометрического тождества на 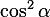 , получим:

Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус.

Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

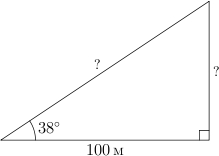
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от   до  .

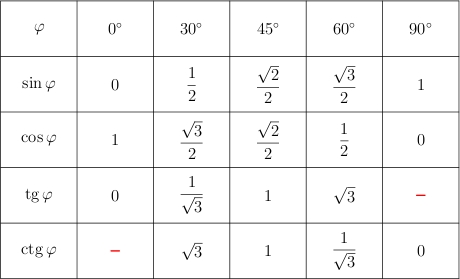
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол  равен  , . Найдите .

Задача решается за четыре секунды.

Поскольку , имеем: .

2. В треугольнике угол  равен  , , . Найдите .

Имеем:

Отсюда

Теперь находим  по теореме Пифагора:

Задача решена.

Часто в задачах встречаются треугольники с углами ,  и   или с углами ,  и  . Основные соотношения для них запоминайте наизусть!

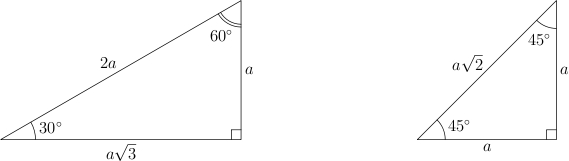
Для треугольника с углами ,  и  катет, лежащий напротив угла в  , равен половине гипотенузы.

Треугольник с углами ,  и   — равнобедренный. В нем гипотенуза в  раз больше катета.