14. Проектування тривимірних об’єктів.

Розглянемо проблему представлення тривимірних зображень на двовимірній площині. Для цього необхідно мати певні математичні моделі. В цих моделях повинні враховуватися різні фактори, які впливають на візуальне сприйняття людиною реальних образів. Спосіб переходу від тривимірних об’єктів до їх зображень на площині будемо називати проекцією. Надалі розглядаються різні види проекцій.

Для того, щоб побачити на площині монітора тривимірне зображення потрібно вміти задати спосіб відображення тривимірних точок в двовимірні. Зробити це можна по-різному. В загальному випадку проекції перетворюють точки, задані в системі координат розмірністю n в точки системи координат розмірністю меншою, ніж n. В нашому випадку точки тривимірного простору перетворюються в точки двовимірного простору. Проекції будуються за допомогою проектуючих променів або проекторів, які виходять з точки, що називається центром проекції. Проектори проходять через площину, яка називається проекційною або картиною площиною і потім проходять через кожну точку тривимірного об’єкта і утворюють тим самим проекцію. Тип проектування на плоску, а не викривлену поверхню, де в якості проекторів використовуються прямі, а не викривлені лінії, називається плоскою геометричною проекцією. Пласкі геометричні проекції поділяються на два види: центральні та паралельні. Якщо центр проекції знаходиться на кінцевій віддалі від проекційної площини, то проекція – центральна. Якщо ж центр проекції віднесений на нескінченність, то проекція – паралельна.

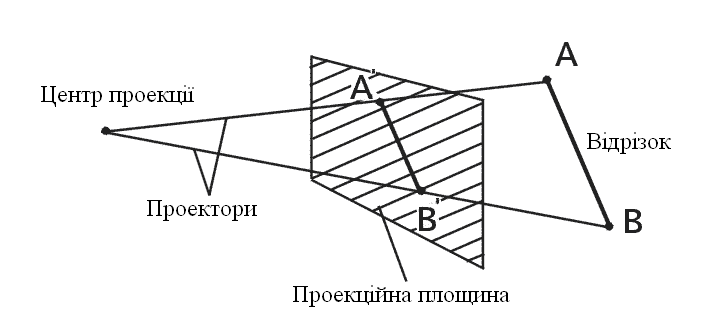
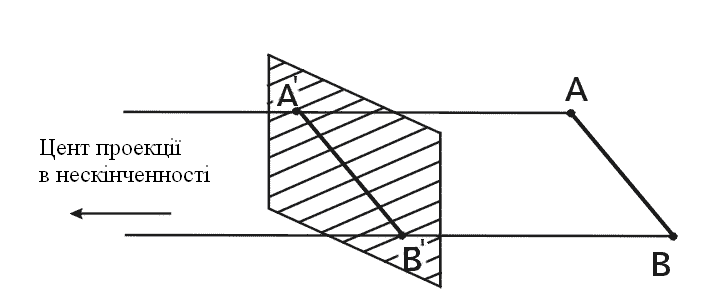
Рис. 14. Центральна проекція. Рис. 15. Паралельна проекція.

Точкою збігу називається точка перетину центральних проекцій довільної сукупності паралельний прямих, які не паралельні проекційній площині. Існує нескінченна множина точок збігу. Точка збігу називається головною якщо сукупність прямих паралельна одній з координатних осей. В залежності від того, скільки координатних осей перетинає проекційну площину розрізняють одно-, двох- і триточкові проекції.

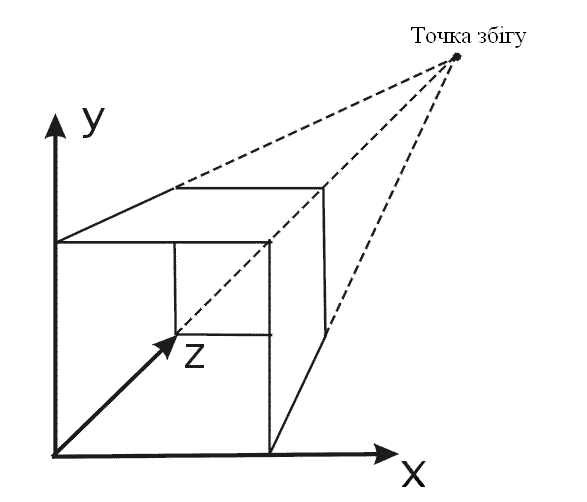
Рис. 16. Одноточкова проекція.

Найпростішою є паралельна прямокутна проекція. В ній сумісно зображаються види зверху, попереду та збоку. Ці проекції часто використовуються в креслені. В залежності від співвідношення між напрямками проектування та нормаллю до проекційної площини паралельні проекції розділяються на ортографічні або ортогональні, в яких ці напрямки співпадають, і косокутні, в яких вони не співпадають. В залежності від положення осей системи координат об’єкта відносно проекційної площини ортографічні проекції поділяються на аксонометричні та ізометричні. В ізометричних проекціях осі системи координат складають одинакові кути з проекційною площиною. В аксонометричних проекціях ці кути різні. Центральна перспективна проекція призводить до візуального ефекту, подібному тому, який дає зорова система людини. При цьому спостерігається ефект перспективного укорочування, коли розмір проекції об’єкта змінюється обернено пропорційно віддалі від центра проекції до об’єкта. В паралельних проекціях відсутнє перспективне укорочування, за рахунок чого зображення отримується менш реалістичним і паралельні прямі завжди залишаються паралельними.

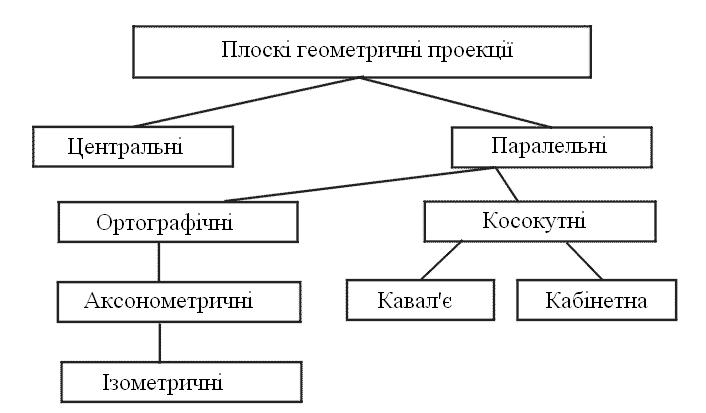
Рис. 17. Типи проекцій.

Розглянемо більш детально центральну перспективну проекцію з математичної точки зору. Для отримання формул центральної перспективної проекції розташуємо осі системи координат, проекційну площину і центр проекції як показано на рис. 18.

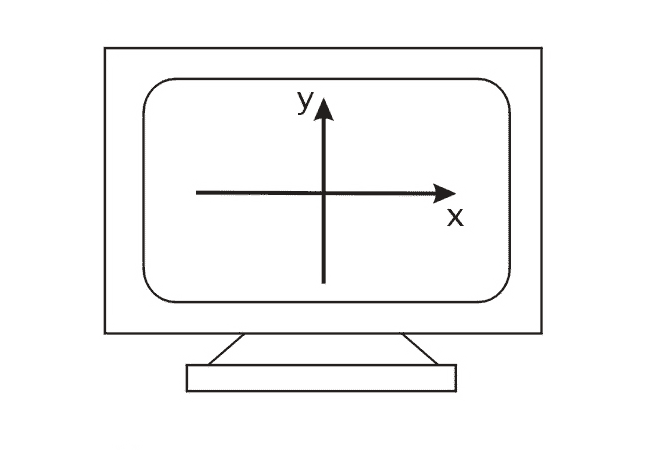
Рис. 18. Розташування осей координат на екрані.

Будемо імітувати на екрані те, що ніби реально знаходиться в просторі за ним. Замітимо, що отрималась лівостороння система координат. Будемо вважати, що площина екрана монітора співпадає з проекційною площиною. Перед тим як переходити до обчислення слід зробити одне важливе зауваження. Оскільки поверхня довільного тривимірного об’єкта містить нескінченну кількість точок, то необхідно задати спосіб опису поверхні об’єкта кінцевою кількістю точок для представлення в комп’ютері. А саме, будемо використовувати лінійну апроксимацію об’єктів в тривимірному просторі за допомогою відрізків прямих і плоских багатокутників. При цьому відрізки прямих після перспективного перетворення переходять у відрізки прямих на проекційній площині. Цю важливу властивість центральної перспективи дозволяє проектувати, тобто робити обчислення тільки для кінцевих точок відрізків, а потім з’єднувати проекції точок лініями вже на проекційній площині.

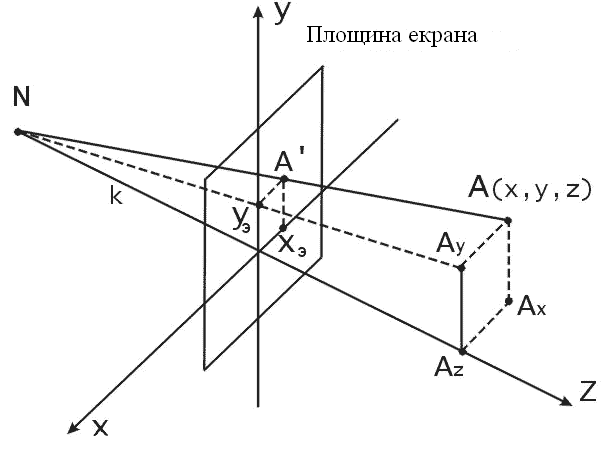
Рис. 19. Вивід формул центральної перспективної проекції.

Точка проектується на екран як . Віддаль від спостерігача до проекційної площини дорівнює k. Необхідно визначити координати точки на екрані. Позначимо їх і . Із подібності трикутників і знаходимо, що

(1)

аналогічно для x: .

Нагадаємо, що k – це віддаль, а спостерігач знаходиться в точці .

Якщо точку спостерігача розмістити в початок координат, а проекційну площину на віддаль , як показано на рис. 20, то формули для і набудуть вигляду:

, (2)

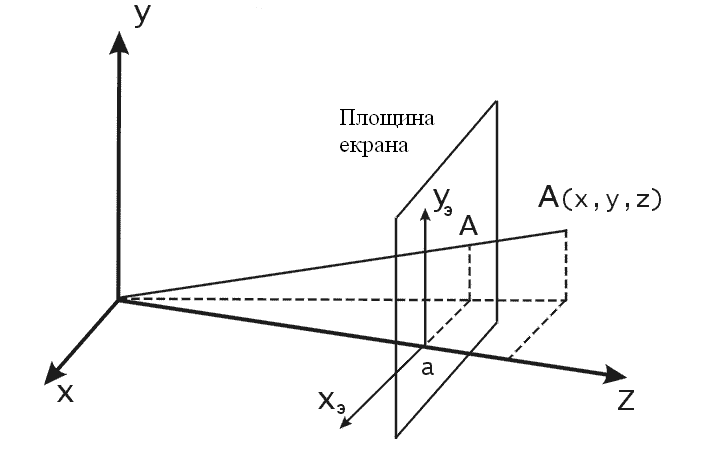
Рис. 20. Інший спосіб обчислення координат точок в центральній перспективній проекції.

Формули (1) більш зручні при необхідності простим чином наближувати або віддаляти спостерігача від проекційної площини. Формули (2) потребують менше часу для обчислення за рахунок відсутності операції додавання.

Розглянемо далі деякі фактори, які впливають на сприйняття людиною тривимірності. Одним із простих способів представлення тривимірних об’єктів є так звані дротяні зображення. Криві лінії при цьому апроксимуються відрізками прямих. Це найбільш швидкий і простий спосіб зображення.

Для підсилення ефекту тривимірної глибини в дротяних зображеннях об’єктів видаляють невидимі лінії. Лінії або їх частини, закриті поверхнями об’єкта, не зображаються. Для цього застосовується спеціальний алгоритм, що потребує вже великих обчислень. Передача глибини може здійснюватися зміною рівня яскравості. Об’єкти, які заходяться ближче до спостерігача, зображаються яскравіше ніж ті, які розташовані далі від нього. Рух об’єктів також дає додатковий ефект глибини. Наприклад, обертання об’єктів навколо вертикальної осі дозволяє відрізняти точки, які знаходяться на різній відділі від осі за рахунок розрізнимості лінійної швидкості обертання точок. Це так званий кінетичний або динамічний ефект глибини.

Більш тонко тривимірність об’єктів може бути представлена за рахунок розрізнимості відбиваючих здатностей поверхонь, їх рельєфу та текстури, а також розрахунку тіней, які відкидають поверхні об’єкта. Одним з ефективних способів досягнення ефекту тривимірності, який рідко використовується, є стереоскопія. При цьому окремо для правого та лівого ока спостерігача формуються зображення, які не сильно відрізняються один від одного, подібно тому, як це відбувається в реальності. Це викликає так званий бінокулярний ефект, який полягає в тому, що наш мозок зливає два окремих образа в один, який інтерпретується як тривимірний. Ці два окремих зображення називаються стереопарою.

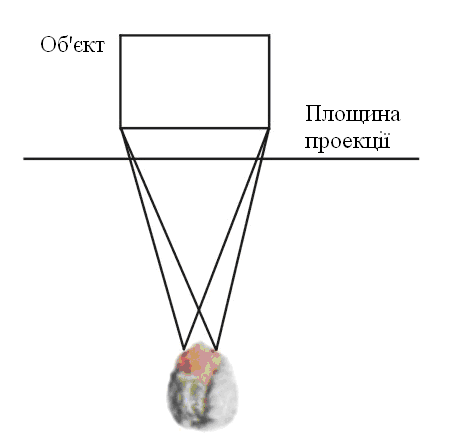
Рис. 21. Бінокулярний ефект, стереоскопія.

Технічно цей метод реалізується, наприклад, за допомогою окулярів із спеціальними поляризованими стеклами. На екран монітора почергово виводяться зображення для лівого та правого ока. А скло окулярів стають почергово, відповідно, прозорими або непрозорими. При достатньо частій зміні зображень зміни станів прозорості і непрозорості не відчувається. Оскільки при зміні положення голови центр проекції залишається на місці, то створюється псевдо-тривимірний ефект. Синхронізація зміни кадрів на екрані та поляризації лінз окулярів відбувається за допомогою спеціальних датчиків, розташованих на окулярах і моніторі.