
- •Введение
- •Глава 1 знакомство с matlab и простейшие вычисления
- •1.1. Рабочая среда matlab
- •1.2. Арифметические вычисления
- •1.3. Вещественные числа
- •1.4. Форматы вывода результата вычислений
- •1.5 Комплексные числа
- •1.6 Векторы и матрицы
- •1.7 Встроенные функции. Функции, задаваемые пользователем
- •1.8 Сообщения об ошибках и их исправление
- •1.9 Просмотр и сохранение переменных
- •1.10 Матричные и поэлементные операции над векторами и матрицами
- •1.11 Решение систем линейных уравнений
- •Вопросы для самопроверки
- •Глава 2 работа с массивами
- •2.1 Создание векторов и матриц
- •2.2 Применение команд обработки данных к векторам и матрицам
- •2.3 Создание специальных матриц
- •2.4 Создание новых массивов на основе существующих
- •Вопросы для самопроверки
- •Глава 3 м-файлы
- •3.1 Файл-программы
- •3.2 Файл-функции
- •Вопросы для самопроверки
- •Глава 4 программирование
- •4.1 Операторы отношения и логические операторы
- •4.2 Операторы цикла
- •4.3 Операторы ветвления
- •4.4 Оператор переключения switch
- •4.5 Оператор прерывания цикла break
- •4.6 Пример сравнения быстродействия матричных и скалярных операций
- •Вопросы для самопроверки
- •Глава 5 высокоуровневая графика
- •5.1 2D графика
- •5.1.1 Графики в линейном масштабе
- •5.2 Специальные виды 2d - графиков
- •5.2.1 Представление функции в виде дискретных отсчетов
- •5.2.2 Лестничные графики
- •5.2.3 Графики с указанием погрешности
- •5.2.4 Графики в логарифмическом и полулогарифмическом масштабах
- •5.2.5 Графики параметрических функций
- •5.3 3D графика
- •5.3.1 Линейчатые поверхности
- •5.3.2 Каркасные поверхности
- •5.3.3 Контурные графики
- •5.3.4 Сплошная освещенная поверхность
- •5.4.2 Сохранение и экспорт графиков
- •5.4.3 Анимация
- •Вопросы для самопроверки
- •Глава 6 прикладная численная математика
- •6.1 Операции с полиномами
- •6.2 Решение уравнений и их систем
- •6.3 Минимизация функции одной переменной
- •6.4 Минимизация функции нескольких переменных
- •6.5 Вычисление определенных интегралов
- •6.6 Решение дифференциальных уравнений
- •Вопросы для самопроверки
- •Глава 7 символьные вычисления
- •7.1 Символьные переменные, константы и выражения
- •7.2 Вычисления с использованием арифметики произвольной точности
- •7.3 Команды упрощения выражений – simplify, simple
- •7.4 Команда расширения выражений – expand
- •7.5 Разложение выражений на простые множители – команда factor
- •7.6 Приведение подобных членов – команда collect
- •7.7 Обеспечение подстановок – команда subs
- •7.8 Вычисление пределов – команда limit
- •7.9 Вычисление производных – команда diff
- •7.10 Вычисление интегралов – команда int
- •7.11 Разложение в ряд Тейлора – команда taylor
- •7.12 Вычисление суммы ряда – команда symsum
- •7.13 Решение уравнений и их систем – команда solve
- •7.14 Решение дифференциальных уравнений – команда dsolve
- •7.15 Прямое и обратное преобразования Лапласа – команды laplace, ilaplace
- •7.16 Графики символьных функций – команды ezplot, ezpolar
- •7.17 Прямой доступ к ядру системы Maple – команда maple
- •7.18 Разложение рациональной дроби на сумму простейших дробей
- •7.20 Решение неравенств и систем неравенств
- •7.21 Разложение в ряд Тейлора функции нескольких переменных
- •7.22 Решение дифференциальных уравнений с помощью степенных рядов
- •7.23 Решение тригонометрических уравнений
- •Вопросы для самопроверки
- •Приложения Приложение 1. Справочная система matlab
- •Приложение 2. Знакомство с пакетами расширения системы matlab
- •Приложение 3. Задания для самостоятельной работы
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Варианты
- •Литература
Варианты
1.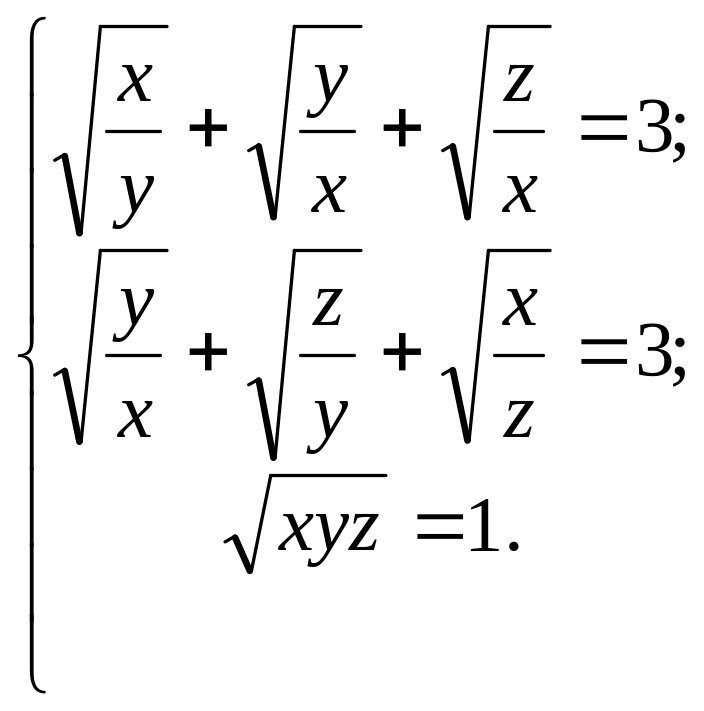 2.
2.![]() 3.
3.![]() 4.
4.![]()
5.![]() 6.
6.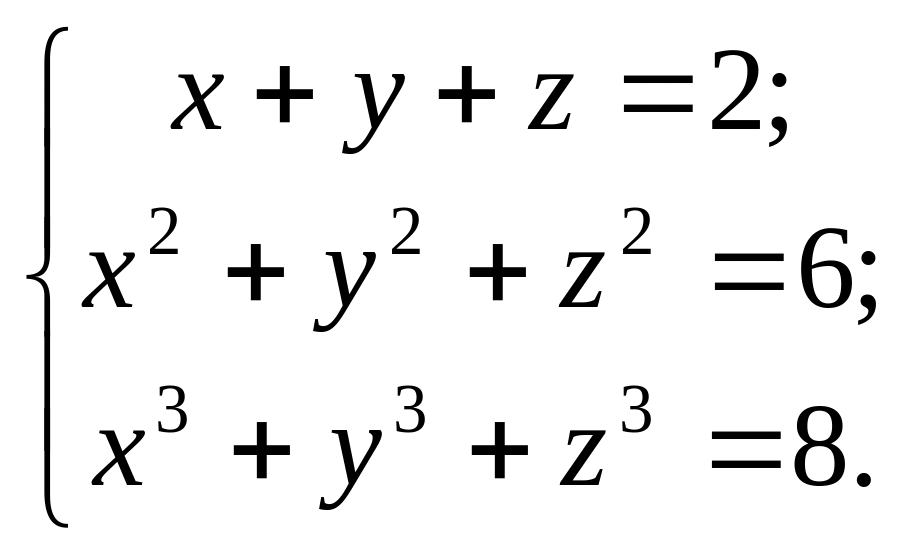 7
7![]() 8.
8.
![]()
9.
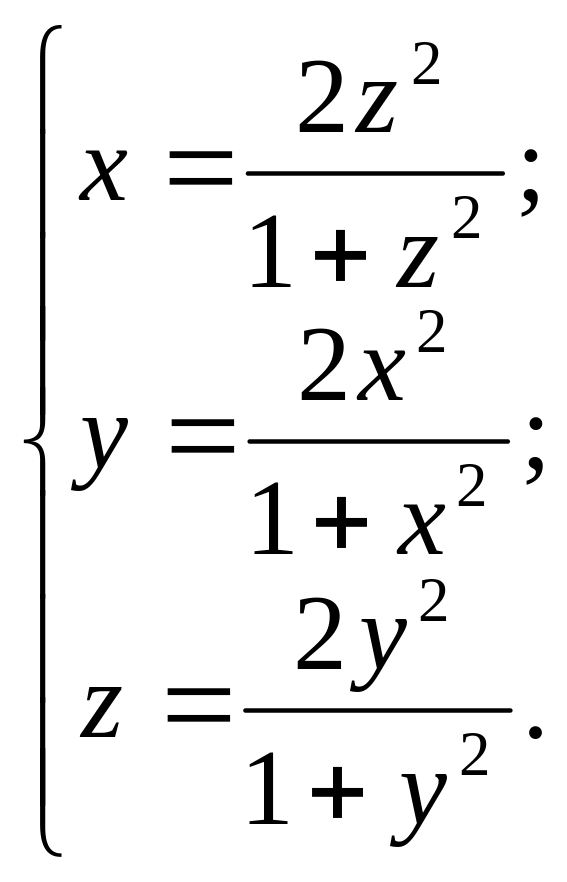 10
10![]() 11.
11.![]() 12.
12.![]()
13.![]() 14.
14.![]() 15.
15.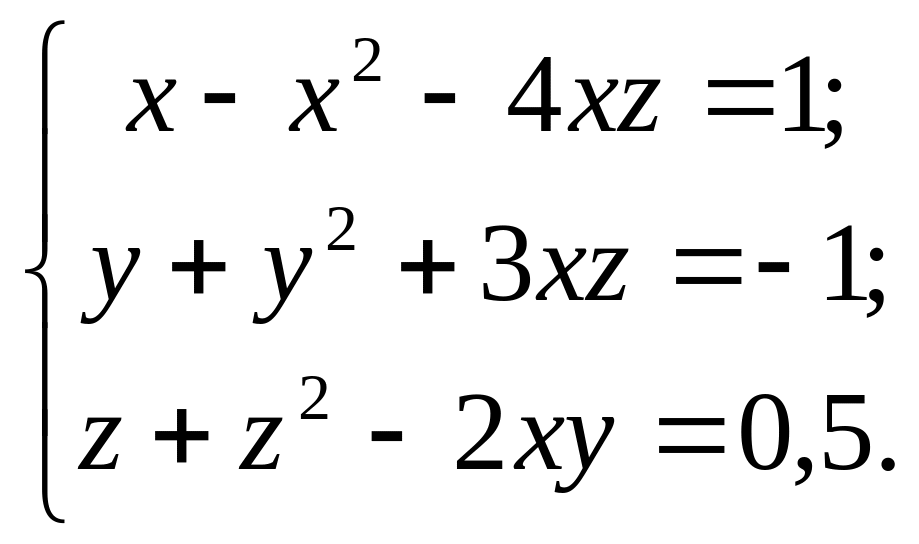
Задание 31 (7.14). Решить дифференциальное уравнение или
систему дифференциальных уравнений
Решить с помощью команды dsolve дифференциальное уравнение или
систему дифференциальных уравнений. Воспользоваться при необходимости командами pretty, simple. Проверить решение
подстановкой.
Варианты
1.
y′′-4y′+4y=xe2x 2.
y′′+9y=exscosx
3.
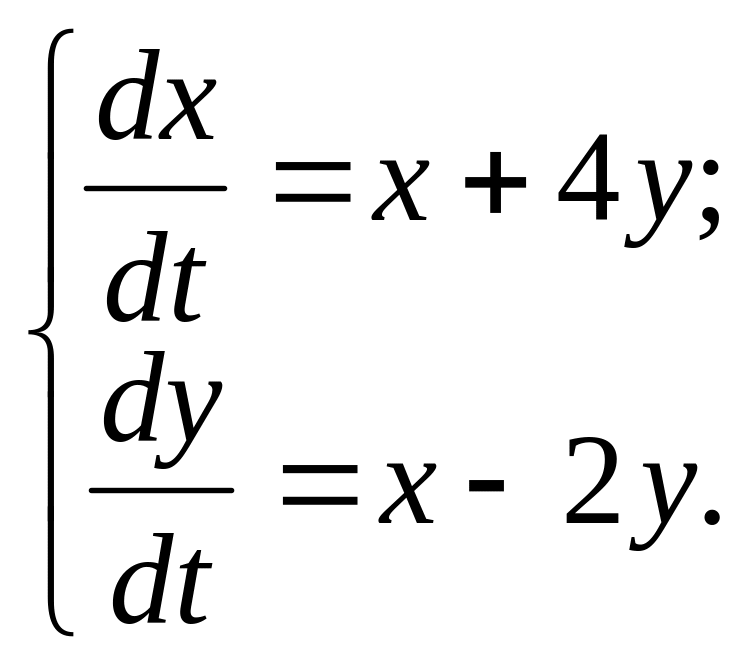 4.
y′′-2y=
4.
y′′-2y=![]()
5.
y′′+y=tg2x,
y(0)=2,
y′(0)=1
6.
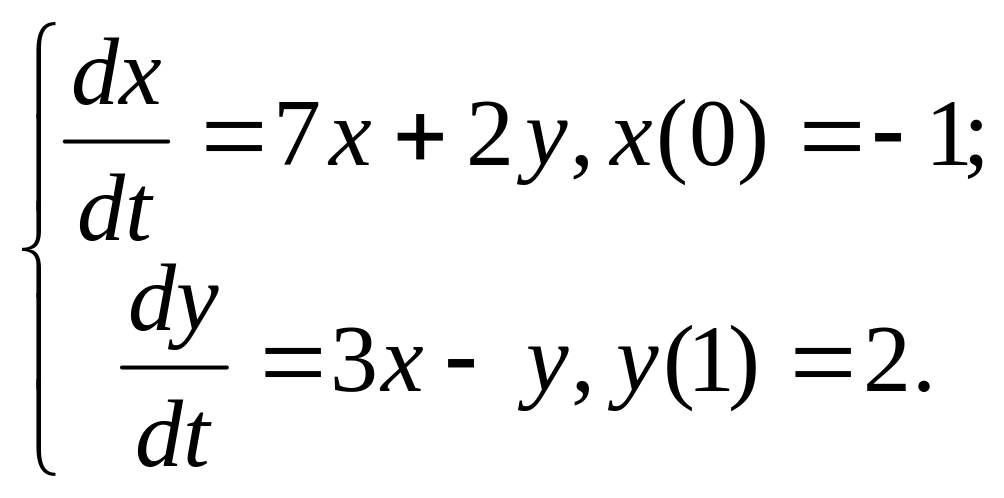 7.
y′′-y′=e2xscosex
7.
y′′-y′=e2xscosex
8.
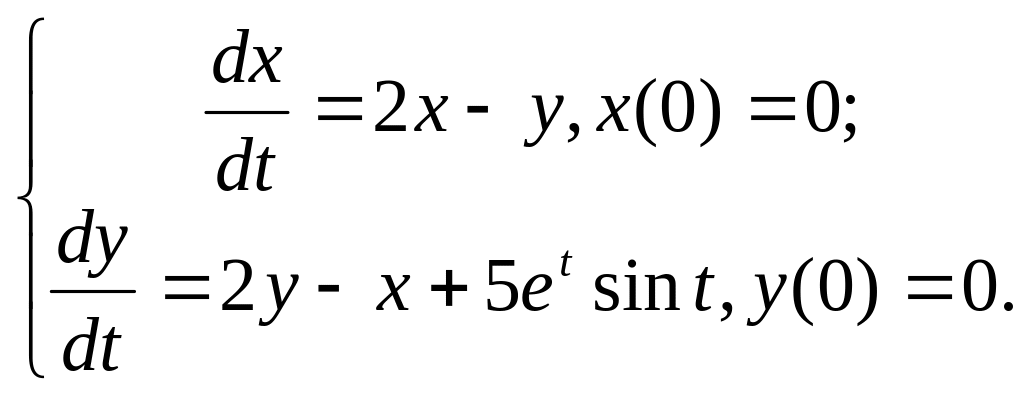 9.
y(5)–y'''
= x2–1
10.
y(4)–y
= 5exsinx+x4
9.
y(5)–y'''
= x2–1
10.
y(4)–y
= 5exsinx+x4
11. y'''−3y′=3(2-x2),
y(0)=1, y′(0)=1,
y′′(0)=1 12.
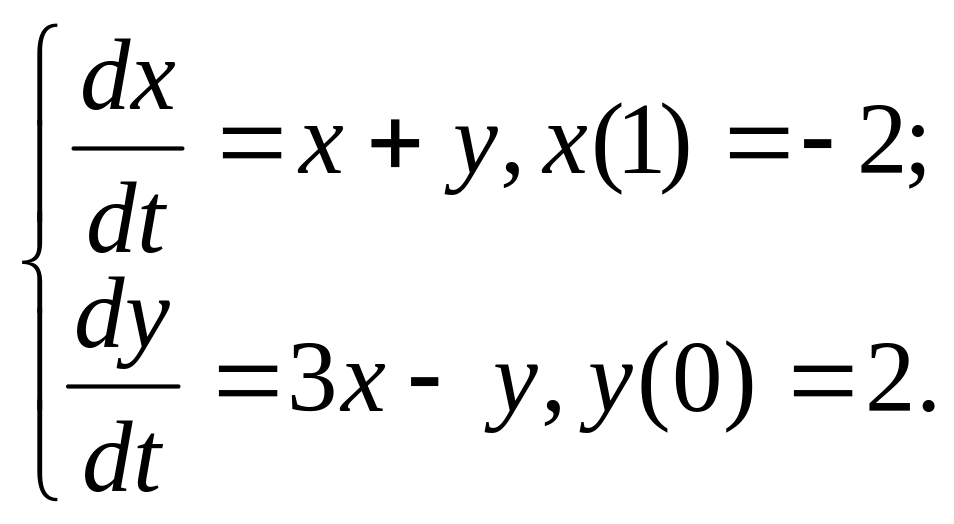
13. y′′+4y=![]() y(0)=0, y′(0)=1
14.
y(0)=0, y′(0)=1
14.
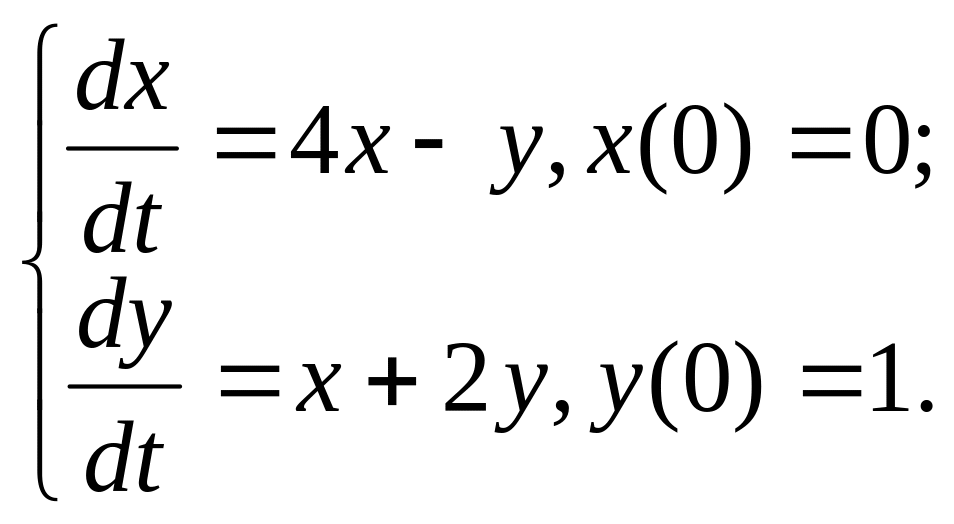
15. y(5)+4y''' = ex+3sin2x+1
Литература
1. Ануфриев И.Е. Самоучитель MATLAB 5.3/6.x. – СПб.: БХВ - Петербург, 2003. – 736 с.
2. Гультяев А.К. MATLAB 5.3. Имитационное моделирование в среде Windows. Практическое пособие. – СПб.: Корона принт, 2001. – 432 с.
3. Дьяконов В.П. MATLAB: учебный курс. – СПб.: Питер, 2001. – 560 с.
4. Дьяконов В.П. Компьютерная математика. Теория и практика. – М.: «Нолидж», 2001. – 1296 с.
5. Дьяконов В.П., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. – СПб.: Питер, 2001. – 480 с.
6. Курбатова Е.А. MATLAB 7. Самоучитель. – М.: Издательский дом "Вильямс", 2006. – 256 с.
7. Кетков Ю.Л., Кетков А.Ю., Шульц М. М. MATLAB 6.x.:программирование численных методов. – СПб.: БХВ-Петербург, 2004. – 672 с.
8. Лазарев Ю.Ф. MATLAB 5.x. – Киев.: BHV, 2000. – 384 с.
9. Мартынов Н.Н. MATLAB 7. Элементарное введение. – М.: КУДИЦ - ОБРАЗ, 2005. – 416 с.
10. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.: БХВ - Петербург, 2001. – 528 с.
11. Мэтьюз Дж. Г., Финк К.Д. Численные методы. Использование MATLAB: Пер. с англ. – М.: Издательский дом "Вильямс", 2001. – 713 с.
12. Новгородцев А.Б. Расчет электрических цепей в MATLAB: Учебный курс. – СПб.: Питер, 2004. – 250 с.
13. Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ-Петербург, 2005. – 320 с.
14. Поршнев С.В. MATLAB 7. Основы работы и программирования. Учебник – М.: ООО «Бином - Пресс», 2006. – 320 с.
15. Потемкин В.Г. Инструментальные средства MATLAB 5.x. – М.: Диалог - МИФИ, 2001. – 324 с.
16. Brian R. Hunt, Ronald L. Lipsman, Jonathan M. Rosenberg with Kevin R. Coombes, John E. Osborn, Garret J. Stuck. Matlab. Официальный учебный курс Кембриджского университета. – М.: Изд-во ТРИУМФ, 2008. – 352 с.
