4.3 Неявна схема
Розглянемо неявну дев'яти точкову схему з ваговими коефіцієнтами й запишемо відповідне різницеве рівняння:
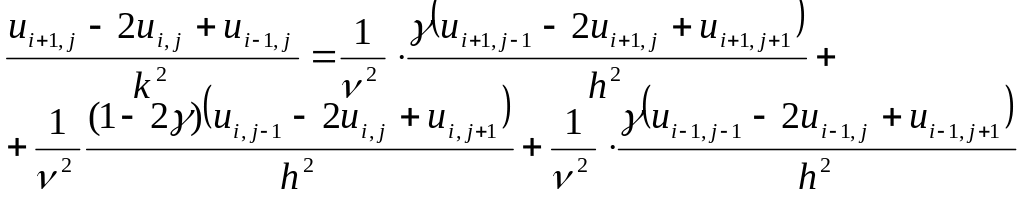
Після перетворень та вразовуючи граничні умови, отримуємо таку систему лінійних алгебраїчних рівнянь для кожного часового шару, починаючи з третього:
Значення розв'язку на перших двох шарах обчислюємо з початкових умов та за формулою (4.4). Систему можно розв'язувати методом прогону, який буде стійким, тому що має місце діагональна перевага.
Зазвичай
обирають
.
Тоді схема є абсолютно стійкою. Коли
схема перетворюється у схему хрест, а
умова стійкості на умову
.
4.4 Задача для самостійного розв'язку на практиці
Задача 4.1. Знайти розв'язок крайової задачі для рівняння
,
,
с
початковими умовами:
,
і
граничними умовами:
,
.
Завдання до лабораторної роботи
Завдання
4.1.
Використовуючи метод сіток, розв'язати
змішану задачу для рівняння коливання
струни
з початковими умовами
,
,
,
і крайовими умовами
,
.
Розв'язок виконати із кроком
;
.
Знайти
наближений розв'язок задачі за допомогою
явної різницевої схеми. Виконати
розрахунки з половинним кроком за часом
і довжині струни й оцінити точність
отриманого розв'язку.
Завдання 4.2. Знайти наближений розв'язок задачі завдання 4.1 за допомогою неявної різницевої схеми. Порівняти отримані результати.
Варіанти індивідуальних завдань
1.
|
2.
|
3.
|
4.
|
5.
|
6.
,
|
7.
|
8.
|
9.
|
10.
,
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
,
|
19.
|
20.
|
|
,
,
,
.
,
,
,
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
,
,
,
,
,
,
,
,
,
,
.
Завдання
4.3.
Коливання
тонкої пластини, якщо не враховувати
втрати на тертя, описуються нормованим
хвильовим рівнянням виду:
,
де
– деформація пластини,
– координати,
– час. Розрахуйте коливання при заданих
у таблиці розмірах
і
,
граничних
,
,
,
і початкових
і
умовах. Використовувати
PDE Tools пакета MATLAB.
Варіанти індивідуальних завдань
Параметр |
Варіант |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
||
, см |
1 |
2 |
3 |
2 |
3 |
2 |
|
, см |
2 |
1 |
2 |
3 |
1 |
2 |
|
Граничні умови |
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
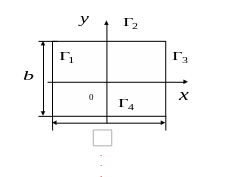
Рисунок 4.7 – Область розв'язку завдання 4.3