
- •Чисельні методи
- •5 Методи розв'язку інтегральних рівнянь
- •1 Пакет pde Tools решения задач для уравнений в частных производных
- •1.2. Выполнение расчетов в пакете matlab
- •1.3 Задачи для самостоятельного решения
- •2 Метод сіток розв'яЗання еліптичних рівнянь
- •2.1 Метод сіток – постановка задачі
- •2.2 Побудова сітки й апроксимація рівняння
- •2.4 Погрішність вирішення й збіжність
- •2.5 Задача для самостійного вирішення на практиці
- •2.6. Завдання до лабораторної роботи
- •3 Метод сіток
- •3.1 Постановка задачі
- •3.2 Явна різницева схема
- •3.3 Неявна різницева схема
- •3.4 Різницеві схеми підвищеної точності. Схема Кранка-Нікольсона
- •3.5 Задачі для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •3.7 Контрольні питання
- •4 Метод сіток розв'язку крайових задач для хвильових рівнянь
- •4.1 Постановка задачі
- •Явна схема
- •4.3 Неявна схема
- •4.4 Задача для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •4.6 Контрольні питання
- •5 Методи розв'язку інтегральних рівнянь
- •5.1 Загальні відомості про інтегральні рівняння
- •5.2 Метод послідовних наближень розв'язку інтегральних рівнянь Фредгольма
- •5.3 Квадратурний метод розв'язку інтегральних рівнянь Фредгольма
- •5.4 Загальні відомості про інтегральні рівняння Вольтерра
- •5.5 Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра
- •5.6 Квадратурний метод розв'язку інтегральних рівнянь Вольтерра
- •5.7 Завдання до лабораторної роботи
- •5.8 Контрольні питання
- •6 Література
3.3 Неявна різницева схема
Для апроксимації диференціального рівняння використовуємо нижній шаблон рисунка 3.1. Тобто, вважаємо, що вираз (3.2) апроксимує похідну за часом у момент . Тоді й другу похідну по х в (3.3) беремо в тому ж часовому шарі. Схема відповідає нижньому шаблону, наведеному на рисунку 3.1.
Маємо таку апроксимацію диференціального рівняння:
![]() (3.7)
(3.7)
Вираження
(3.7) записується для кожного внутрішнього
вузла стрижня і являє собою систему
лінійних алгебраїчних рівнянь для
невідомих значень температури в момент
часу
.
Кожне рівняння системи містить три
невідомі, тобто система є трьох
діагональною, і може бути вирішена
методом прогону або Lu-розкладання.
Додамо до системи граничні умови й
запишемо систему в канонічному виді
(позначимо
![]() ):
):
![]()
Система має діагональну перевагу, тому прогін стійкий.
Така схема стійка без яких небудь додаткових обмежень на узгодження кроків за часом і координаті x. Розмір кроків визначається тільки вимогами точності отриманого розв'язку.
Оскільки
має місце апроксимація крайової задачі
порядку
![]() й стійкість, то буде мати місце збіжність
розв'язку різницевої задачі до розв'язку
вхідної задачі:
й стійкість, то буде мати місце збіжність
розв'язку різницевої задачі до розв'язку
вхідної задачі:
![]()
Порядок
апроксимації по х
крайової задачі зменшився на 1 за рахунок
апроксимації похідної у другій крайовій
умові. Якщо на правому кінці задаються
значення функції, то порядок апроксимації
крайової задачі буде
![]() .
.
Апостеріорна оцінка погрішності може бути отримана за правилом Рунге на основі подвійного прорахунку за формулою (2.7). Використовуючи екстраполяцію Ричардсона можна уточнити отриманий розв'язок, підвищивши порядок точності розв'язку на 1 (формула 2.8).
3.4 Різницеві схеми підвищеної точності. Схема Кранка-Нікольсона
Різницеві схеми підвищеної точності будуються за шаблонами, що викоритстовують більше точок, що дозволяє підвищити порядок апроксимації диференціальної задачі різницевою схемою.
Схема Кранка-Нікольсона будується за шеститочковим шаблоном і має вигляд:
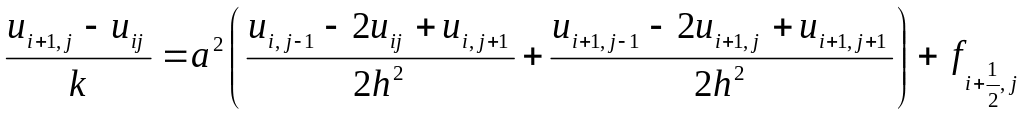
Порядок
апроксимації цієї схеми
![]() .
Схема є абсолютно стійкою, тобто кроки
.
Схема є абсолютно стійкою, тобто кроки
![]() та
обираються тільки з умов досягнення
необхідної точності.
та
обираються тільки з умов досягнення
необхідної точності.
Покажемо,
чому апроксимація за часом має другий
порядок точності. Для цього розкладемо
функцію
![]() в ряд Тейлора в точці
в ряд Тейлора в точці
![]() .
Позначимо
.
Позначимо
![]() .
.
![]()
![]()
Звідки отримуємо
![]() .
.
3.5 Задачі для самостійного розв'язку на практиці
Задача
3.1.
Перевірити, що функція
![]() є розв'язком рівняння
є розв'язком рівняння
![]() для кожного позитивного числа
для кожного позитивного числа
![]()
Задача
3.2. Розв'язати
задачу розподілу тепла в стрижні довжини
1, тобто розв'язати рівняння
![]() при
при
початковій
умові: ![]() ,
,
граничних
умовах
![]() .
.
Розрахунки
виконати до моменту часу
![]() .
Розв'язати по явній і неявній схемі й
порівняти результати.
.
Розв'язати по явній і неявній схемі й
порівняти результати.
Завдання до лабораторної роботи
Завдання
3.1.
Використовуючи метод сіток одержати
розв'язок змішаної задачі для
диференціального рівняння параболічного
типу
![]() (рівняння теплопровідності) при заданих
початкових і граничних умовах
(рівняння теплопровідності) при заданих
початкових і граничних умовах
![]() ,
,![]() ,
,![]() ,
де
,
де
![]() .
Розв'язок виконати при
.
Розв'язок виконати при![]() ,
крок за часом підібрати з умови стійкості.
Знайти
наближений розв'язок задачі за допомогою
явної різницевої схеми. Повторити
розрахунки з половинним кроком по
координаті, вибравши відповідний крок
за часом, зрівняти отримані результати
й одержати оцінку погрішності розв'язку.
,
крок за часом підібрати з умови стійкості.
Знайти
наближений розв'язок задачі за допомогою
явної різницевої схеми. Повторити
розрахунки з половинним кроком по
координаті, вибравши відповідний крок
за часом, зрівняти отримані результати
й одержати оцінку погрішності розв'язку.
Завдання 3.2. Знайти наближений розв'язок задачі завдання 5.1 за допомогою неявної різницевої схеми. Порівняти отримані розв'язки й об'єм обчислень, необхідних для одержання розв'язку з тою ж точністю.
Варіанти індивідуальних завдань
1.
![]() ,
,![]() ,
,
![]() .
.
2.
![]() ,
,![]() ,
,
![]() .
.
3.
![]() ,
,![]() ,
,
![]() .
.
4.
![]() ,
,![]() ,
,
![]() .
.
5.
![]() ,
,
,
,
![]() .
.
6.
![]() ,
,![]() ,
,
![]() .
.
7.
![]() ,
,![]() ,
,
![]() .
.
8.
![]() ,
,![]() ,
,
![]() .
.
9.
![]() ,
,![]() ,
,
![]() .
.
10.
![]() ,
,![]() ,
,
![]() .
.
11.
![]() ,
,![]() ,
,
![]() .
.
12.
![]() ,
,![]() ,
,
![]() .
.
13.
![]() ,
,![]() ,
,
![]() .
.
14.
![]() ,
,![]() ,
,
![]() .
.
15.
![]() ,
,![]() ,
,
![]() .
.
16.
![]() ,
,
.
,
,
.
17.
![]() ,
,![]() ,
,
![]() .
.
18.
![]() ,
,![]() ,
,
![]() .
.
19.
![]() ,
,![]() ,
,
![]() .
.
20.
![]() ,
,![]() ,
,
![]() .
.
Завдання 3.3. Розв'язати двовимірну крайову задачу:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
за допомогою PDE Tools пакета MATLAB. Розв'язок задачі вивести у вигляді анімації.
Варіанти індивідуальних завдань
Параметр |
Варіант |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
|
, см |
1 |
2 |
3 |
2 |
3 |
2 |
, см |
2 |
1 |
2 |
3 |
1 |
2 |
|
0,2 |
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
|
|
|
|
|||
|
|
|
0 |
|||
|
0 |
|
0 |
|||
|
|
0 |
|
|||
|
0 |
0 |
|
|||
