
- •Чисельні методи
- •5 Методи розв'язку інтегральних рівнянь
- •1 Пакет pde Tools решения задач для уравнений в частных производных
- •1.2. Выполнение расчетов в пакете matlab
- •1.3 Задачи для самостоятельного решения
- •2 Метод сіток розв'яЗання еліптичних рівнянь
- •2.1 Метод сіток – постановка задачі
- •2.2 Побудова сітки й апроксимація рівняння
- •2.4 Погрішність вирішення й збіжність
- •2.5 Задача для самостійного вирішення на практиці
- •2.6. Завдання до лабораторної роботи
- •3 Метод сіток
- •3.1 Постановка задачі
- •3.2 Явна різницева схема
- •3.3 Неявна різницева схема
- •3.4 Різницеві схеми підвищеної точності. Схема Кранка-Нікольсона
- •3.5 Задачі для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •3.7 Контрольні питання
- •4 Метод сіток розв'язку крайових задач для хвильових рівнянь
- •4.1 Постановка задачі
- •Явна схема
- •4.3 Неявна схема
- •4.4 Задача для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •4.6 Контрольні питання
- •5 Методи розв'язку інтегральних рівнянь
- •5.1 Загальні відомості про інтегральні рівняння
- •5.2 Метод послідовних наближень розв'язку інтегральних рівнянь Фредгольма
- •5.3 Квадратурний метод розв'язку інтегральних рівнянь Фредгольма
- •5.4 Загальні відомості про інтегральні рівняння Вольтерра
- •5.5 Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра
- •5.6 Квадратурний метод розв'язку інтегральних рівнянь Вольтерра
- •5.7 Завдання до лабораторної роботи
- •5.8 Контрольні питання
- •6 Література
1.2. Выполнение расчетов в пакете matlab
Пакет MATLAB содержит приложение PDE Toolbox (от англ. Partial Differential Equation – дифференциальное уравнение в частных производных). Приложение обеспечивает решение дифференциальных уравнений в частных производных методом конечных элементов в двухмерной постановке. Оно включает графический интерфейс; инструменты задания формы уравнений и граничных условий; процедуру автоматической генерации сетки конечных элементов; средства для визуализации полученного решения и его анимации. PDE Toolbox использует проекционную формулировку метода конечных элементов.
PDE Toolbox представляет собой набор специальных функций, написанных на языке MATLAB. Особое место среди всех функций PDE Toolbox занимают pdetool и pdeinit. При вызове этих функций из рабочего окна MATLAB разворачивается графический интерфейс, обеспечивающий решение задачи.
Пример
1.1. Решить
задачу о ламинарном установившемся
движении вязкой жидкости по призматическому
каналу (рис.1.1). Канал имеет свободную
поверхность и зазор между призматическими
поверхностями. Характеристики канала:
![]() м,
м,
![]() м,
м,
![]() м,
м,
![]() м. Движение жидкости описывается
уравнением Пуассона:
м. Движение жидкости описывается
уравнением Пуассона:
![]() ,
,
где
![]() – продольная скорость,
– продольная скорость,
![]() – градиент давления вдоль оси канала,
– градиент давления вдоль оси канала,
![]() – кинематическая вязкость. Граничные
условия:
– кинематическая вязкость. Граничные
условия:
условие прилипания на границе канала:
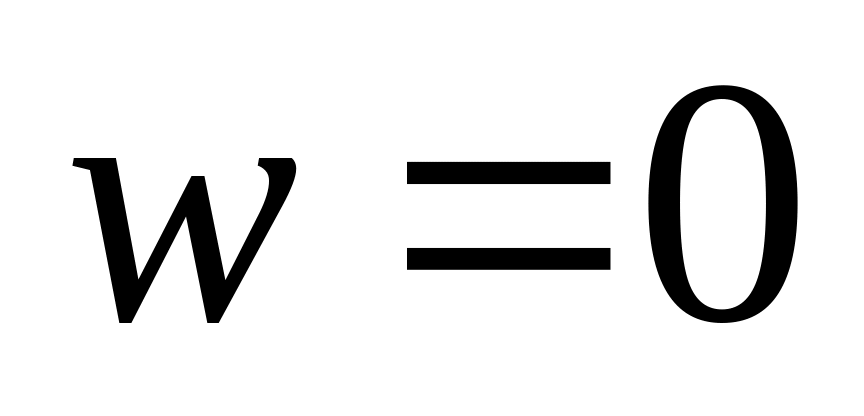 ;
;
условие отсутствия трения (если есть свободная поверхность):
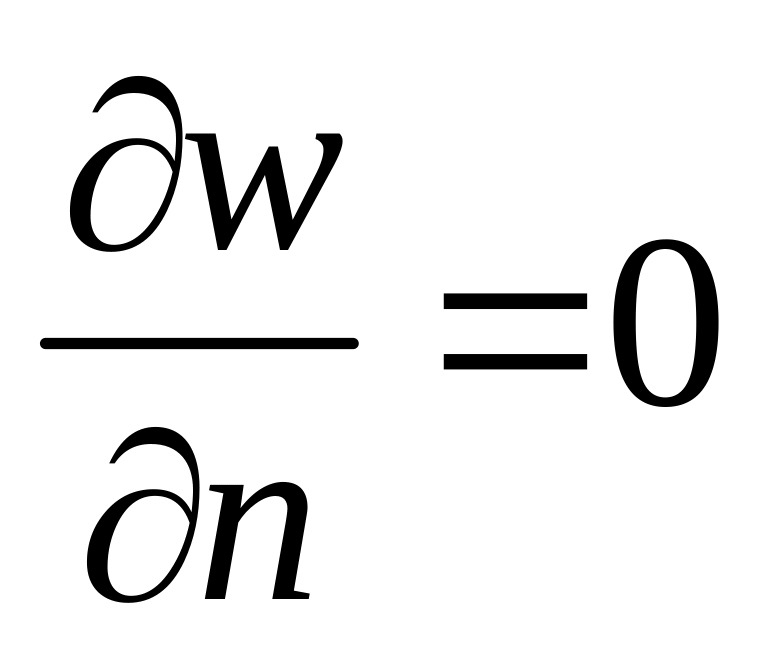 ,
где
– нормаль к поверхности.
,
где
– нормаль к поверхности.
Решить
задачу для случая, когда
![]() .
.

![]()
![]()




![]()


![]()
![]()
Рисунок 1.1 – Призматический канал
Решение.
Математическая постановка задачи (рис. 1.2):
Характеристики:
![]() ,
,
![]() ,
,
,
.
,
,
,
.
Решить уравнение:
![]() ,
,
Граничные условия:
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Рисунок 1.2 – Математическая постановка задачи
З а п у с к п р и л о ж е н и я PDE Toolbox приводит к появлению на экране окне графического интерфейса, изображённого на рис. 1.3. Для этого в командной строке набираем:
>> pdetool
В верхней части интерфейса располагается строка главного меню, включающего пункты "File", "Edit" и другие. Непосредственно под главным меню размещена панель, включающая инструменты PDETool, список видов задач "Application" и указатель значений координат x и y. Ниже расположены окно "Set formula" (ввод формулы) и собственно графическое окно для работы с изображением расчётной области. Внизу имеется информационная строка “Info” и кнопка "Exit" (выход).
Н а п е р в о м э т а п е решения необходимо сформировать исходную геометрию задачи в графическом окне интерфейса PDETool.
Изображения формируются с помощью команд пункта Draw (Рисовать) главного меню:
Draw Mode – переключение в режим ввода (прорисовки) геометрии;
Rectangle/square – ввод прямоугольника или квадрата с помощью мыши начиная от его верхней левой вершины;
Rectangle/square (centered) – ввод прямоугольника или квадрата с помощью мыши начиная от его центра;
Ellipse/circle – ввод эллипса или круга с помощью мыши начиная от верхней левой точки;
Ellipse/circle (centered) – ввод эллипса или круга с помощью мыши начиная от центра;
Polygon – прорисовка многоугольника отрезками ломаной линии, пока она не станет замкнутой;
Rotate – поворот выделенных объектов вокруг некоторой точки;
Export Geometry Description, Set Formula, Labels… – экспорт в базовую рабочую область MATLAB переменных описания геометрии.
Для того, чтобы установить размерности области данной задачи, нужно в меню Option выбрать Axes Limits… В строке X-axis range набрать [0 10], в строке Y-axis range набрать [0 10] (рис. 1.4).
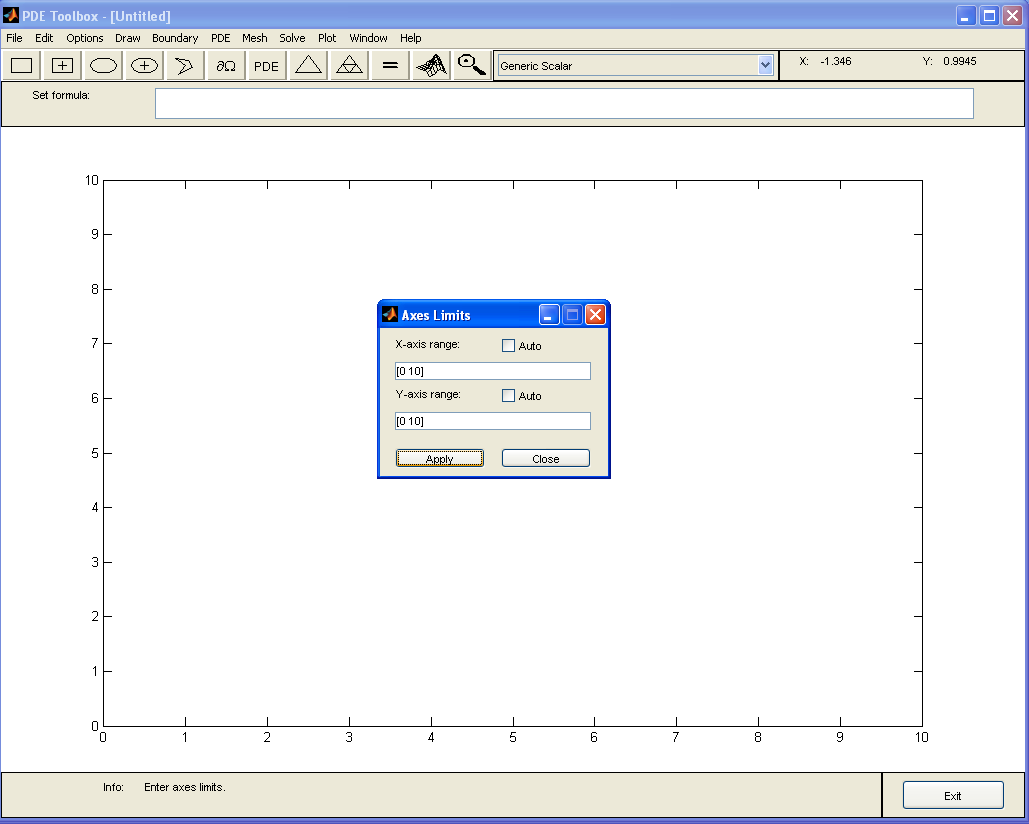
Рисунок 1.4 – Область задачи
При помощи панели инструментов нужно нарисовать канал. Сначала рисуем эллипс с центром в точке (0,0) и полуосями 5 и 5. Для уточнения координат дважды щелкаем по эллипсу. В окне Object Dialog устанавливаем параметры (рис. 1.5):
X-center 5
Y-center 5
A-semiaxes 5
B-semiaxes 5.
Аналогично рисуем второй эллипс с центром в точке (7,3) и полуосями 1 и 1, и прямоугольник длины 10 и ширины 1. В строке Set formula набираем: E1-E2-R1 (рис. 1.6).
Если держать Ctrl, то нарисуется сразу круг, что нам и надо!
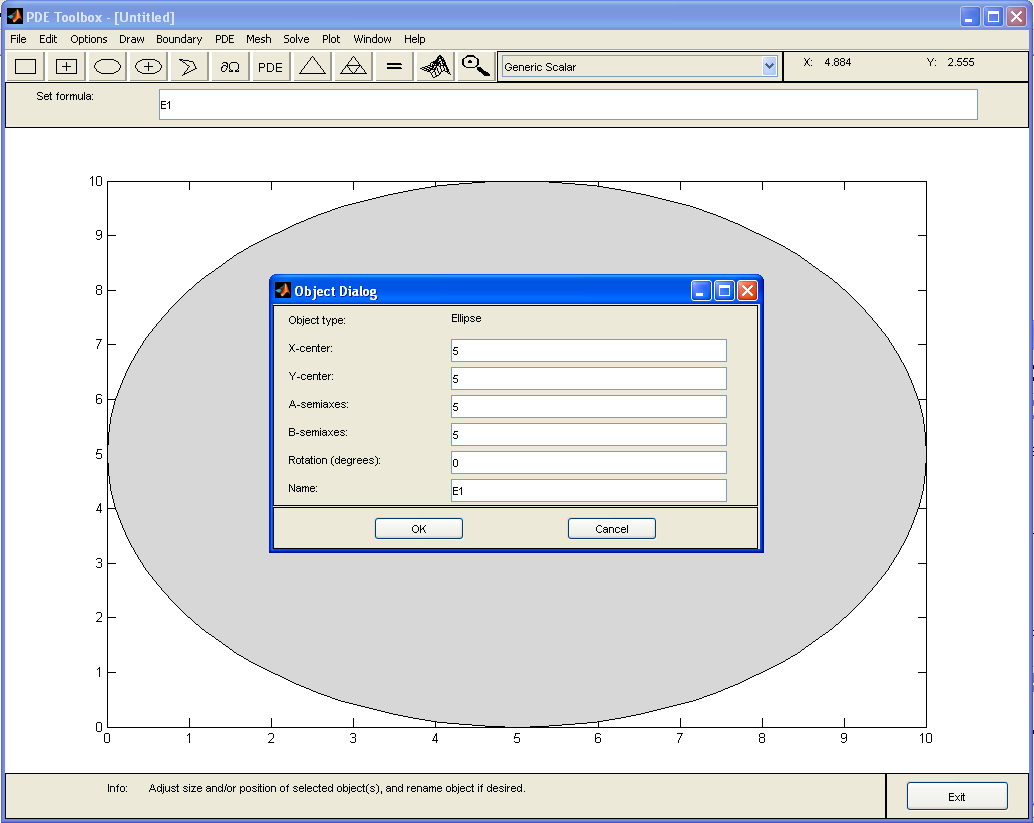
Рисунок 1.5 – Параметры объекта
Команды для редактирования изображения и настройки графического окна содержатся в следующих пунктах главного меню.
Edit (Правка) содержит команды:
Undo – отмена последнего действия;
Cut – вырезать выделенный геометрический объект и поместить его в буфер;
Copy – копировать выделенный объект в буфер;
Paste – вставить геометрический объект из буфера;
Clear – удалить выделенный объект;
Select All – выделить все геометрические объекты.
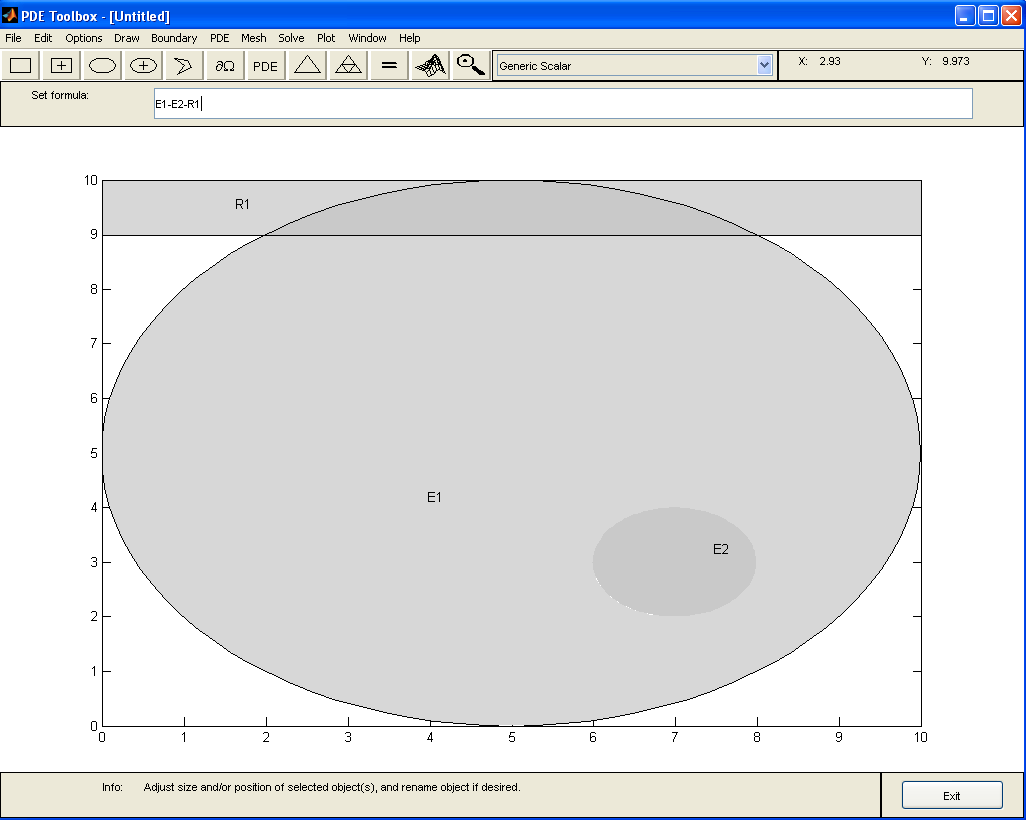
Рисунок 1.6 – Призматический канал
Options (Опции) содержит команды:
Grid – показать / скрыть координатную сетку;
Grid Spacing – установить пределы и шаг сетки;
Snap – округлять координаты указателя мыши;
Axes Limits – установить пределы координатных осей;
Axes Equal – установить одинаковый масштаб по осям x и y;
Zoom – показать с увеличением выделенную часть модели;
Application – переключение вида задачи;
Refresh – обновить изображение модели.
В т о р о й э т а п включает ввод граничных условий на граничных сегментах и параметров уравнения. Определить условие на любом из сегментов можно, выделив его двойным щелчком левой кнопки мыши. Соответствующие команды располагаются в разделах Boundary и PDE главного меню.
Boundary (Границы) содержит команды:
Boundary Mode – ввод граничных условий;
Specify Boundary Conditions… – ввод параметров граничных условий; Show Edge Labels – показать номера граничных сегментов;
Show Subdomain Labels – показать номера зон;
Remove Subdomain Border – удалить границу зон;
Remove All Subdomain Borders – удаление всех границ зон;
PDE (Уравнение) содержит команды:
PDE Mode – переключение в режим ввода параметров уравнения; Show Subdomain Labels – показать номера зон;
PDE Specification… – ввод параметров (коэффициентов) уравнения;
Export PDE Coefficients… – экспорт в базовую рабочую область переменных, описывающих PDE коэффициенты в расчётной области.
В
меню
Boundary
выберем
Boundary
Mode. Два
раза щелкаем по границе
,
в окне выбираем Dirihlet,
![]() (т.к.
(т.к.
![]() ).
Для данной задачи граница
будет состоять из четырех частей (рис.
1.7). Аналогично для границы
).
Для данной задачи граница
будет состоять из четырех частей (рис.
1.7). Аналогично для границы
![]() .
На границе
.
На границе
![]() выбираем Neumann,
выбираем Neumann,
![]() .
.
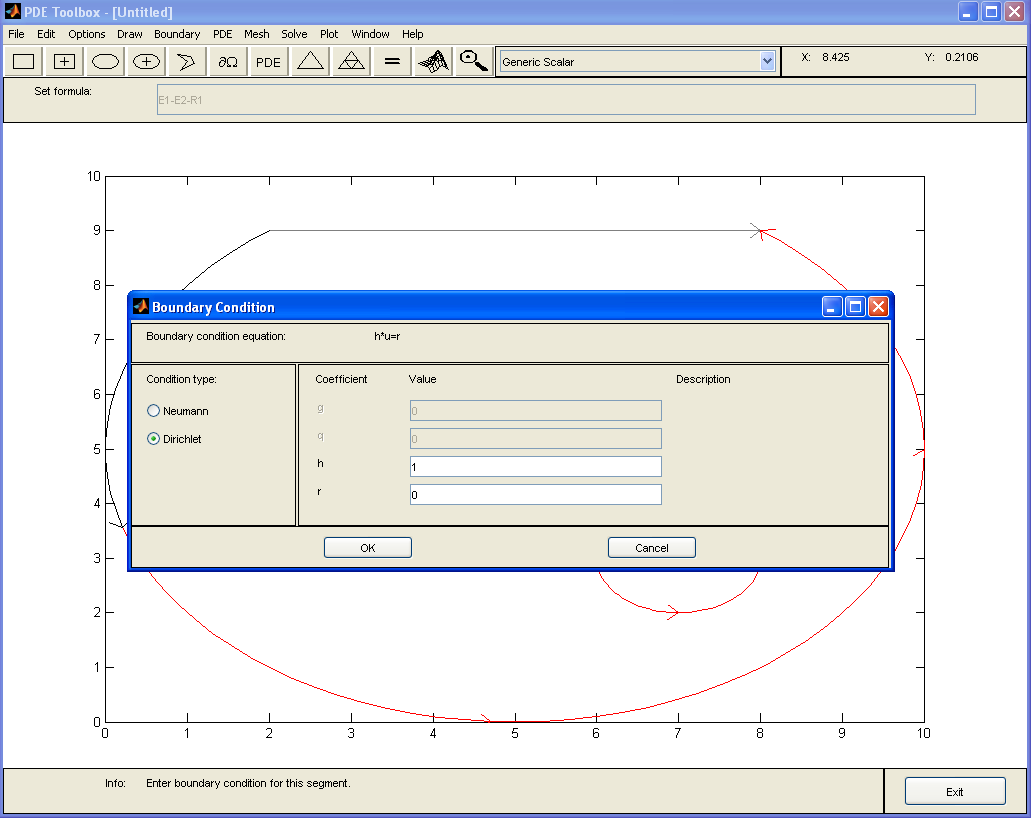
Рисунок 1.7 – Граничные условия
Зададим
параметры уравнения эллиптического
типа, вызвав через меню или панель
инструментов диалоговое окно "PDE
Specification". Выберем тип уравнения –
"Elliptic". Зададим
![]() (рис. 1.8).
(рис. 1.8).
Если в списке "Application" установлен режим "Electrostatics" (задача электростатическая), то в окне MATLAB уравнение имеет вид
–div(ε×grad(ϕ))=ρ,
где ε − диэлектрическая проницаемость, ϕ − электрический потенциал, ρ − объемный заряд.
В том случае, когда установлен режим "Generic Scalar" в списке "Application" (задача в обобщенной скалярной форме), запись уравнения в MATLAB имеет вид
–div(c×grad(u))+a×u=f
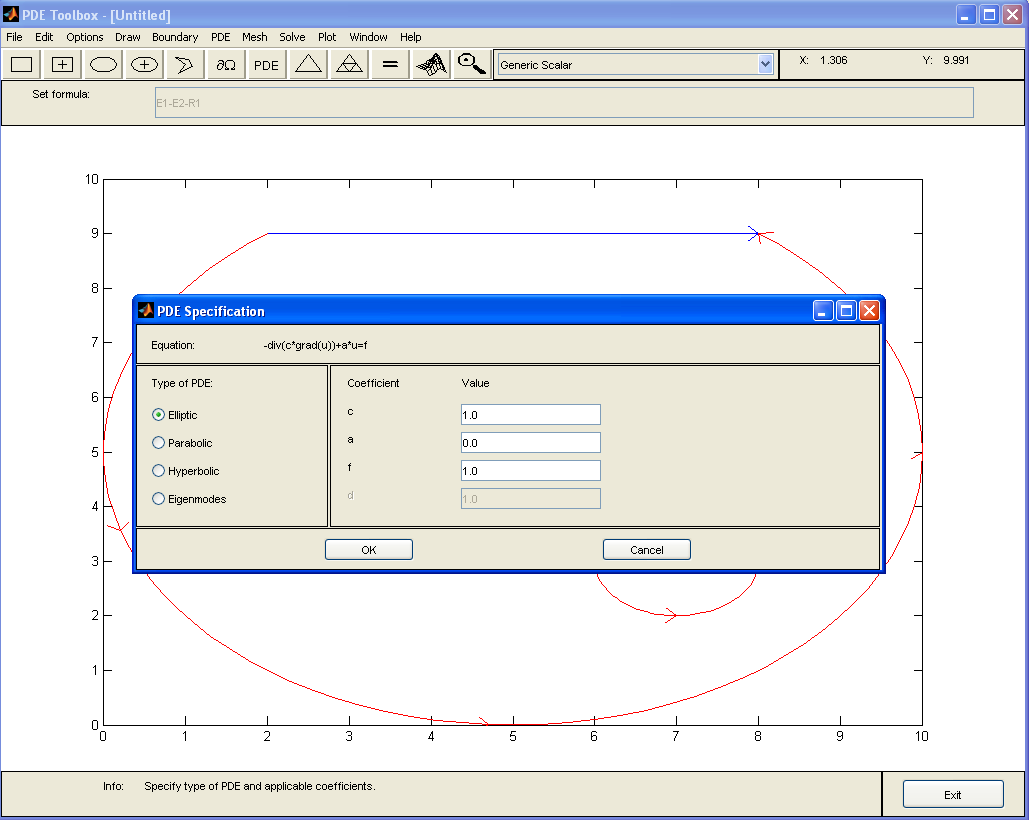
Рисунок 1.8 – Параметры уравнения
Н а с л е д у ю щ е м э т а п е формируется сетка конечных элементов (рис. 1.8). PDE Toolbox поддерживает только симплекс-элементы, для которых характерны линейные функции формы.
Пункт Mesh (Сетка) главного меню включает следующие команды для работы с сеткой:
Mesh Mode – переключение в режим построения сетки;
Initialize Mesh – генерация сетки; Refine Mesh – сгущение сетки;
Jiggle Mesh – регуляризация сетки в пределах установленной величины;
Undo Mesh Change – отменить последнее изменение сетки;
Display Triangle Quality – отобразить в цвете показатель регулярности конечных элементов;
Show Node Labels – показать номера узлов;
Show Triangle Labels – показать номера конечных элементов; Parameters… – установить параметры генератора сетки;
Export Mesh – экспорт сетки в базовую рабочую область.
С л е д у ю щ и й э т а п включает собственно решение задачи и его вывод в графическом виде (рис. 1.9). Соответствующие команды располагаются в пунктах Solve и Plot главного меню.
Solve (Решение) содержит команды:
Solve PDE – решить краевую задачу;
Parameters… – установить параметры решателя;
Export Solution… – экспорт решения в базовую рабочую область.
Для получения изолиний в меню Plot выбираем Parameters… ,где выбираем Contour.
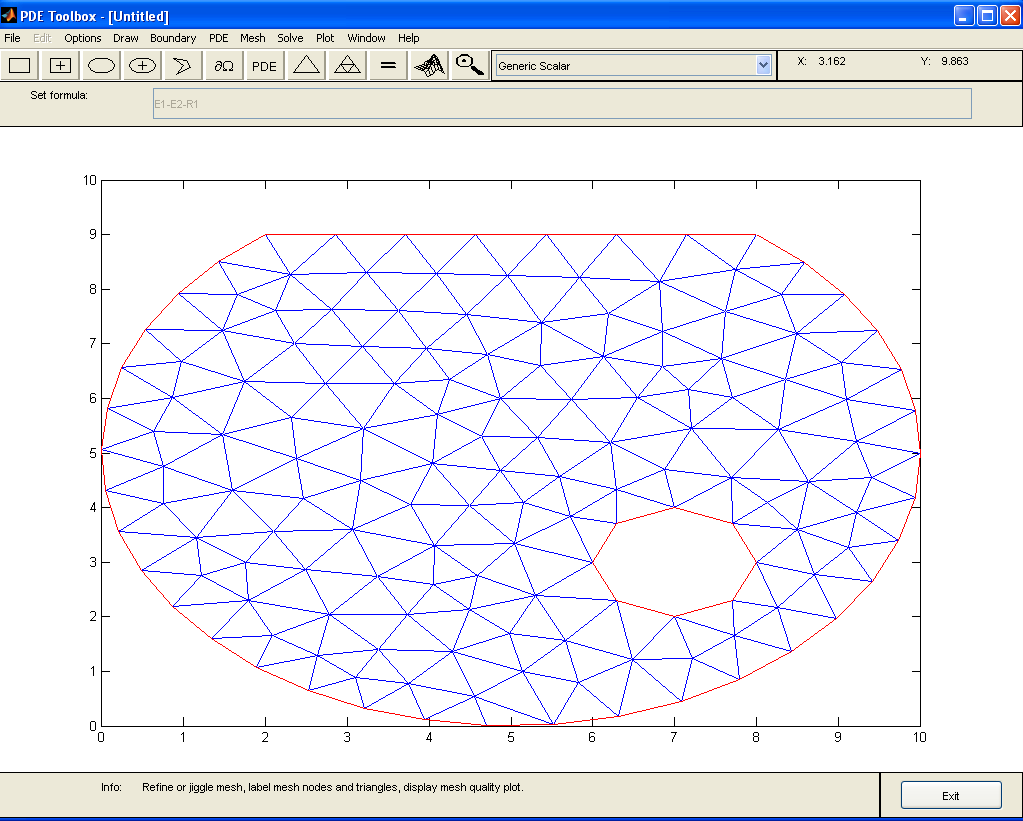
Рисунок 1.8 - Формирование сетки
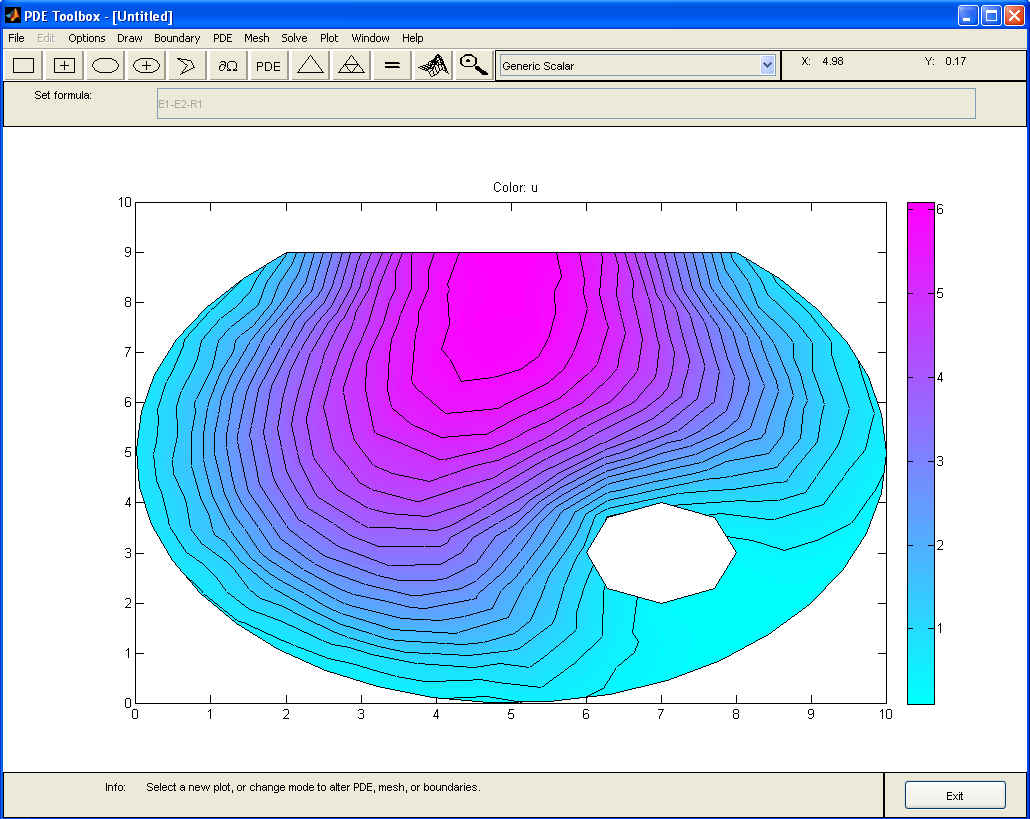
Рисунок 1.9 - Распределение эквипотенциальных линий
Результаты расчета можно сохранить, обратившись к пункту File (Файл) меню, включающему команды: New – создать новую модель; Open… – открыть ранее сохранённую в m-файле модель; Save – сохранение модели в m-файле с текущим именем; Save As… – сохранение модели в m-файле; Print… – печать рисунка.
