5.4 Загальні відомості про інтегральні рівняння Вольтерра

Визначення 3. Лінійним інтегральним рівнянням Вольтера називаються рівняння виду

(5.11)

(рівняння 2-го роду) або виду

(5.12)

(рівняння 1-го роду). В (5.11) і (5.12) – шукана функція, а ядро й вільний член передбачаються заданими відповідно в трикутнику , і на відрізку .

Розв'язком рівняння (5.11) будемо називати функцію , , що обертає це рівняння в тотожність. Будемо вважати, що функції й безперервні у своїй області визначення. При цій умові рівняння (5.11) має єдиний розв'язок у класі функцій, безперервних на .

5.5 Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра

Будується послідовність функцій , , де нульове наближення – довільна функція, а наступні наближення визначаються за допомогою рекурентного співвідношення:

, .

Якщо ядро й вільний член безперервні відповідно при , і на відрізку , то послідовність наближень , при сходиться до єдиного безперервного розв'язку інтегрального рівняння. Звичайно вважають .

Приклад 5.4. Методом послідовних наближень розв'язати рівняння .

Розв'язок. Прийнявши , послідовно знаходимо:

, .

У загальному випадку

.

Звідки .

5.6 Квадратурний метод розв'язку інтегральних рівнянь Вольтерра

Тому що лінійні інтегральні рівняння Вольтера мають єдиний безперервний розв'язок при будь-яких значеннях параметра , при знаходженні чисельного розв'язку рівняння Вольтерра другого роду можна покласти .

Враховуючи, що рівняння Вольтера можна вважати рівнянням Фредгольма: ,

с ядром . (5.13)

Для знаходження розв'язку розглянутого рівняння скористаємося результатами підрозділу 5.3.

Введемо в розгляд часову сітку , що складається з вузлів, і виберемо конкретну квадратурну формулу з вагами , тоді наближений розв'язок інтегрального рівняння має вид (7.9). Складемо СЛАУ, аналогічну системі (7.10), яка в силу властивостей ядра інтегрального рівняння (7.13) вироджується в трикутну:

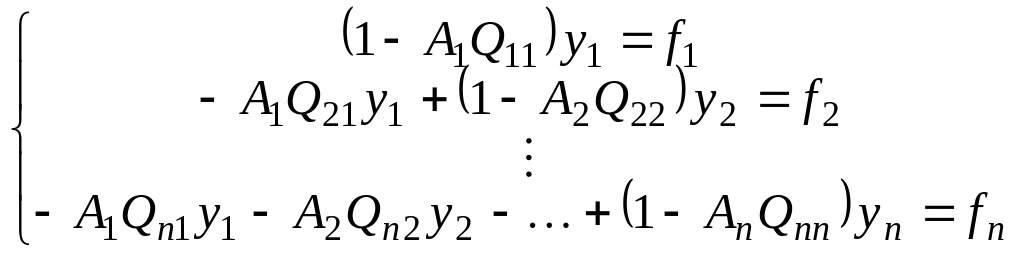(5.14)

З (5.14) видно, що невідомі значення знаходяться послідовними обчисленнями по формулах:

, , .

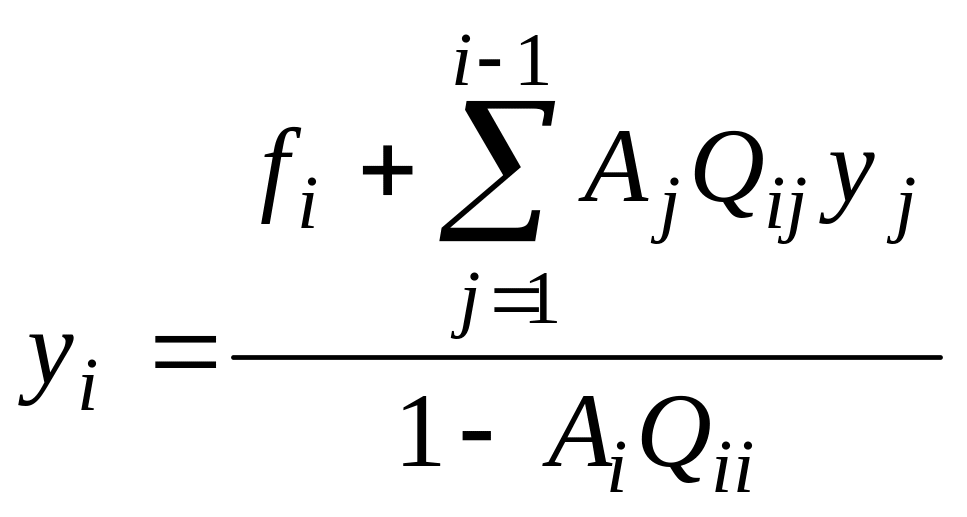Приклад 5.2. Інтегральне рівняння

Має точний розв'язок .

Знайдемо чисельний розв'язок цього рівняння, використовуючи метод трапецій, і порівняємо його з точним.

a=0; b=2.5; h=0.05; n=(b-a)/h+1; x(1)=a; y(1)=f(a);

for i=2:n

x(i)=a+(i-1)*h;

g=f(x(i));

for j=1:i-1

if (j==1) c=0.5; else c=1; end;

g=g+h*c*K(x(i),x(j))*y(j);

end;

y(i)=g/(1-h/2*K(x(i),x(i)));

ty(i)=exp(x(i))*(cos(exp(x(i)))-p(x(i))*sin(exp(x(i))));

end; plot(x,y,x,ty,'.'); grid on;

Функції:

function y=f(x)

y=(1-x*exp(2*x))*cos(1)-exp(2*x)*sin(1);

function z=K(x,t)

z=1-(x-t)*exp(2*x);

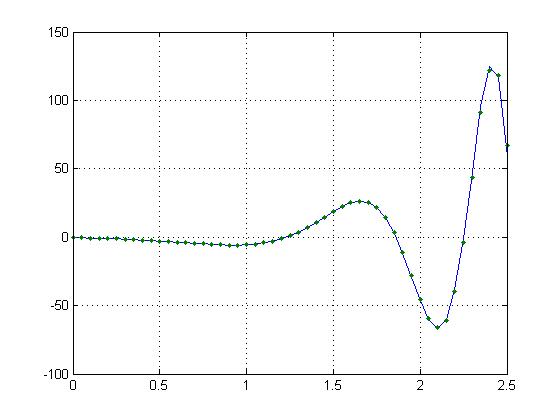
Рисунок 5.1 – Точний й наближений розв'язок прикладу 5.2.