Средние время по перебору ключей

Длина ключа(бит)	Количество различный ключей	Необходимое время при скорости 1 шифрование в 1 мс.	Необходимое время в 106 шиф\мс
32	232	231 мс=35,8 мин	2,15 мс
56	256	255мс=1142 года	10,01 часа
128	2128	2127мс=5,4*1024лет	5,4*1018лет
26	26!	6,4*1012лет	6,4*106лет

Пусть некоторый алфавит Z, в известном случае его можно приставить в = {a₀,a₂,…a_m-1}, можно создать новый алфавит = {a₀₀,a₀₁,…a_m-1m-1} и т.д. Используя алфавит ис небольшим количеством , так его можно усложнить . замена букв алфавит позволяет сформулировать основные концепции. В шифрах перестановки могут использоваться шифрующие таблицы. В качестве ключа шифруемых таблицах могу использоваться размер таблицы, слово или фраза задающие перестановку.

Особенности структуры таблицы.

Лекция 9

Основная схема симметричного кодирования

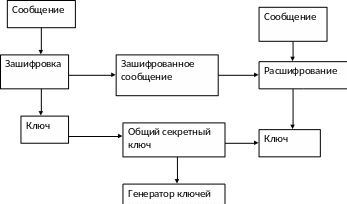
Достоинтсво – ключ один. Основной недостаток – ключ должен быть известен и отправителю и получателю сообщений. С одной стороны такой факт создает новую проблему распространения ключей, а с другой получатель даже на основании наличия у него зашифрованного и расшифрованного текста сообщений не может доказать что он получи это сообщение от конкретного отправителя. Так как то же сообщение он мог сгенерировать самостоятельно.

Доказуемость переданного сообщения, невозможность отказа, для устранения этих 2 недостатков были предложены ассиметричные системы шифрования. В них используются 2 ключа – 1 из них не секретный применяется для шифрования, а второй секретный известный только получатель применяется для расшифрования. Не секретный ключ может публиковаться вместе с другими не секретными(открытыми) сведениями о пользователе.

Системы с открытым ключом – ассиметричные системы

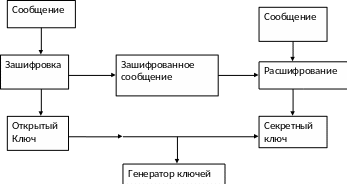
Эту концепцию предложили в 70х годах Диффи и Хелмен, поэтому он иногда называется методом Диффи-Хелмена. Эта концепция заключается в том что один ключ из другого получить не возможно, и используется 2 ключа, 1 открытый и 1 закрытый.

Самый популярный из ассиметричных методов – метод, разработанный Rivest, Shamir, Adleman – метод RSA. Он основан на операциях с большими простыми числами и их произведении.

Метод RSA

Исходный текст должен быть переведен в числовую форму. Метод преобразования текста в числовую форму считается известным и не обязательно держать его в секрете. В результате такого преобразования текста представляется в виде одного большого числа. Затем это полученное число разбивается на части так, что бы каждая из этих частей была в промежутке [0,N]. Процесс шифрования одинаков для каждой части, поэтому считают что исходный текст представлен некоторым числом 0<x<N. Пусть некоторый пользователь желает, что бы ему передали секретное сообщение, для этого он делает общедоступными 2 числа N,e. Эти числа подчинены 2 условиям:

1. N=p*q p и q – большие простые числа который пользователь держит в секрете. Обычно они выбираются порядком не ниже чем 2²⁵⁶

2. фи(N)=(p-1)(q-1)

Второй пользователь отправляя некоторое сообщение Х шифрует его так

y=E(x)=x^e(mod N) В результате получается зашифрованный текст который отправляется пользователю 1.

Для восстановления исходного текста получатель поступает так:

1. находит некоторое число d которое удовлетворяет условиям 1<=d<=N-1,

ed=*тождественно равно*1(mod фи(N)). Это сравнение разрешимо единственным образом так как (e,фи(N))=1 общий множитель у этих чисел всего один. Для получения d получатель должен вычислить значение фи(N).

Любой другой пользователь который знает только значение N должен находить значения p,q тоесть разлагать N на большие сомножители. При больших p,q эта задача имеет большую выслительную сложность.

2. Имея в распоряжении число y, получатель вычисляет некоторое преобразование D(y)=y^d(mod N) а оно и дает представление значение исходного текста х.

y^d= x^ed= x^фи(N)k+1(x^фи(N))^kx=x(mod N) *все равно – тождественно равно* теорема Эйлера

(e,фи(N))=1

Замечание: x^p-1=1(mod p) x^q-1=1(mod q) тогда если положить l=фи(N)=(p-1)(q-1)

X^l=1(mod p) x^l=1(mod q)  x^l=1(mod фи(N))

Из этого следует что для любых e’и d’ с условиями e’=e(mod l) d’=(mod l) e’и d’ будут такими же соответственно открытым и секретным ключом.

…

Для обеспечения стойкости предьявляют целый набор требований к параметрам.

E(x1 x2)=E(x1)E(x2)

Формулы(!)

Два преобразования E и D являются взаимообратными, что обеспечивается условием

Это значит, что секретный и открытый ключи можно менять местами.

Требования к выбору параметров в системе RSA:

1. простые числа p и q должны быть большими

2. разность их также должна быть большой (p-q) по модулю

3. числа p+-1 и q+-1 должны содержать большой просто множитель

4. общий делитель этих чисел должен быть не большим (p-1,q-1)

5. нельзя выбирать ключи e,d с короткой секретной экспонентой [p-1,q-1]

Безопасность метода RSA

Она зависит от проблемы разложения больших чисел на множители.

Математически никогда не доказывалось что нужно разложить N на множители что бы восстановить сообщение х по величине у и ключу е. Для криптоанализа может быть применен совсем другой способ, и если он позволит получить ключ D его также можно применить для разложения больших чисел на множители.

Шифр RSA можно также вскрыть угадав значения произведения (p-1*q-1)

Имеется еше одно беспокойство, большинство общепринятых алгоритмов вычисления больших чисел носят вероятностный характер.

…

Существенным недостатком ассиметричных методов шифрования является их сложность а, следовательно, низкое быстродействие. Поэтому такие методы, основанные на RSA, используются в сочетании с симметричными.

Ассиметричные методы работают на 3 а иногда и 4 порядка медленнее чем симметричные. Как при шифровании, так и при расшифровании алгоритм RSA по существу состоит из операций возведения в степень, которые выполняются как последовательный ряд умножений. В практических приложениях для открытого ключа обычно выбирается относительно не большой показатель, и часто целые группы пользователей имеют один и тот же показатель но каждый с различным модулем. Если открытый показатель неизменен то вводятся некоторые ограничения на главные делители модуля (факторы). При этом шифрование данных происходит быстрее, чем расшифрование. Если в шифруемом модуле k бит, то алгоритм RSA количество шагов необходимых для операций с открытым ключом пропорционально k². Количество шагов для операций закрытого ключа пропорционально k³, а … k⁴

Методы быстрого умножения например быстрое преобразование Фурье выполняются меньшим количеством шагов, но …

Алгоритм RSA намного медленнее чем алгоритм Des и другие алгоритмы блочного шифрования. …

Возможные атаки на систему RSA

Набор (N=p*q, e, d) параметров задают криптоситему RSA. Для ее взлома необходимо по известным входным величинам N,e и зашифрованному сообщению? Необходимо найти также значения xЄ(Z/(N)) y=x^e(mod N) Наиболее распространен метод атаки под названием метод повторного шифрования.

Лекция №10

Вычисление ключей

Выбор p,q . Они должны быть простыми

Вычисление n=p*q

Вычисление

Выбор целого е ,

Вычисление

Открытый ключ

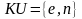
Личный ключ

Пример:

1. выберем два простых числа p=7, q=17

2. N=p*q=119

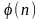3. =(7-1)*(17-1)=6*16=96

4. е=5

5. d: d*e=1mod96, d:

77*5=385=4*96+1

d=77

Пусть в качестве ОТ поступает число 19.

19⁵ mod119 = 66 (19->19⁵=2476099/119=66 (остаток от деления 66))

Если без искажения передаётся, то тогда нужно провести восстановление

ШТ : 66

Ключ = 77

66⁷⁷(mod 119) = 19 – открытый текст (ОТ)

Сравнительная характеристика методов традиционного шифрования

и шифрования с открытым ключом

№	Традиционные	Открытый ключ
Необходимое для работы
1	Один алгоритм с одним и тем же ключом служит и для шифрования и для расшифрования	И для шифрования и расшифрования используется одинаковый алгоритм, но 2 ключа
2	Отправитель и получатель сообщения должны использовать одинаковые алгоритм и ключ	Отправитель и получатель должны иметь по одному из пары соответствующих друг другу ключей
Необходимое для защиты
1	Ключ должен сохраняться в секрете	Один из двух ключей должен сохраняться в секрете
2	Должно быть невозможно или, по крайней мере, практически невозможно расшифровать сообщение при отсутствии дополнительной информации
3	Знание алгоритма и наличие образцов шифрованного текста должно быть недостаточно для того, чтобы восстановить ключ	Знание алгоритма и одного из ключей, а также наличие образцов шифрованного текста должно быть недостаточно для того, чтобы восстановить второй ключ

При вычислении сложности реализации алгоритма RSA обращают внимание на 2 вопроса:

- сложность шифрования/дешифрования

- сложность вычисления ключей при этом

И при шифровании и при дешифровании используется возведение целого числа в степень и сравнение по модулю. Если возведение в степень выполнять непосредственно с целыми числами, а затем проводить сравнение по модулю N, то промежуточные при этих операциях значения могут оказаться огромными величинами.

1. Для того чтобы немного упростить и понизить размерность величин полезно использовать такие соотношения:

Эта запись позволяет промежуточные вычисления уже брать по модулю N. в этом случае вычисления становятся практически реализуемые.

2. Эффективная реализация операции возведения в степень.

Х¹⁶ = х² -> x⁴ -> x⁸ -> x¹⁶

Сгруппировав данные можно сократить количество операций:

Пусть нужно найти a^m, где a и m – положительные целые числа. Число m представим в виде двоичной последовательности bтит-1…и1и0

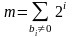
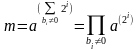
3. Вычисление ключей

Прежде чем использовать систему с открытым ключом у каждой из сторон должна быть возможность сгенерировать пару ключей. А это значит выполнение следующих действий:

1 – Определение простых чисел p и q

2 – Выбор одного из чисел e или d, и вычисление другого

Если это возможно сделать и отправителю и получателю, то можно задействовать систему с открытым ключом. Так как n=p*q, то чтобы не позволить противнику определить p и q с помощью простого перебора, эти простые числа должны быть выбраны из достаточно большого множества.

Метод нахождения больших простых чисел должен быть практически эффективным.

В настоящее время нет хороших методов вычисления произвольно больших простых чисел, и для их определения прибегают к различным хитростям. Чаще всего процедура заключается в выборе случайного нечётного числа приблизительно желаемой величины и выяснения является ли это число простым. Если окажется, что оно не является простым, то выбирается другое число и т.д. для проверки того, что числа простые существует следующий ряд тестов. Почти все они носят вероятностный характер. Такой тест определит только то, что конкретное число вероятно является простым. Несмотря на отсутствие полной уверенности, что результатами теста обеспечивается достоверность или вероятность того, что это число является простым, близится к 1.

Одним из наиболее популярных и эффективных алгоритмов является алгоритм Миллера-Рабина. Проверка простоты конкретного целого числа N заключается в выполнении ряда вычислений, в которых используется число N и некоторое случайно выбранное целое число А. Если оно не выдерживает тестирование, то оно и не является простым. Если же N выдерживает одно тестирование, то оно может оказаться простым, а может и нет. Если значение N успешно проходит целый ряд испытаний с различными случайными А, то это даёт нам большую уверенность, что число N является простым.

Процедура выбора простого числа:

1. Выбрать нечётное целое число некоторым случайным образом.

2. Выбирается целое число А, меньшее чем N случайным образом

3. Выполняется вероятностный тест на простоту (например, Миллера-Рабина). Если число N не проходит тестирование, то оно отбрасывается и возвращаемся к пункту 1.

4. Если N проходит испытание, то возвращаемся к пункту 2. Если же число N выдерживает ряд испытаний, то оно подходит на роль целого и простого.