2.2 Способы задания бинарных отношений

Пусть для aA и bB задано отношение RAB и оно определено в соответствии с рисунком.

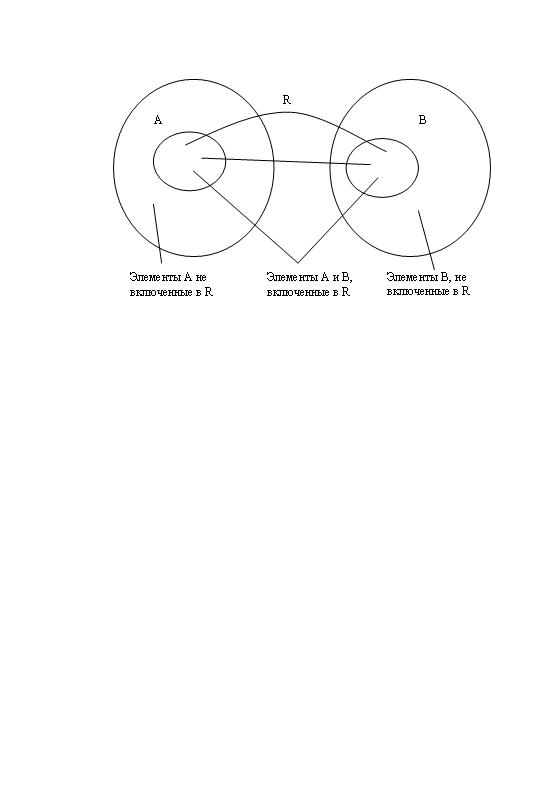
Рисунок 5. Отношение.

Область определения D(R) и область значений E(R) определяются соответственно:

D(R)={a  (a,b)  R}

E(R)={b  (a,b)  R}

Отношения, определенные на конечных множествах, обычно задаются:

1. Cписком (перечислением) пар, для которых это отношение выполняется. Например, R={(a,b),(a,c),(b,d)}, англо-русский словарь.

2. Матрицей (соответствия). Бинарному отношению RMM, где M={a₁ ,a₂ ,a₃ … a_n}, соответствует квадратная матрица n, в которой элемент c_i,j равен 1, если между a_i и a_j имеет место отношение R, или 0, если оно отсутствует.

Пример 1. Пусть М={1,2,3,4,5,6}. Задать списком и матрицей соответствие отношений RMxM, если R-«строго меньше».

Задать матрицей соответствия отношения на множестве M:

R₁-«быть делителем»

R₂-«иметь общий делитель, отличный от 1»

R₃-«иметь один и тот же остаток деление на 3»

Решение: отношение R как множество содержит все пары элементов a, b из M такие, что a<b:

R={(1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (3,7), (4,5), (4,6), (5,6)}

Матрица отношения R – “быть строго меньше” выглядит следующим образом.

R	1	2	3	4	5	6
1	0	1	1	1	1	1
2	0	0	1	1	1	1
3	0	0	0	1	1	1
4	0	0	0	0	1	1
5	0	0	0	0	0	1
6	0	0	0	0	0	0

Матрица отношения R₁ – «быть делителем»

R1	1	2	3	4	5	6
1	1	1	1	1	1	1
2	0	1	0	1	0	1
3	0	0	1	0	0	1
4	0	0	0	1	0	0
5	0	0	0	0	1	0
6	0	0	0	0	0	1

Матрица отношения R₂ – «иметь общий делитель отличный от 1»

R2	1	2	3	4	5	6
1	0	0	0	0	0	0
2	0	1	0	1	0	1
3	0	0	1	0	0	1
4	0	1	0	1	0	1
5	0	0	0	0	1	0
6	0	1	1	1	0	1

Матрица отношения R₃ – «иметь один и тот же остаток от деления на 3»

R3	1	2	3	4	5	6
1	1	0	0	1	0	0
2	0	1	0	0	1	0
3	0	0	1	0	0	1
4	1	0	0	1	0	0
5	0	1	0	0	1	0
6	0	0	1	0	0	1