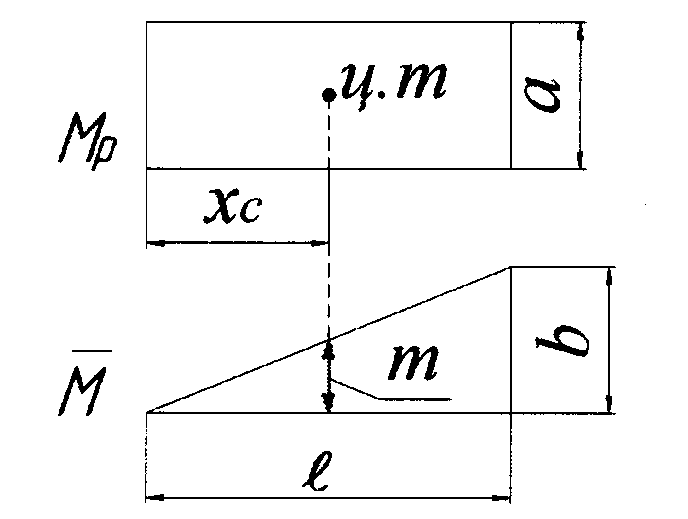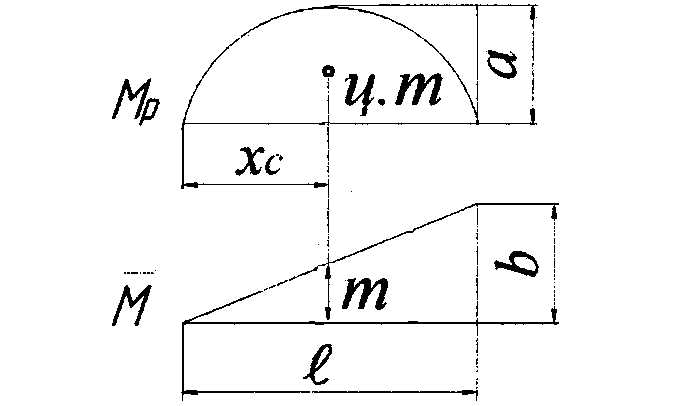2. Правило Мора-Верещагина (графический способ вычисления
интеграла Мора)
Кроме
метода начальных параметров существует
эффективный универсальный метод
определения перемещений в балках, рамах
и упругих конструкциях произвольной
конфигурации – метод Мора. Упругое
перемещение
(либо прогиб
,
либо угол поворота сечения
)
определяется по формуле:
,
(1.3)
где
– изгибающий момент от заданной нагрузки;
– изгибающий момент от единичной силы,
приложенной в той точке, в которой
определяется перемещение.
Упрощение
операций интегрирования возможно для
конструкций с прямолинейной осью
постоянной жесткости и основано на том,
что эпюры от единичных усилий на
прямолинейных участках оказываются
линейными. Рассматривая эту процедуру
применительно к участку балки, преобразуем
интеграл Мора с учетом этой особенности.
На рис. 1.3 сверху показан участок балки
с эпюрой
общего вида, а внизу эпюра
,
представляющая собой линейную функцию.
В результате несложного расчета
(подробности смотри в учебнике)
установлено, что интеграл произведения
двух функций
и
численно равен площади эпюры
,
умноженной на величину момента, взятого
с эпюры
в сечении, соответствующем центру
тяжести эпюры
.
.
(1.4)
– обобщённое
перемещение: либо прогиб
,
либо угол поворота
.
Если вычисляем прогиб, то в этой точке
по направлению искомого прогиба к
ненагруженной балке прикладываем
единичную силу
и строим эпюру
.
Если вычисляем угол поворота
,
то к ненагруженной балке в этой точке
по направлению искомого углового
перемещения прикладываем единичный
момент
и строим эпюру
.
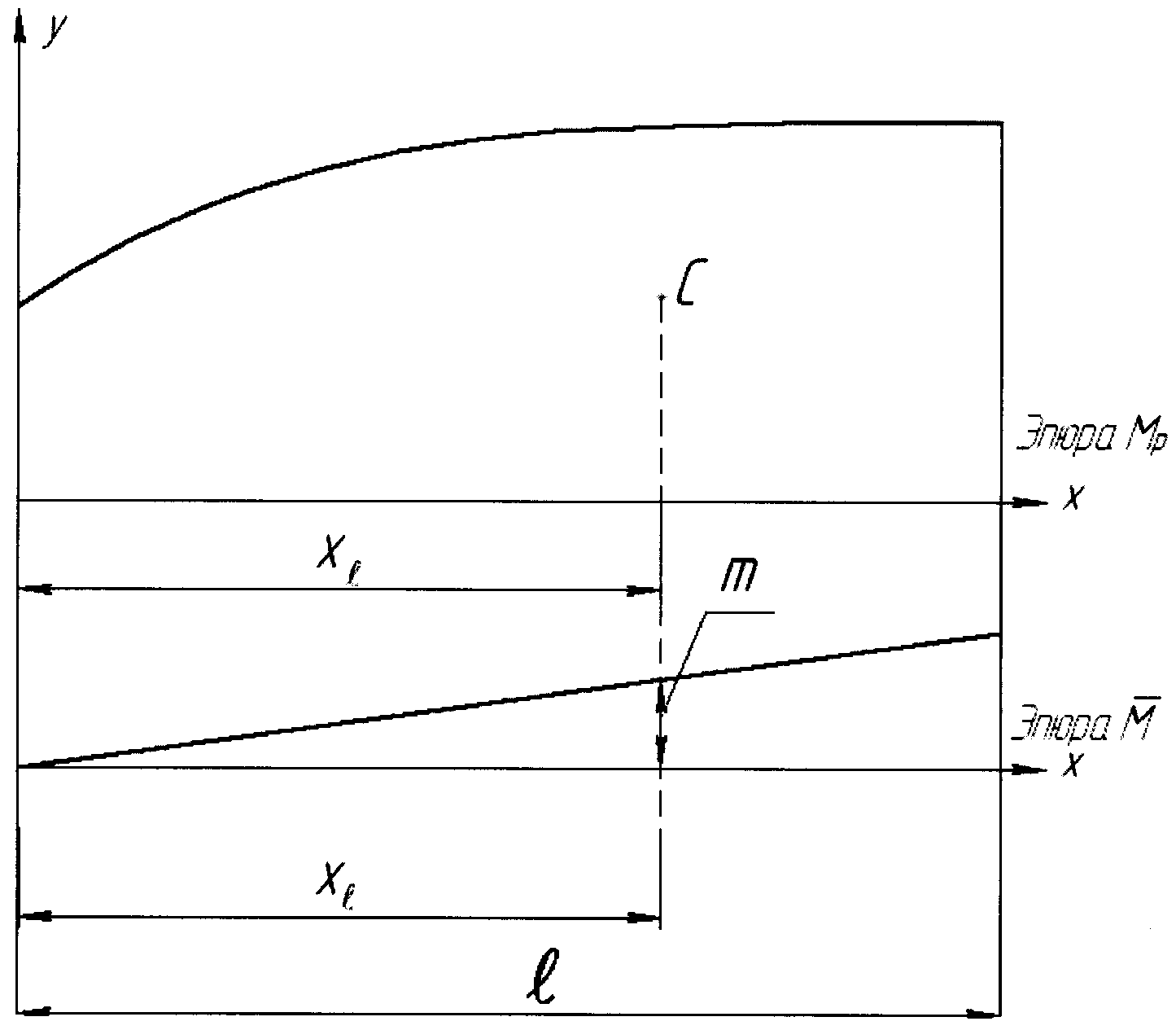
Рис. 1.3.
Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид
,
(1.5)
где
– площадь эпюры моментов от внешней
нагрузки (грузовой эпюры);
– ордината единичной эпюры под центром
тяжести грузовой эпюры;
– число участков по длине балки.
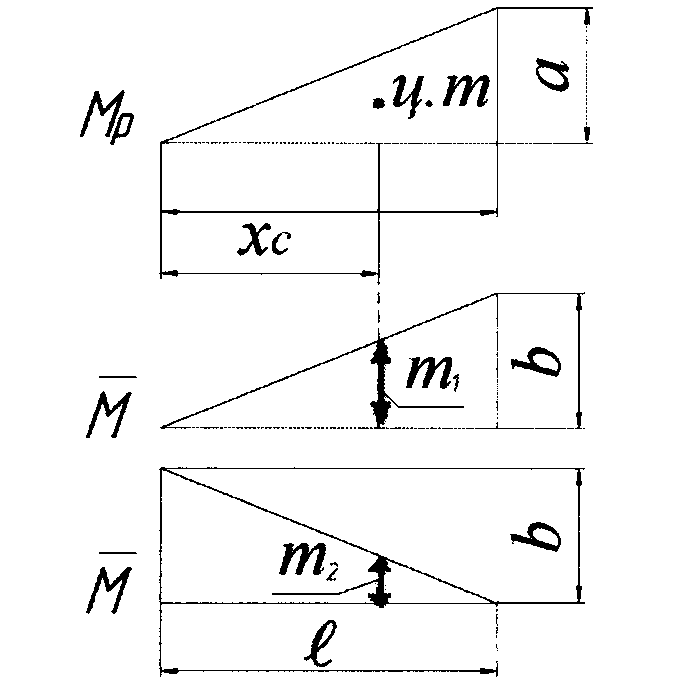
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.
Таблица 1.1
Эпюры и |
Площадь грузовой опоры |
Ордината единичной
эпюры
координата центра
тяжести
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
,
Окончание табл. 1.1
Эпюры и |
Площадь грузовой опоры |
Ордината единичной эпюры , координата центра тяжести |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
П р и м е ч а н и я: 1. Все кривые в табл. 1.1 – квадратные параболы; 2. При «перемножении» эпюр одного знака их произведение положительно; 3. При «перемножении» эпюр разных знаков их произведение отрицательно.
В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
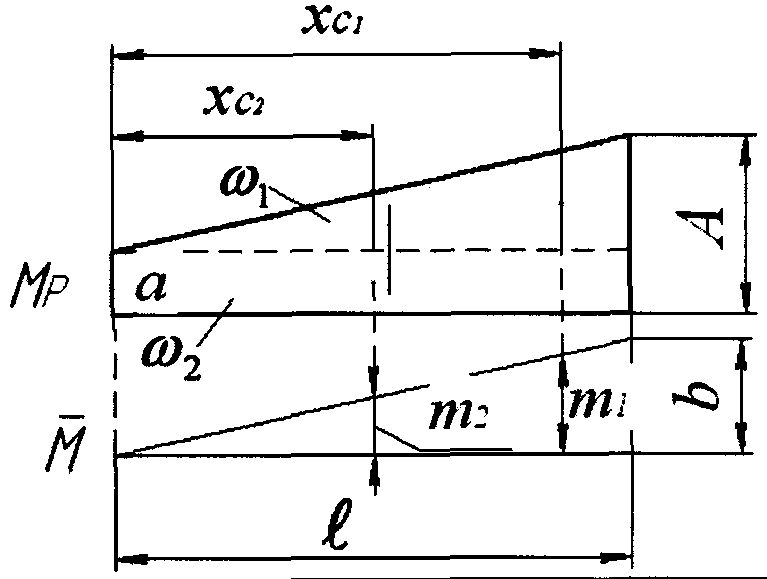
Рассмотрим
на примере расчетной схемы, показанной
на рис. 1.4, порядок решения задач при
определении перемещения с помощью
правила Мора-Верещагина. Определим
прогиб в точке
.
Чтобы
построить эпюры
и
,
можно не определять опорные реакции:
достаточно сосчитать момент на опоре
от нагрузки на консоли, построить эпюру
на консоли, а затем соединить прямой
линией значение M
на опоре B с
нулем на опоре A.
В соответствии с формулой (1.5)
.
Знак «+» означает, что перемещение происходит в направлении единичной силы.
Рис. 1.4.