3.6. Визначення взаємозв’язків між факторними та результативними ознаками

Існують такі види зв’язку:

• функціональний – кожному значенню факторної ознаки відповідає одне значення результативної.

• стохастичний - кожному значенню факторної ознаки відповідає множина значень результативної, які утворюють умовний розподіл.

В даній частині курсової роботи буде виявлений зв’язок між продуктивністю праці та часом у русі, оскільки це основні показники, які характеризують виконання плану.

Існує декілька методів виявлення зв’язка між двома ознаками:

• метод аналітичних групувань;

• метод регресії і кореляції;

• кореляції рангів.

В даній частині курсової роботи буде виявлений зв’язок між продуктивністю праці та часом у русі за допомогою метода аналітичних групувань та метода регресії та кореляції.

Вимірювання зв’язку методом аналітичних групувань, який складається з 2 етапів:

1. побудова аналітичного групування;

2. визначення щільності зв’язку між факторною та результативною ознакою за формулою:

,

де -міжгрупова дисперсія,

- загальна дисперсія.

Використаємо аналітичне групування за часом у русі, що приведене в таблиці №11 розділу 2.

Для того, щоб обчислити загальну дисперсію побудуємо

таблицю №17 розподілу продуктивності праці, яку виконав кожен водій за 6 днів роботи:

Зведення по продуктивності праці за 6 днів роботи

Таблиця №17

№	Y- Продуктивність праці	Y2
1	125	15625
2	132	17424
3	131	17161
4	141	19881
5	136	18496
6	130	16900
7	147	21609
8	126	15876
9	136	18496
10	136	18496
11	129	16641
12	132	17424
13	129	16641
14	138	19044
15	141	19881
16	124	15376
17	133	17689
18	129	16641
19	141	19881
20	147	21609
21	153	23409
22	137	18769
23	138	19044
24	127	16129
25	121	14641
26	134	17956
27	131	17161
28	138	19044
∑	3762	506944

Знайдемо значення загальної дисперсії:

= 506944/28 – (3762/28)²=18105,14 – 18063,36 = 41,78

Побудуємо таблицю для обчислення міжгрупової дисперсії:

Таблиця №18.

Розрахунок міжгалузевої дисперсії в аналітичному групуванні

№	Час у русі (год.)	Кількість водіїв	Середня продуктивність праці (т/год)
1	32 – 35,2	4	139,25	4,85	23,5	94
2	35,2 – 38,4	1	132	-2,4	5,76	5,76
3	38,4 – 41,6	7	136,14	1,74	3,03	21,21
4	41,6 – 44,8	9	133,7	-0,7	0,49	4,41
5	44,8 – 48	6	131	-3,4	11,56	69,36
6	48 - 51	1	131	-3,4	11,56	11,56
∑		28				206,3

Для обчислення між групової дисперсії використаємо формулу:

,

де - середнє значення ознаки (продуктивності праці) по всій сукупності;

= 134,4 (т/год)

- середнє значення ознаки для кожної з груп;

- частоти.

=206,3/28 = 7,4

Отже, обчислимо щільність зв’язку між часом у русі та продуктивністю праці:

= 7,4/ 41,78 = 0,2

Оскільки = 0,2 , то можна сказати, що зв’язок слабкий, тобто на 20% продуктивність праці залежить від часу у русі, а 80% - вплив інших факторів.

Цей метод дає добрі результати коли використовується велика кількість одиниць сукупності, а недолік – неможливо отримати теоретичну лінію регресії, яка характеризує стохастичний зв’язок.

Цей недолік враховує метод регресії та кореляції, тому визначимо зв’язок між часом у русі та продуктивністю праці за допомогою цього методу.

З адача метода регресії та кореляції полягає у виявленні зв’язку між факторною та результативною ознаками, та виборі рівняння регресії методом найменших квадратів. Це означає, що сума різниць квадратів теоретичних і емпіричних значень повинна бути мінімальною.

(У_і - У)² min

Необхідно знайти параметри рівняння: У = а + b*х

де а – параметр, що показує значення результативної ознаки (у), якщо факторна ознака х=0;

b – параметр, що показує на скільки одиниці змінюється середньому результативна ознака (у), якщо факторну ознаку змінити на одиницю.

Для находження параметрів будується система рівнянь:

na + b x =  y

a x + b x² =  xy

Для розв’язку системи рівнянь будується допоміжна таблиця.

Щ об виявити щільність зв’язку, вимірюють лінійний коефіцієнт кореляції R: R = ( X*Y – X*Y) / (_x*_y)

Лінійний коефіцієнт кореляції R змінюється в межах - 1  R  +1. Він показує напрямок і тісноту зв’язку між ознаками.

Отже, знайдемо взаємозв’язок між факторною ознакою – часом у русі (Х_і), та результативною ознакою – продуктивнітю праці ( У_і ), побудувавши допоміжну таблицю за допомогою зведення.

Таблиця №19

Взаємозв’язок між факторною ознакою – часом у русі ( Х_і ), та результативною ознакою – продуктивністю праці ( У_і )

№	Хі	Уі	Хі2	Хі * Уі	( Хі – Х)2	( Уі – У )2
1	43	125	1849	5375	1,69	88,36
2	39	132	1521	5148	7,29	5,76
3	51	131	2601	6681	86,49	11,56
4	35	141	1225	4935	44,89	43,56
5	43	136	1849	5848	1,69	2,56
6	41	130	1681	5330	0,49	19,36
7	42	147	1764	6174	0,09	158,76
8	47	126	2209	5922	28,09	70,56
9	47	136	2209	6392	28,09	2,56
10	40	136	1600	5440	2,89	2,56
11	42	129	1764	5419	0,09	29,16
12	38	132	1444	5016	13,69	5,76
13	46	129	2116	5934	18,49	29,16
14	43	138	1849	5934	1,69	12,96
15	43	141	1849	6063	1,69	43,56
16	44	124	1936	5456	5,29	108,16
17	40	133	1600	5320	2,89	1,96
18	43	129	1849	5547	1,69	29,16
19	33	141	1089	4653	75,69	43,56
20	46	147	2116	6762	18,49	158,76
21	39	153	1521	5967	7,29	345,96
22	34	137	1156	4658	59,29	6,76
23	39	138	1521	5382	7,29	12,96
24	48	127	2304	6096	39,69	54,76
25	46	121	2116	5566	18,49	179,56
26	43	134	1849	5762	1,69	0,16
27	39	131	1521	5109	7,29	11,56
28	32	138	1024	4416	94,09	12,96
	1166	3762	49132	156305	576,52	1492,48
Середні значення	41,7	134,4		5582,3

Припускаючи, що залежність лінійна, знаходимо коефіцієнти емпіричного рівняння:

У = а + b*x ,

У=160-0,6*х

Т аблиця №20

Розрахунок теоретичних значень У:

№	Хі	Уі	У
1	43	125	134,2
2	39	132	136,6
3	51	131	129,4
4	35	138	139
5	43	136	134,7
6	41	130	135,4
7	42	147	134,8
8	47	126	131,8
9	47	136	131,8
10	40	136	136
11	42	129	134,8
12	38	132	137,2
13	46	129	132,4
14	43	138	134,2
15	43	141	134,2
16	44	124	133,6
17	40	133	136
18	43	129	134,2
19	33	141	140,2
20	46	147	132,4
21	39	153	136,6
22	34	137	139,6
23	39	138	136,9
24	48	127	131,2
25	46	121	132,4
26	43	134	134,2
27	39	131	136,6
28	32	138	140,8
	1166	3759

За даними таблиці №19 знаходимо середньоквадратичні відхилення, щоб визначити тісноту зв’язку:

_х = (576,52/28)^1/2 = 4,5

_у = (1492,48/28)^1/2 = 7,3

R = (5582,3‑ 41,7*134,4) / (4,5 * 7,3) = -0,7

Оскільки коефіцієнт R близький до -1, то зв'язок між ознаками тісний, а знак « - » вказує на те, що зв'язок обернений.

Отже взаємозв'язок між факторною ознакою – часом у русі, та результативною ознакою – продуктивністю праці є не визначеним, та носить лінійний характер.

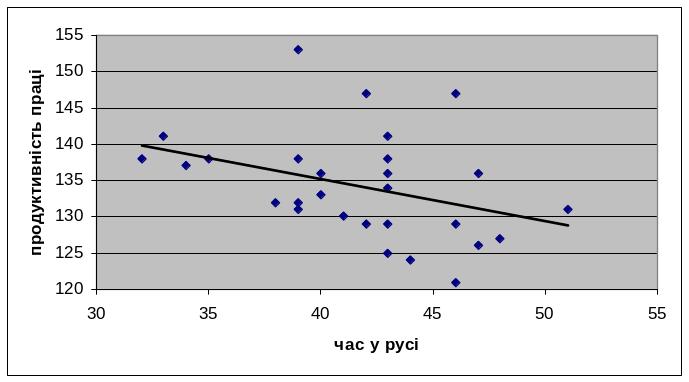
Рис.11 Залежність між часом у русі (год) та

продуктивністю праці (т\год)