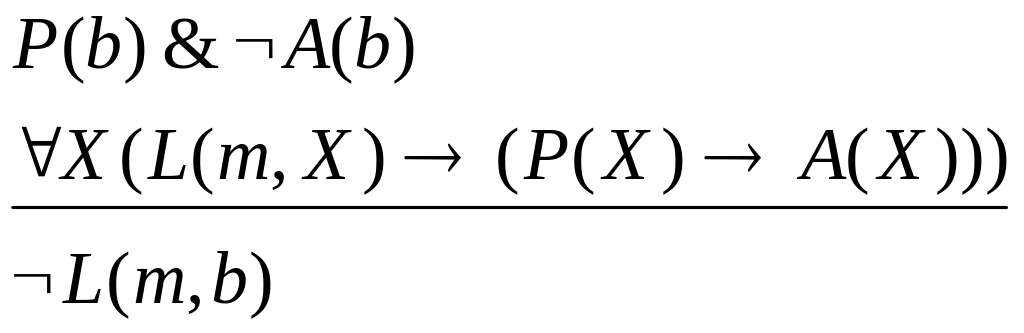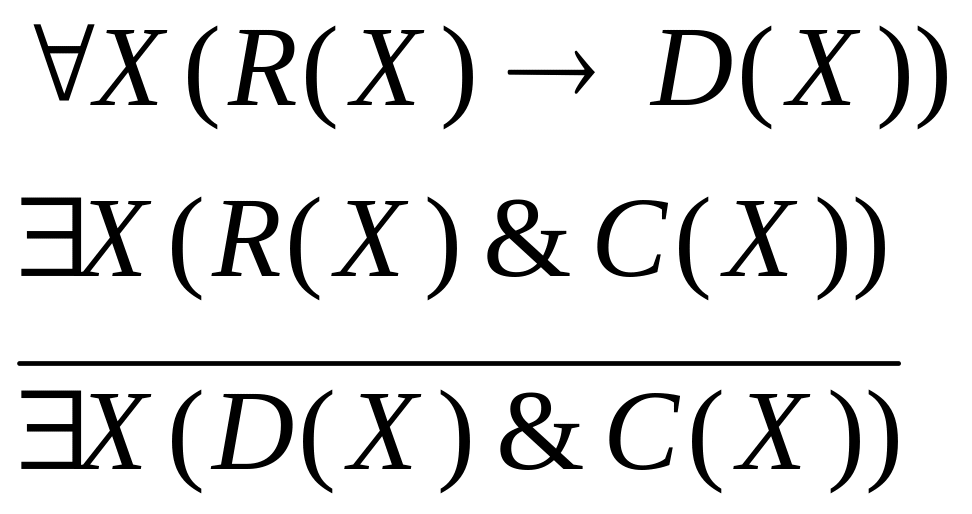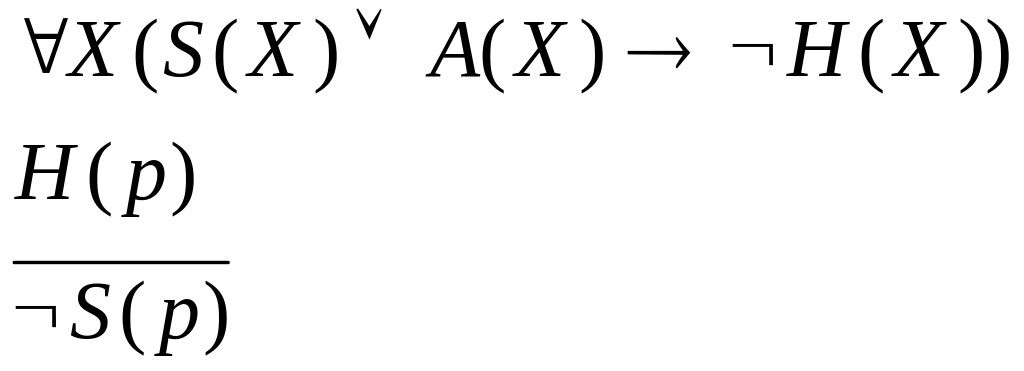2.3. Исчисление предикатов первого порядка как формальная система

Рассмотрим формальную аксиоматическую систему ФС₂ для ис­числения предикатов.

1. Исходными элементами ФС₂ являются:

1. счетное множество предметных переменных x₁, х₂,, … , х_n, . . .;

2. конечное (может быть и пустое) или счетное множество предметных констант a₁, a₂, …;

3. конечное (может быть и пустое) или счетное множество функциональных букв ;

4. непустое конечное или счетное множество предикатных букв ;

5. символы исчисления высказываний: ¬, &, , →;

6. скобки ( ) и запятая;

7. символы , ;

8. других исходных элементов нет.

2. Правила образования ППФ:

1. всякий атом есть ППФ;

2. если А и В – ППФ и х – предметная переменная, то каждое из выражений ¬А, А → В, А & В, А  B, х А и х A есть ППФ;

3. других правил образования ППФ нет.

Таким образом, форма записи ППФ совпадает с записью фор­мул исчисления предикатов.

3. Система аксиом.

К системе аксиом исчисления высказываний добавляются еще две аксиомы:

a12. x A(x)) → A(t), где A(x) есть ППФ и t – терм, свобод­ный для x в A(x).

а13. A(t) → x A(x), где A(x) есть ППФ и t – терм, свобод­ный для x в A(x).

4. Правила вывода.

Правило 1. Все аксиомы выводимы.

Правило 2. Правило подстановки. Это правило аналогично правилу подстановки, которое имело место для исчисления высказываний. Только для ФС₂ мы будем иметь дело с такой подстановкой термов t₁, t₂, …, t_k вместо в A[ ], что A[ ] свободна для t₁, t₂, …, t_k .

Несоблюдение этого условия может привести к неприятным последствиям. Например, пусть в аксиоме 12 терм t не свободен для x в А[x] и пусть А[x] есть ППФ вида ¬x₂A(x₁, x₂) и t есть x₂. Тогда терм t не свободен для x₁ в ¬x₂A(x₁, x₂).

Рассмотрим а12: x₁(¬x₂ A(x₁, x₂)) → ¬₂A(x₂, x₂).

Возьмем в качестве интерпретации любую область, содержащую не менее двух элементов, а в качестве A – отношение тождества. Тогда посылка x₁(¬x₂A(x₁,x₂)) в а12 истинна, а заключение ¬x₂ A(x₂, x₂) ложно.

Правило 3. Правило modus ponens (МР).

Если ├ A и ├ A → В, то ├ B.

Правило 4. Правило обобщения (или правило связывания квантором общности).

Если ППФ B → A(x) при условии, что В не содержит свобод­ных вхождении x, выводима, то выводима будет и ППФ B → x A(x). В дальнейшем это правило будем обозначать че­рез Gen.

Правило 5. Правило конкретизации (или правило связывания кван­тором существования).

Если A(x) → В – выводимая ППФ (теорема) и В не содержит свободных вхождений x, то x A(x) → В также теорема. Обоз­начим это правило через Еx.

Правило 6. Если A – теорема, имеющая квантор общности и/или кван­тор существования, то одна связанная переменная в A может быть заменена другой связанной переменной, отличной от всех свобод­ных переменных, одновременно во всех областях действия кванто­ра и в самом кванторе. Полученная ППФ также является теоремой.

Правило 7. Других правил вывода нет.

Пример 2.5.

Пусть A(x). Доказать x A(x).

Правило, являющееся разновидностью правила вывода Gen, обозначается Gen’.

1. A(x)

2. A(x)(BA(x)) A1

3. BA(x) MP 1,2

4. Bx A(x) Gen

5. Rx A(x) ПС B на R, где R - общезначимая формула

6. R

7. x A(x) MP 5,6

Полученное правило иногда называют производным правилом связывания квантором общности.

Определение выводимости в исчислении предикатов является расширением соответствующего определения для исчисления выска­зываний. Поэтому среди выводимых ППФ исчисления предикатов будут находиться все выводимые ППФ исчисления высказываний.

Будем считать, что ППФ B выводима из ППФ A (аналогично из множества ППФ A₁, …, A_n), если:

1. A выводима из A;

2. каждая выводимая в ФС₂ ППФ также выводима и из A;

3. из выводимости ППФ B₁, и B₁ →B₂ из A следует выводимость B₂ из A;

4. если ППФ B₁ → B₂(x) выводима из A, причем B₁ и A не содержат свободных вхождений x, то и ППФ B₁ →xB₂(x) также выводима из A;

5. если ППФ B₂(x) → B₁ выводима из A. причем B₁ и A не содержат свободных вхождений x, то и ППФ хB₂(x) → B₁ выводима из A;

6. если ППФ B выводима из ППФ A, то и B', полученная из B подстановкой термов вместо свободных вхождений в B перемен­ных, также выводима из A;

7. если B выводима из A. то и B', полученная из B любым переименованием связанных переменных, отличных от имен сво­бодных переменных, выводима из A.

Вывод ППФ из пустого множества посылок есть доказательство этой ППФ. а сама ППФ называется теоремой.

Для исчисления предикатов также имеет место теорема дедук­ции: если A₁, A₂, …, A_n ├ B, то ├ A₁ → (A₂ → (…(A_n → B)…)).

Правила силлогизма, перестановки посылок, объединения и разъединения посылок для исчисления предикатов доказываются аналогично.

Пример 2.6.

Докажем, что xy A(x, y) → yx A(x, y) выводима.

1. ├ y A(x, y) → A(x, t) a12;

2. ├ A(x, t) → w A(w, t) a13;

3. ├ y A(x, y) → w A(w, t) силлогизм из 1 и 2;

4. ├ хy A(x, y) → w A(w, t) Ex;

5. ├ хy A(x, y) → t w A(w, t) Gen;

6. ├ хy A(x, y) → yx A(x, y) пр. 6.

Пример 2.7.

Докажем, что ├ x(A(x) → B(x)) → (x A(x) → x B(x)).

1. ├ x(A(x) → B(x)) → (A(y) → B(y)) а12;

2. x(A(x) → B(x)) ├ A(y) → B(y) теорема дедукции;

3. ├ B(y) → x B(x) a13;

4. x(A(x) → B(x)) ├ A(y) → x B(x) силлогизм из 2 и 3;

5. x(A(x) → B(x)) ├ y A(y) → x B(x) Ex;

6. ├ x(A(x) → B(x)) → (x A(x) → x B(x)) теорема о дедукции и пр. 6.

Остановимся теперь на свойствах исчисления предикатов: не­противоречивости и полноте. Как и раньше, будем считать непроти­воречивым такое исчисление, в котором не выводимы никакие две ППФ, из которых одна является отрицанием другой.

Теорема 2.4. Исчисление предикатов первого порядка непротиворечиво.

Так как аксиомам исчисления предикатов соответствуют выводи­мые ППФ исчисления высказываний, то, очевидно, что всякой вы­водимой ППФ исчисления предикатов соответствует выводимая ППФ исчисления высказываний. Из полноты исчисления высказы­ваний и непротиворечивости исчисления предикатов вытекает, что всякая ППФ исчисления высказываний, выводимая в исчислении предикатов, является выводимой ППФ исчисления высказываний.

Теорема 2.5. Во всяком исчислении предикатов первого поряд­ка всякая теорема является общезначимой ППФ.

Обратное утверждение носит название проблемы полноты исчис­ления предикатов в широком смысле, которая решается положи­тельным образом. Впервые проблему полноты в широком смысле в 1930 г. доказал выдающийся немецкий математик и логик К. Гедель.

Теорема 2.6. (Геделя о полноте). Во всяком исчислении преди­катов первого порядка всякая общезначимая ППФ является тео­ремой.

Что касается проблемы полноты в узком смысле, то для исчис­ления предикатов первого порядка она решается отрицательно. На­помним, что система аксиом называется полной в узком смысле, если нельзя без противоречия присоединить к данной системе никакую другую невыводимую ППФ. Исчисление предикатов оказы­вается неполным в узком смысле, так как к его аксиомам можно присоединить без противоречия недоказуемую в нем следующую ППФ х А(х) →x A(x). Считаем, что преди­кат, входящий в данную ППФ, определен на некоторой области V, состоящей из одного элемента. Тогда данная ППФ вырождается в ППФ вида A → A, которая является выводимой ППФ. Следова­тельно, эта ППФ может быть без противоречия присоединена к аксиомам исчисления предикатов.

До сих пор рассматривалось исчисление предикатов, в котором отсутствовало такое важное понятие, как понятие равенства. Однако во многих формальных системах это понятие используется. Не рас­сматривая этот вопрос подробно, скажем несколько слов об исчис­лении первого порядка с равенством.

Интуитивно понятно, что отношение х = у означает, что х и у – это один и тот же предмет или что х и у – имена одного и того же предмета. Равенство обладает следующими свойствами:

1. оно есть отношение эквивалентности (рефлексивно, симмет­рично и транзитивно);

2. если х = у и А есть результат замены одного или нескольких вхождений х в высказывание В вхождениями у, то А имеет то же значение, что и В (правило замены равного равным).

Свойства симметричности и транзитивности равенства выводятся из рефлексивности и правила замены равного равным.

Для получения исчисления предикатов с равенством добавим в рассмотренное нами исчисление предикатов следующее:

1. в число символов предикатный символ =;

2. в правила конструирования ППФ следующее правило: если х и у – предметные переменные, то х = у – ППФ;

3. в число аксиом следующие две аксиомы:

а14. x₁ (x₁ = x₁) (рефлексивность равенства);

a15. xy((х = у) → (A(x) → A(y))) (подстановочность равен­ства), где х и у – предметные переменные, А(х) – произволь­ная ППФ, а А(у) – ППФ, полученная из А(х) заменой х вхожде­ниями у (необязательно всех) .

Из аксиом а14 и а15 легко доказываются свойства симметричности и транзитивности равенства, т. е. ├ (х = у) → (y = x) и ├ (х = у) → (y = z → x = z).

В заключение этого раздела приведем несколько примеров ФС₂.

Пример 2.8. Теория частичного упорядочения.

Имеем одну предикатную букву A₁. Обозначим A₁(x₁, x₂) и ¬A₁(x₁, x₂)

через х₁ < х₂ и х₁ ≮ х₂.

Система аксиом:

1. x₁ (х₁ ≮ х₁) (иррефлексивность),

2. x₁x₂x₃(x₁ < x₂ & x₂ < x₃ → x₁ < x₃) (транзитивность).

Пример 2.9. Теория групп.

Имеем одну предметную константу а₁, обозначаемую как 0, одну функциональную букву f₁ и одну предикатную букву A₁. Обозначим f₁(x₁, x₂) через x₁ + x₂ и A(x₁, x₂) через x₁ = x₂.

Система аксиом:

1. x₁x₂x₃ (x₁ + (x₂ + x₃) = (x₁ + x₂) + x₃) – ассоциативность;

2. x₁ (0 + x₁ = x₁);

3. x₁ x₂( x₂ + x₁ = 0) – существование обратного элемента;

4. x₁ (x₁ = x₁) – рефлексивность равенства;

5. x₁x₂ ( x₁ = x₂ → x₂ = x₁) – симметричность равенства;

6. x₁x₂x₃ (x₁ = x₂ → (x₂ =x₃→ x₁ = x₃)) – транзитивность равенства;

7. x₁x₂x₃ (x₂ = x₃ → ( x₁+ x₂ = x₁+ x₃ & x₂ + x₁= x₃ + x₁)) – подстановочность равенства.

Если ├x₁x₂( x₁ + x₂ = x₂ + x₁), то группа называется абелевой или коммутативной.

Пример 2.10. Формальная арифметика.

Имеем одну предметную константу a₁ обозначаемую как 0, три функциональные буквы f₁, f₂, f₃ и одну предикатную букву A. Обозначим A(x₁, x₂) через х₁ = х₂, f₁(x) – через x', f₂(x₁, x₂) – че­рез x₁ + x₂ и f₃(x₁,x₂) – через x₁ • x₂.

Система аксиом Пеано:

1. x₁ = x₂ → (x₁ = x₃ → x₂ = x₃);

2. x₁ = x₂ → x'₁ = x'₂;

3. 0  x'₁;

4. x'₁ = x'₂ → x₁ = x₂;

5. x₁ + 0 = x₁;

6. x₁ + x'₂ = (x₁ + x₂)';

7. x₁ • 0 = 0;

8. x₁ • x'₂ = (x₁ • x₂) + x₁;

9. A(0) → (x(A(x) → A(x')) → x A(x)),

где А(x) – произвольная ППФ формальной арифметики, A(0) и А(x') – результаты подстановки, соответственно, 0 и x' вместо сво­бодных вхождений x в А(x) . Интерпретация константы 0 и опера­ций следующая: 0 интерпретируется как число «ноль», x' – как x + 1, x + y – как сумма x и y, x • y – как произведение x и y. Заметим, что аксиомы с 1 по 8 представляют собой конкретные ППФ, а аксиома 9 является схемой аксиом, порождающей беско­нечное множество аксиом. Приведенная схема аксиом есть принцип математической индукции.

Пример 2.11. Доказать средствами ФС2 следующее утверждение на естественном языке: ”Ни один первокурсник не любит второкурсников. Все живущие в общежитии - второкурсники. Следовательно, ни один первокурсник не любит никого из живущих в общежитии”.

x(P(x)y(B(y)L(x,y)))

x(O(x)B(x))

_________________________

x(P(x)y(O(y)L(x,y)))

1. x(P(x)y(B(y)L(x,y)))

P(x)y(B(y)L(x,y)) A12

2. x(O(x)B(x))(O(x)B(x)) A12

3. x(P(x)y(B(y)L(x,y))), P(x) 

y(B(y)L(x,y)) теорема дедукции

4. x(P(x)y(B(y)L(x,y))), P(x) 

y(B(y)L(x,y))(B(y)L(x,y)) A12

5. x(P(x)y(B(y)L(x,y))), P(x) 

B(y)L(x,y) MP 3,4

6. x(O(x)B(x))O(x)B(x) теорема дедукции для 2.

7. y(O(y)B(y))O(y)B(y) ПС x на y

8. x(P(x)y(B(y)L(x,y))), y(O(y)B(y)), P(x)  O(y) L(x,y) сил. 5,7

9. x(P(x)y(B(y)L(x,y))), y(O(y)B(y)), P(x)  y(O(y) L(x,y)) Gen’

10.x(P(x)y(B(y)L(x,y))), y(O(y)B(y)) 

P(x)y(O(y) L(x,y)) теорема дедукции

11. x(P(x)y(B(y)L(x,y))), y(O(y)B(y)) 

x(P(x)y(O(y) L(x,y))) Gen’

Задачи

1. Проверить эквивалентны ли следующие формулы:

1. xF(x) и xF(x)

2. x(F(x)A) и x(F(x)A)

3. x(AF(x)) и AxF(x)

4. x(A&F(x)) и A&xF(x)

5. х(F(x)G(x)) и xF(x)xG(x)

6. AxF(x) и x(AF(x))

7. x(F(x)&G(x)) и хF(x)&xG(x)

8. хF(x) и xF(x)

9. хyzF(x,y,z) и yx (x,y,z)

10. хy (F(x,y) zG(z)) и хyz(F(x,y)G(z))

II. Доказать утверждения средствами ФС2:

1.	Каждый член группы любит логику и программирование. Некоторые члены группы – девушки. Следовательно, существуют девушки, которые любят программирование.
2.	Каждый, кто хранит деньги в сбербанке, получает проценты. Следовательно, если не существует процентов, то никто не хранит деньги в сбербанке.
3.	Ваня - мальчик, у которого нет автомобиля. Марго любит только мальчиков, имеющих автомобили. Следовательно, Марго не любит Ваню.
4.	Ни один республиканец или демократ не является социалистом. Джон- социалист. Следовательно, Джон не республиканец.
5.	Все рациональные числа являются действительными числами. Некоторые рациональные числа - целые числа. Следовательно, некоторые действительные числа - целые числа.
6.	Все первокурсники встречаются со всеми второкурсниками. Ни один первокурсник не встречается ни с одним студентом предпоследнего курса. Существуют первокурсники. Следовательно, ни один второкурсник не является студентом предпоследнего курса.
7.	Ни один преподаватель не является невеждой. Некоторые невежды попадают в институт. Следовательно, некоторые люди, попадающие в институт, не являются преподавателями.
8.	Некоторые первокурсники любят всех второкурсников. Ни один первокурсник не любит никого из студентов последнего курса. Следовательно, ни один второкурсник не является студентом последнего курса.
9.	Каждый, купивший лотерейный билет, получает премию. Следовательно, если нет премий, то никто не покупает билетов.
10.	Всякий разумный философ - циник и только женщины являются разумными философами. Существуют разумные философы. Следовательно, некоторые из женщин - циники.
11.	Всякий, кто находится в здравом уме, может понимать математику. Ни один из сыновей Гегеля не может понимать математику. Сумасшедшие не допускаются к голосованию. Следовательно, никто из сыновей Гегеля не допускается к голосованию.
12.	Для любого множества Х существует множество У, такое, что мощность У больше мощности Х. Если Х включено в У, то мощность Х не больше мощности У. Всякое множество включено в V. Следовательно, V не множество.
13.	Ни один торговец не покупает использованную машину для своей семьи. Некоторые люди, которые покупают использованные машины для своих семей, нечестны. Следовательно, некоторые нечестные люди не являются торговцами.
14.	Все люди добры и благородны. Существуют легкомысленные люди. Следовательно, существуют легкомысленные и благородные люди.
15.	Все люди или добры, или злы. Существуют скупые люди. Следовательно, существуют или скупые или злые люди.
16.	Все студенты нашей группы любят физику или математику. Каждый, кто любит физику, участвует в олимпиаде. Ни один студент нашей группы не участвовал в олимпиаде. Следовательно, в нашей группе все студенты любят математику.
17.	Каждый атлет - силён. Каждый, кто силён и интеллигентен, добьётся в жизни успеха. Петр - атлет и интеллигентен. Следовательно, Петр добьётся в жизни успеха.
18.	Ни один студент или аспирант не является невеждой. Петя - невежда. Следовательно, он не студент.
19.	Все добрые люди являются благородными людьми. Некоторые добрые люди - несчастны. Следовательно, некоторые благородные люди несчастны.
20.	Ни один порядочный человек не обидит беззащитного. Все живущие в домах для престарелых - беззащитные. Следовательно, ни один порядочный человек не обидит никого из живущих в домах для престарелых.
21.	Всякий чуткий человек отзывчив и только женщины являются чуткими людьми. Существуют чуткие люди. Следовательно, некоторые из женщин отзывчивы.
22.	Ни один студент не приобретает с рук подержанный магнитофон. Некоторые люди, которые приобретают с рук подержанные магнитофоны, спекулянты. Следовательно, некоторые спекулянты не являются студентами.
23.	Все студенты – граждане своей страны. Следовательно, голоса студентов на выборах являются голосами граждан.
24.	Все, кто живёт в доме №5, заядлые охотники. Все живущие на соседней улице не увлекаются охотой. Все, кто не живёт в доме №5, рыбаки. Следовательно, все живущие на соседней улице являются рыбаками.
25.	Каждый студент - молод. Каждый, кто молод и активен, занимается спортом. Ваня - студент и активен. Следовательно, Ваня – спортсмен.
26.	Преподаватели принимали экзамены у всех студентов, не являющихся отличниками. Некоторые аспиранты и студенты сдавали экзамены только аспирантам. Ни один из аспирантов не был отличником. Следовательно, некоторые преподаватели были аспирантами.
27.	Все дельфины относятся к китообразным. Ни одна рыба не является китообразной. Следовательно, ни одна рыба не является дельфином.
28.	Холмс подозревал, что убийцей Баскервиля является кто-то из его соседей, а не кто-то из обитателей замка. Подобного же мнения придерживались некоторые из соседей, что наводило на мысль о том, что убийцей мог быть кто-либо из недавно поселившихся в окрестностях замка приезжий. Эту мысль можно было принять в качестве версии, что Холмс и сделал. События показали его правоту.
29.	Таможенники возвращают всех, кто въехал в страну без паспорта. Люди на машинах въехали в страну и были возвращены лишь другими людьми на машинах. Ни один человек на машине не имел паспорта. Следовательно, некоторые таможенники были на машинах.

Рассмотрим варианты формализации задач 1-29.

(Заглавные буквы обозначают переменные, а строчные – константы)

Б1.
Б2.
Б3.
Б4.
Б5.
Б6.
Б7.
Б8.
Б9.
Б10.
Б11.
Б12.
Б13.
Б14.
Б15.
Б16.
Б17.
Б18.
Б19.
Б20.
Б21.
Б22.
Б23.
Б24.
Б25.
Б26.
Б27.
Б28.	A(X) – X-сосед; В(Х) – Х-обитатель замка; С(Y) – Y-убийца; E(X,Y) – X подозревает Y в убийстве; D(Y) – Y-приезжий.
Б29.	E(X) – Х въехал в страну; P(X) – X с паспортом; R(X,Y) – Y возвращает X; D(Y) – Y-таможенник; M(X) – X на машине въехал в страну.