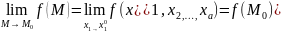11.Асимптомы графика функции.

Аси́мпто́та - кривой с бесконечной ветвью - прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Вертикальнаяасим-птота — прямая вида x=a при условии существования предела .

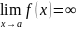Как правило, при определении верти-кальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью опре-делить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. 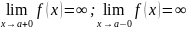. Гори-зонтальная асимптота — прямая вида y=a при условии существования предела 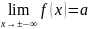. Наклонная асимптота — прямая вида y=kx+b при условии существования пределов 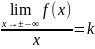; 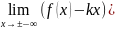=b

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен ∞ ), то наклонной асимптоты при x→+∞ (или )x→-∞ не существует!

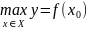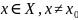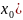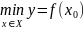12.Наибольшее и наименьшее зна-чение функции на отрезке. Общая схема исследования фун-и и постро-ения графика.Наибольшим значе-нием функции y = f(x) на промежутке X называют такое значение , что для любого , справедливо нераве-нствоf(x)≤f( .Наименьшим значе-нием функции y = f(x) на промежутке X называют такое значение , что для любого справедливо неравенствоf(x)≥f( .Общая схема исследования функции и построения графика. Найти область определения функции. Под областью определения понимается множество всех значений аргумента, при которых функция определена, то есть может быть вычислена.Исследуем общие свойства функции: чётность; нечёт-ность; периодичность. Функция f(x) называется чётной, если f(-x)=f(x). График чётной функции симметричен относительно оси ординат.Функция называется нечётной, если f(-x)=-f(x). График функции симметричен относительно начала координат.Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения. Если существует T такое, что для любого xвыпол-няется условие f(x+T)=f(x), то функция f(x) называется периоди-ческой.Находим точки пересечения графика функции с осями координат.

Абсцисса пересечение с осью Ox ищется исходя из уравнения y=f(x)=0. Ордината пересечение с осью Oy ищется подстановкой значения x=0 в выражение функции y=f(x) Если пересечение с осью Ox найти не удаётся, то обходятся без него. Обычно поиск пересечения с осью Oy не представляет труда.Исследуется непрерывность функции, находятся точки разрыва. Функция f(x) назы-вается непрерывной в точке , если она определена в этой точке и существует предел 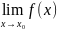, который равен значению функции. То есть 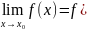). Функция называется непрерывной на проме-жутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка) Точка является точкой разрыва функции, если функция определена и непрерывна в окрестно-сти точки , а в самой точке не явл. непрерывной (хотя может быть опре-делённой). В этом случае говорят, что функция терпит разрыв в точке . Выделяют три типа точек разрыва: устранимый разрыв; конечный разрыв (разрыв первого рода); бесконечный разрыв (разрыв второго рода).Ищутся асимптоты графика функции. Прямая называется асимптотой графика функ-ции, если расстояние от точек графи-ка до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Образно выражаясь, график как бы прилипает к асимптоте. Асимптоты бывают вертикальные, наклонные и горизонтальные. Вертикальные асим-птоты ищутся по точкам разрыва второго рода. Если в точке функ-ция терпит бесконечный разрыв, то вертикальная прямая x= , явл. верти-кальной асимптотой Если хотя бы один из двух пределов не существует (или бесконечен), то соответству-ющей наклонной асимптоты нет.На-ходятся критические точки и интер-валы монотонности. Функция y=f(x) имеет максимум в точке , если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку Функция y=f(x) имеет минимум в точке , если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку . Ищутся точки перегиба и интервалы выпуклости.Для определения точек перегиба находят вторую производную. В точ-ке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая произ-водная отрицательная, то график фун-кции выпуклый вверх.На основании проведённого исследования строим график.Если необходимо вычисляем значение функции в некоторых про-межуточных точках.

13.Понятие функции нескольких независимых переменных. Предел функции двух переменных, непре-рывность.Переменная z (с областью изменения Z) называется функцией 2 независимых переменных х,у в мно-жестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.z = f(x,y), z = z(x,y).

Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных в множе-стве М, если каждому набору чисел 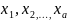из множества М по некото-рому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух перемен-ных.Обозначения: z =f(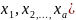 , z = z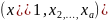 . Предел функции двух переменных .непрерывность.Введем понятие δ-окрестности точки М0 (х0 , у0) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном прост-ранстве как шар радиуса δ с центром в точке М0 (х0 , у0 , z0). Для n-мерного пространства будем называть δ-окрестностью точки М0 . множество точек М с координатами , удовлетворяющими условию p(M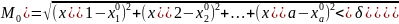

где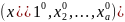 - координаты точки М0. Иногда это множество называют «шаром» в n-мерном пространстве.

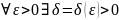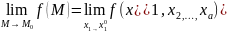Число А называется пределом функ-ции нескольких переменных f . в точке М0, если такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.Обозначения:A= .Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последо-вательными предельными переходами по каждому аргументу в отдельности.

Функция f . называется непрерывной в точке М0 ,если