
- •1.Определение числовой последо-вательности и ее предела. Свойства сходящихся последовательностей.
- •3.Основные правила вычисления пределов. Замечательные пределы.
- •4.Непрерывность функции в точке и на промежутке. Точки разрыва функции и их классификации.
- •5.Производная функции, ее геоме-трический и экономический смысл
- •11.Асимптомы графика функции.
- •14.Частные производные функции двух независимых переменных. Полный дифференциал. Частные производные высших порядков.
5.Производная функции, ее геоме-трический и экономический смысл
Производной
функции y=f(x)
в точке
называется предел отношения приращения
функции в этой точке к приращению
аргумента ∆x
, при ∆x→0
(если этот предел существует иконечен),т.е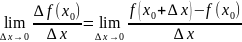 .
Обозначают:
.
Обозначают:
 ,
:
,
:
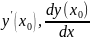 .
Производ-ной
функции в точке справа (слева)
называется
.
Производ-ной
функции в точке справа (слева)
называется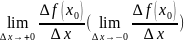 (если
этот предел существует и конечен).
(если
этот предел существует и конечен).
Обозначают:
: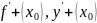 – производная y=f(x) в точке
справа,
– производная y=f(x) в точке
справа,
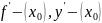 – производная
y=f(x) в точке
слева.Функция
y=f(x)
имеет производную в точке
тогда
и только тогда, когда в этой точке
существуют и равны между собой производные
функции справа и слева. Причем
– производная
y=f(x) в точке
слева.Функция
y=f(x)
имеет производную в точке
тогда
и только тогда, когда в этой точке
существуют и равны между собой производные
функции справа и слева. Причем
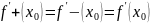 .
Если функция y = f(x) имеет производную
в точке
,
то функция f(x) в этой точке
непрерывна.Геоме-трический смысл. Пусть
на плоскости x0y дана непрерывная кривая
y=f(x)
.
Если функция y = f(x) имеет производную
в точке
,
то функция f(x) в этой точке
непрерывна.Геоме-трический смысл. Пусть
на плоскости x0y дана непрерывная кривая
y=f(x)
Рассмотрим на графике кривой точки Mo(xo;f(xo)) и M1(xo+Dx; f(xo+Dx)). Проведем секущую MoM1. Пусть – угол наклона секущей MoM1 относи-тельно оси 0х. Если сущ. пре-дел , то прямая, проходящая через Mo и образующая с осью 0х угол , называется касательной к графику данной кривой в точке Mo. Таким образом, под касательной к кривой y=f(х) в точке Mo естественно пони-мать предельное положение секущей MoM1, к которому она стремится, когда Dx0. Пусть N(xo+Dx; f(xo)) – точка, дополняющая отрезок MoM1 до прямоугольного треугольника MoM1N. Так как сторона MoNпарал-лельна оси 0х, то переходя к пределу в левой и правой частях этого равенства при Dx→0, получим Поэтому геометрический смысл производной состоит в том, что f’(x0) – это тангенс угла наклона (угловой коэффициент) касательной к графику y=f(х) в точке (xo; f(xo)). Найдём уравнение касательной к графику в точке Mo(xo; f(xo)) в виде y=kx+b. Так как Mo f(x), то должно выполняться равенство f(x0)=kx0+b, откуда b= f(x0) – kx0. Следовательно, касательная задаётся уравнением
y=kx+f(x0) – kx0=f(x0)+k(x – x0).
Поскольку
k=f'(x0), то уравнение касательной имеет
вид y=f(x0)+f'(x0)(x – x0).Экономический смысл.
К предельным величинам в экономике
относятся: предельные издержки,
предельный доход, предельная полезность,
предельная производительность,
предельная скло-нность к потреблению
и т.д. Понятие предельных величин
позволило создать совершенно новый
инстру-мент исследования и описания
эконом.явлений, посредством кото-рого
стало возможно решать научные проблемы,
прежде не решённые или решённые
неудовлетворительно. Все эти величины
самым тесным образом связаны с понятием
производной. Предельные величины
характеризуют не состояние (как суммарная
или средняя величины), а процесс,
изменение экономического объекта.
Следовательно, производная высту-пает
как скорость изменения некото-рого
экономического объекта (про-цесса) с
течением времени или отно-сительно
другого исследуемого фактора.Предельные
издержки МС (marginalcosts) выражают
дополни-тельные затраты на производство
каждой дополнительной единицы
продукции,где
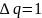 .
Используя равенствоMC=TC(
.
Используя равенствоMC=TC(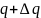 )предель-ные
издержки есть не что иное, как первая
производная от совокупных издержек,
если последние предста-влены как функция
от выпускаемого количества
продукции.Предельная выручка MR
(marginalrevenue)
– это дополнительный доход, полученный
при переходе от производства n-ной
к (n+1)-ой
единице продукта. Она представляет
собой первую производную от выручки:
)предель-ные
издержки есть не что иное, как первая
производная от совокупных издержек,
если последние предста-влены как функция
от выпускаемого количества
продукции.Предельная выручка MR
(marginalrevenue)
– это дополнительный доход, полученный
при переходе от производства n-ной
к (n+1)-ой
единице продукта. Она представляет
собой первую производную от выручки:
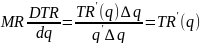 .
Для
хозяйствующее-го субъекта, который
действует в условиях совершенной
конкуренции: TR
= P*Q,
где TR
– выручка (totalrevenue);
P
– цена (price).
Таким образом
.
Для
хозяйствующее-го субъекта, который
действует в условиях совершенной
конкуренции: TR
= P*Q,
где TR
– выручка (totalrevenue);
P
– цена (price).
Таким образом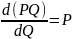 , Þ MR=
P.
Это равенство верно для рынка совершен-ной
конкуренции.Любой индивид испол.свой
доход Y
после уплаты налогов на потребление C
и сбере-жениеS.
Ясно, что лица с низким доходом целиком
используют его на потребление, а на
сбережение средств не остается. С ростом
дохода субъект не только больше
потребляет, но и больше сберегает. Как
установлено экономической наукой,
потребление и сбережение зависят от
размера дохо-да:Y=
C(Y)
+ S(Y).Использование
производной позволяет определить такую
категорию, как предельную склонность
к потреблению MPC
(marginalpropertytoconsume),
показывающую долю прироста
лич-ногопотребления в приросте дохода:
, Þ MR=
P.
Это равенство верно для рынка совершен-ной
конкуренции.Любой индивид испол.свой
доход Y
после уплаты налогов на потребление C
и сбере-жениеS.
Ясно, что лица с низким доходом целиком
используют его на потребление, а на
сбережение средств не остается. С ростом
дохода субъект не только больше
потребляет, но и больше сберегает. Как
установлено экономической наукой,
потребление и сбережение зависят от
размера дохо-да:Y=
C(Y)
+ S(Y).Использование
производной позволяет определить такую
категорию, как предельную склонность
к потреблению MPC
(marginalpropertytoconsume),
показывающую долю прироста
лич-ногопотребления в приросте дохода:
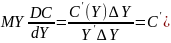 ).
По
мере увеличения доходов MPCумень-шается.
Долю прироста сбережений в приросте
дохода показывает предель-ная склонность
к сбережению MPS
(marginal propensity to save):
).
По
мере увеличения доходов MPCумень-шается.
Долю прироста сбережений в приросте
дохода показывает предель-ная склонность
к сбережению MPS
(marginal propensity to save):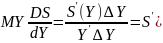 ).
).
6.Правила
дифференцирования функций. Логарифмическое
диффе-ренцирование. Производные выс-ших
порядков.К
основным правилам дифференцирования
относят:вынесе-ние постоянного множителя
за знак производной;производная
произве-дения функций;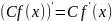 ,
C
,
C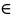 R.
Произвольный множитель мож-но выносить
за знак предельного перехода (это
известно из свойств предела), поэтому
R.
Произвольный множитель мож-но выносить
за знак предельного перехода (это
известно из свойств предела), поэтому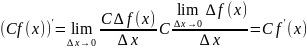
производная
суммы, производная разности;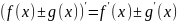 ,
производная произведения фун-кций
,
производная произведения фун-кций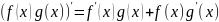 ,
производная
частного двух функций(производная
дроби).
,
производная
частного двух функций(производная
дроби).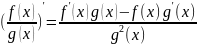 .
Логарифми-ческим дифференцированием
назы-вается метод дифференцирования
функций, при котором сначала находится
логарифм функции, а затем вычисляется
производная от него. Такой прием
позволяет эффективно вычислять
производные степенных и рациональных
функций. Рассмотрим этот подход более
детально. Пусть дана функция y = f(x).
Возьмем нату-ральные логарифмы от обеих
частей:
.
Логарифми-ческим дифференцированием
назы-вается метод дифференцирования
функций, при котором сначала находится
логарифм функции, а затем вычисляется
производная от него. Такой прием
позволяет эффективно вычислять
производные степенных и рациональных
функций. Рассмотрим этот подход более
детально. Пусть дана функция y = f(x).
Возьмем нату-ральные логарифмы от обеих
частей:
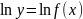 .
Теперь
продифферен-цируем это выражение как
сложную функцию, имея ввиду, что y - это
функция от x.
.
Теперь
продифферен-цируем это выражение как
сложную функцию, имея ввиду, что y - это
функция от x.

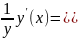 .
Отсюда
видно, что искомая производная равна
.
Отсюда
видно, что искомая производная равна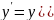 .
Производные
высшихпо-рядков явно заданной функции
.
Производные
высшихпо-рядков явно заданной функции
Производная
у'=ƒ'(х) функции у=ƒ(х) есть также функция
от х и называется производной первого
порядка.Если функция ƒ'(х) дифференцируема,
то ее производная называется производной
второго порядка и обозначается у"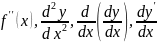 .
Итак,
у"=(у')'.
.
Итак,
у"=(у')'.
Производная от производной второго порядка, если она существует, назы-вается производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'. Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:y(n)=(y(n-1))¢. Производные порядка выше первого называются производными высших порядков.Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).
7.Правило
Лопиталя для раскрытия неопределенностей
вида
и
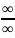 .
Раскрытие неопределенностей вида
.
Раскрытие неопределенностей вида
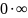 ;
;
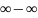 ;
;
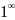 ;
;
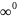 ;
;
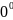 .В
математическом анализе правилом
Лопита́ля называют метод нахож-дения
пределов функций, раскры-вающий
неопределённости вида 0 / 0 и ∞/∞.
Обосновывающая метод теоре-ма утверждает,
что при некоторых условиях предел
отношения функций равен пределу
отношения их произво-дных.Правило
говорит, что если фун-кции f(x) и g(x)
обладают следующим набором условий:
.В
математическом анализе правилом
Лопита́ля называют метод нахож-дения
пределов функций, раскры-вающий
неопределённости вида 0 / 0 и ∞/∞.
Обосновывающая метод теоре-ма утверждает,
что при некоторых условиях предел
отношения функций равен пределу
отношения их произво-дных.Правило
говорит, что если фун-кции f(x) и g(x)
обладают следующим набором условий:
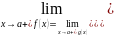 .
Или
.
Или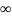 ;
;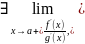
 в
некоторой окрестности точки a,тогда
существует
в
некоторой окрестности точки a,тогда
существует
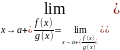 .
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).Неопреде-ленности типа
0*∞ и ∞-∞ также целесообразно приводить
к виду 0/0 следующимипреобразованиями
.
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).Неопреде-ленности типа
0*∞ и ∞-∞ также целесообразно приводить
к виду 0/0 следующимипреобразованиями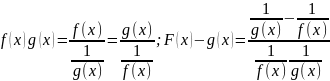 . Для раскрытия неоп-ределенностей типа
;
;
.Целе-сообразно
первоначально прологари-фмировать
выражения, предел которых требуется
найти.Дру-гим общим методом раскрытия
неопреде-ленностей типа
и
и
сводимых к ним является Лопита ля
правило.
. Для раскрытия неоп-ределенностей типа
;
;
.Целе-сообразно
первоначально прологари-фмировать
выражения, предел которых требуется
найти.Дру-гим общим методом раскрытия
неопреде-ленностей типа
и
и
сводимых к ним является Лопита ля
правило.
8.Дифференциал функции. Связь дифференциала и производной. Испол.дифференциала в приближе-нныхвычислениях.Дифференциа-лом функции у=ƒ(х) в точке х называется главная часть ее прира-щения, равная произведению произво-дной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х. Дифференциал dу называют также дифференциалом первого порядка. Найдем дифферен-циал независимой переменной х, т. е. дифференциал функции у=х.Так как у'=х'=1, то, согласно формуле имеем dy=dx=∆x, т. е. дифференциал незави-симой переменной равен приращению этой переменной: dх=∆х.Поэтому формулу можно записать так: dy=ƒ'(х)dх, иными словами, диффе-ренциал функции равен произве-дению производной этой функции на дифференциал независимой перемен-ной.Из формулы следует равенство dy/dx=ƒ'(х). Теперь обозначение
Производной dy/dx можно рассма-тривать как отношение дифферен-циаловdy и dх.Связь дифференциала и производной. Производной функции f(x) в точке x0 называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно мало). Записывается так.
LimΔx→0 (Δf(x0)/Δx)=limΔx→0 ((f(x+Δx)-f(x0))/Δx)=f`(x0). Нахожде-ние производной называется диффе-ренцированием. Вводится опреде-ление дифференцируемой функции: Функция f, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой на данном промежутке. Применение дифференциала к приближенным вычислениям. Использование диффе-ренциала в приближенных вычис-лениях, как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, причем это равенство тем точнее, чем меньше ∆х. Это равенство позволяет с большой точностью вычи-слить приближенно приращение лю-бой дифференцируемой функции.
9.Исследование на монотонность функции одной переменной. Точки экстремума. Необходимые и недо-статочные условия сущ. экстре-мума.Моното́ннаяфу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неполо-жительное. Если в дополнение прира-щение не равно нулю, то функция называется стро́гомоното́нной. Моно-тонная функция — это функция, меняющаяся в одном и том же направлении. Функция возрастает, если большему значению аргумента соответствует большее значение фун-кции. Функция убывает, если больше-му значению аргумента соответствует меньшее значение функции.Если функция возрастает или убывает на некотором промежутке, то она назы-ваетсямонотонной на этом проме-жутке. Если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.
Свойства
монотонных функций. Сум-ма нескольких
возрастающих функ-ций является
возрастающей функ-цией.Произведение
неотрицательных возрастающих функций
есть возра-стающая функция.Если функция
f возрастает, то функции cf (c > 0) и f + c
также возрастают, а функция cf (c < 0)
убывает. Здесь c – некоторая конс-танта.Если
функция f возрастает и сохраняет знак,
то функция 1/f убывает.Если функция f
возрастает и неотрицательна, то fn где
n ∈
N, также возрастает.Если функция f
возрастает и n – нечетное число, то fn
также возрастает.Композиция g (f (x))
возрастающих функций f и g также
возрастает.Точки максимума и мини-мума
называются точками экстре-мума, а
значения функции в этих точ-ках - ее
экстремумами. Промежутки возрастания
и убывания. Функция f(x) называется
возрастающей на проме-жутке D, если для
любых чисел x1 и x2 из промежутка D таких,
что x1 < x2, выполняется неравенство
f(x1) < f(x2).Функция f(x) называется убыва-ющей
на промежутке D, если для любых чисел
x1 и x2 из промежутка D таких, что x1 < x2,
выполняется неравенство f(x1) >
f(x2).Необходи-мые условия экстремума.
Если точка xо является точкой экстремума
функции f(x), то либо f '(xо) = 0, либо f (xо) не
существует. Такие точки называют
критическими, причем сама функция в
критической точке определена. Экстремумы
функ-ции следует искать среди ее
крити-ческих точек.Первое достаточное
условие. Пусть xо - критическая точка.
Если f ' (x) при переходе через точку xо
меняет знак плюс на минус, то в точке
xо функция имеет max,
в противном случае - min.
Если при пе-реходе через критическую
точку производная не меняет знак, то в
точ-кеxо экстремума нет.Второе доста-точное
условие. Пусть функция f(x) имеет
производнуюf ' (x) в окрестности точки
xо и вторую производную
 в самой точке xо. Если f ' (xо) = 0,
>0
(
<0),
то точка xо является точкой локального
минимума (максимума) функции f(x). Если
же
=0,
то нужно либо пользоваться первым
достаточным условием, либо прив-лекать
высшие производные.На отрезке [a,b]
функция y = f(x) может достигать наименьшего
или наиболь-шего значения либо в
критических точках, либо на концах
отрезка [a,b].
в самой точке xо. Если f ' (xо) = 0,
>0
(
<0),
то точка xо является точкой локального
минимума (максимума) функции f(x). Если
же
=0,
то нужно либо пользоваться первым
достаточным условием, либо прив-лекать
высшие производные.На отрезке [a,b]
функция y = f(x) может достигать наименьшего
или наиболь-шего значения либо в
критических точках, либо на концах
отрезка [a,b].
10.Исследование
функции на выпу-клость и вогнутость.
Точки переги-ба.Дифференцируемая
функция на-зывается выпуклой вниз на
интервале Х, если ее график расположен
не ниже касательной к нему в любой точке
интервала Х.Дифференци-руемая функция
называется выпуклой вверх на интервале
Х, если ее график расположен не выше
касательной к нему в любой точке
интервала Х.Вы-пуклую вверх функцию
часто называют выпуклой, а выпуклую
вниз – вогнутой.Точка называется
точкой перегиба графика функции y =
f(x), если в данной точке существует
касательная к графику функции (она
может быть параллельна оси Оу) и
существует такая окрестность точки ,
в пределах которой слева и справа от
точки М график функции имеет разные
направления выпуклости. Дру-гими
словами, точка М называется точкой
перегиба графика функции, если в этой
точке существует касса-тельная и график
функции меняет направление выпуклости,
проходя через нее.Необходимое условие
сущ. точки перегиба: если функция f(x),
дважды дифференцируемая в некото-рой
окрестности точки
, имеет в
точку перегиба, то
=0
.Первое достаточное условие существования
точки перегиба: если функция f(x) в
некоторой окрестности точки xk-раз
непрерывно дифференцируема, при-чем k
нечётно и k≥3
, и
 при n=2,3,…,k-1
а
при n=2,3,…,k-1
а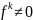 , то функцияf(x)
имеет в
точку перегиба.Второе достаточное
условие существования точки перегиба:
Если в некоторой точке вторая производная
функции равна нулю, а третья не равна
нулю, то эта точка является точкой
перегиба.
, то функцияf(x)
имеет в
точку перегиба.Второе достаточное
условие существования точки перегиба:
Если в некоторой точке вторая производная
функции равна нулю, а третья не равна
нулю, то эта точка является точкой
перегиба.
