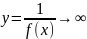1.Определение числовой последо-вательности и ее предела. Свойства сходящихся последовательностей.

Если каждому натуральному числу n=1,2,3,… по какому-то закону поставлено в соответствие вещест-венное число , то множество чисел назыв.числовойпоследовательн-ю.

Число A называется пределом числовой последовательности {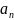 } , если для любого числа 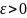, 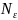сущ. такой номер числовой последова-тельности , зависящий от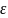 , что для всех номеров числовой последо-вательности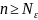 выполняется условие 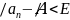.Последо-вательность, которая имеет предел, называется сходящейся. В этом случае пишут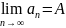 .Сходя-щейсяназыв.последовательность, если она имеет предел. Если последовательность не имеет предела, то она назыв.расходящейся. Свойства сходящихся последовательностей

Теорема 1:Всякая сходящаяся после-довательность имеет только один предел.Доказательство:Предполо-жим, что последовательность {xn} имеет два предела (а ≠ b)xn → a, следовательно xn = a + αn, где αn элемент бесконечно малой последо-вательности; xn → b, следовательно xn = b + βn, где βn элемент бесконечно малой последователь-ности;Оценим разность данных равенств 0 = a – b + (αn - βn), обозначим αn - βn = γn, γn – элемент бесконечно малой последователь-ности, следовательно, γn = b – a,а это означает, что все элементы бесконечно малой последователь-ности равны одному и тому же числу b – a, и тогда b – a = 0 по свойству бесконечно малой последователь-ности, следовательно, b = a, следовательно, последовательность не может иметь двух различных пределов.Теорема 2:Если все эле-менты последовательности {xn} равны С (постоянной), то предел пос-ледовательности {xn}, тоже равен С.

Доказательство:Из определения пре-дела, следует, С = С + 0.Теорема 3:

Если последовательности {xn} и {уn} сходятся, то и последовательность {xn + уn} также сходится и её предел равен сумме её слагаемых (пределов).

Доказательство:xn → a, след.xn = a + αnуn → b, след.уn = b + βn

xn + уn = а + b + (αn + βn) обозначим αn - βn = γn, следовательно xn + уn = а + b + γn, γn элемент бесконечно малой последовательности; след.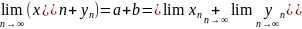 Следствие: разность двух сходящихся после-довательностей есть последова-тельность сходящаяся, и её предел равен разности их пределов.Теорема 4:Если последовательности {xn} и {уn} сходятся, то и последова-тельность {xn * уn} также сходится и её предел равен произведению её множителей (пределов).Доказатель-ство:xn → a, следовательно xn = a + αn уn → b, следовательно уn = b + βn

xn * уn = (а + αn)*(b + βn)=аb+(а βn + bαn + αnβn) обозначим γn = а βn + bαn + αnβn, где γn элемент бесконечно малой последователь-ности, получаетсяxn * уn = ab+ γn, следовательно,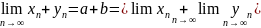 Теорема 5:Если последовательности {xn} и {уn} схо-дятся к числам а и b соответственно, и если b ≠ 0, предел частного {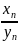 сущ., конечен и равен частному пределов.

2.Предел функции одной перемен-ной в точке. Односторонние пределы. Бесконечно большие и бесконечно малые функции.Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε> 0 существует δ> 0 такое, что для всех x, удовлетворяющих условию |x – a| <δ, x ≠ a, выполняется неравенство |f (x) – A| <ε.Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности {xn} такой, что xn≠a, сходящейся к числу a, соответствующая последо-вательность значений функции{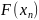 } сходится к числу A.Одно-сторонние пределы. Число А назы-вается левым пределом функции f (x) в точке х0, если для любого как угодно малого положительного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента меньших чем х0 и отличающихся от него на величину меньшую δ, значения функции отличаются от числа А на величину, меньшую чем ε:( ε > 0 ) ( δ = δ (ε) > 0 ) ( x0 - δ < x < x0) : | f (x) – A | < ε. Число B называется правым пределом функции f (x) в точке х0, если для любого как угодно малого положи-тельного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента больших, чем х0 и отличающихся от него на величину меньшую чем δ, значения функции отличаются от числа В на величину, меньшую чем ε:( ε > 0 ) ( δ = δ (ε) > 0 ) ( x0< x < x0+ δ) : | f (x) – В | < ε Левый и правый пределы функции в данной точке условно записывают как 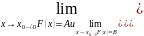Последовательность с бесконечным пределом назыв.бесконечно большой.

Теорема. Функция f (x) имеет в точке х0 конечный предел тогда и только тогда, когда в этой точке существуют конечные правый и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.Бесконечно большие и бес-конечно малые функции.Бесконечно малые функции.Определение. Фун-кция f(x) называется бесконечно малой при х→а, где а может быть числом или одной из величин ∞, +∞ или -∞ , если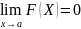 . Беско-нечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.Теорема. Для того, чтобы функция f(x) при х→а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x), где a(х) – бесконечно малая при х→а (a(х)→0 при х→а).Свойства бесконечно малых функций. Сумма фиксированного чис-ла бесконечно малых функций при х→а тоже бесконечно малая функция при х→а.Произведение фиксирован-ного числа бесконечно малых функций при х→а тоже бесконечно малая функция при х→а.Произве-дение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х→а.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.Бесконечно большие функции и их связь с бесконечно малыми

Определение. Предел функции f(x) при х→а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число ∆>0, что неравенство |f(x)|>M выполняется при всех х, удовлетвор-х условию 0 < |x - a| <∆Записывается .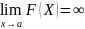 Определение. Функ-ция называется бесконечно большой при х→а, где а – число или одна из величин ∞, +∞ или -∞, если , где А – число или одна из величин ∞, +∞ или -∞.Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.Теорема. Если f(x)→0 прих→а (если х→∞ ) и не обращается в ноль, то