
Зміст
1 Отримання математичного опису об’єкту управління 4
2 Аналіз стійкості САУ без наявності регулятора (корегуючого пристрою) 6
3 Розрахунок настроювань по показнику коливання (методом В.Я. Ротача) 9
4 Розрахунок параметрів настроювання стандартного регулятора 13
Література 17
1 Отримання математичного опису об’єкту управління
Отримання передаточної функції об’єкту управління на основі апроксимації “кривої розгону” з використанням методу Сімою.

Рисунок 1 – Крива розгону об’єкту управління
Нормування кривої розгону:
Із ординат кривої розгону формую вектор-строку вихідних даних:

y ( 0.3 0.31 0.325 0.357 0.39 0.42 0.455 0.48 0.5 0.52 0.54
0.545 0.553 0.56 0.563 0.567 0.57 0.572 0.576 0.578 0.58 ) .
( 0.3 0.31 0.325 0.357 0.39 0.42 0.455 0.48 0.5 0.52 0.54
0.545 0.553 0.56 0.563 0.567 0.57 0.572 0.576 0.578 0.58 ) .
Тепер
отримаю криву розгону без впливу на неї
вхідної дії. Для цього вектор-рядок
початкових даних ділимо на зовнішній
вплив
 ,
і отримуємо вектор – рядок
,
і отримуємо вектор – рядок
 .
.

Від
отриманих значень віднімаю 15
і в результаті отримаю нормований
вектор-рядок
 :
:

Транспоную вектор-строку в вектор-стовпець, нормую криву розгону ( ділю значення на yуст= 14 ) і визначаю розмірність вектора N:

N = 20
1.2
Задаюсь видом передатної функції. По
зовнішньому вигляду кривої розгону
бачу, що при t
= 0 y
= 0 і
 ,
а отже, n
– m
= 1.
,
а отже, n
– m
= 1.
1.3
Задаю крок розрахунку
по часу Δt
=
1,25с та
встановлюю значення коефіцієнта
 для
забезпечення можливості автоматизації
моїх розрахунків. Записую функцію в
MathCad,
яка описує підінтегральний вираз
рівняння для знаходження коефіцієнтів
SK
в загальному вигляді в дискретній
формі:
для
забезпечення можливості автоматизації
моїх розрахунків. Записую функцію в
MathCad,
яка описує підінтегральний вираз
рівняння для знаходження коефіцієнтів
SK
в загальному вигляді в дискретній
формі:

де k – номер обчислюваного коефіцієнта Sk ;
і – номер кроку розрахунку за часом.
1.4 За допомогою пакета MathCad проводжу розрахунок перших 5-ти коефіцієнтів S.

Згідно розрахунків отримав 5-ть перших коефіцієнти:
S1= 7.942;
S2= -24.503;
S3= 68.328;
S4= -89.719;
S5= -181.316.
Оскільки коефіцієнт S2 негативний, то можна обмежитись першим.
А так як прийнято, що різність між степенями знаменника і чисельника дорівнює одиниці, то, очевидно, що порядок чисельника m в нашому випадку повинен дорівнювати 0(тобто, в чисельнику константа), а коефіцієнти будуть співвідноситись як:
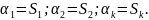
Опираючись
на попереднє пояснення
 буде дорівнювати:
буде дорівнювати:
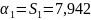
Таким чином, передатна функція об’єкта може буде представлена в вигляді:

2 Аналіз стійкості сау без наявності регулятора (корегуючого пристрою)
Дослідження замкненої системи на стійкість за критерієм Михайлова.
Передатна функція розімкненої системи:

2.1 Замикаю об’єкт управління від’ємним зворотнім зв’язком та знаходжу передатну функцію отриманої системи:

2.2 Характеристичний поліном системи (вираз в знаменнику):

2.3 Виконую заміну s=jω, в результаті отримаю функцію Михайлова:

2.4
Розділивши коефіцієнти, які містять
уявну одиницю, і які її не містять,
отримую вираз для реальної та уявно
частин функції Михайлова

 ;
;
 .
.
2.5 Для отримання годографів Михайлова використовую математичний пакет MathCad:
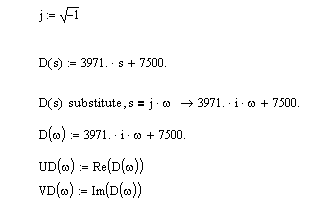
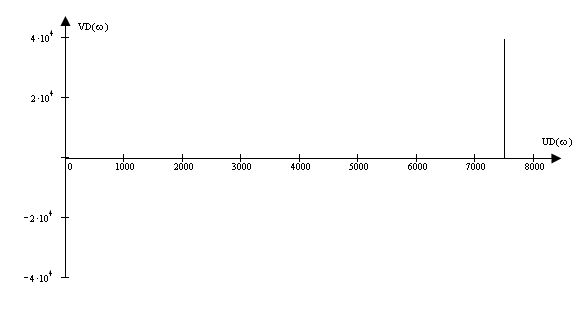
Рисунок 2 – Годограф Михайлова для системи 1-го порядку
Висновок: Дана замкнена система стійка, оскільки кількість пройдених квадрантів годографом відповідає порядку системи. Годограф починається в 1-ому квадранті, в ньому же і уходить в нескінченність.
2.6 Побудова перехідної характеристики замкненої системи та визначення основних показників якості.
2.6.1
Задаю передатну функцію замкненої
системи:
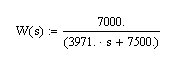 .
.
2.6.2 Виконую перетворення Лапласа передатної функції замкненої системи під дією одиничного ступінчатого сигналу:
![]()
2.6.3
Отримую перехідну функцію:
![]() .
.
2.6.4 Будую перехідну характеристику за допомогою MathCad для t = 7c:
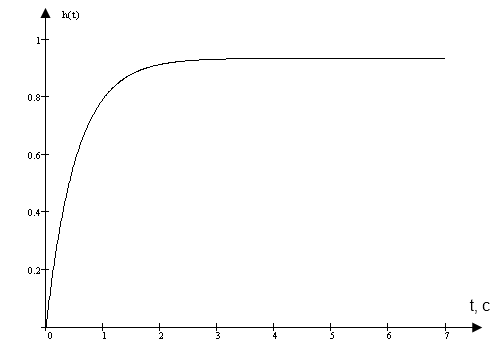
Рисунок 3 – Перехідна характеристика замкненої системи
Перерегулювання σ, % , знаходжу за формулою:

Перехідний процес монотонний, тому перерегулювання відсутнє.
Час
перехідного процесу
 , c,
визначу
із умови:
, c,
визначу
із умови:
 h(t)-
h(t)-
Знайду
5%
коридор від встановленого значення
 :
:

h(t )= 0.93-0.047 = 0.883
tp = 1.55c
Таблиця 1 – Прямі показники якості замкненої системи
№ |
Показник якості |
Одиниця виміру |
Чисельне значення |
1 |
Перерегулювання |
σ, % |
0 |
2 |
Час перехідного процесу |
, c |
1.55c |
