4. Введение в теорию нелинейных колебаний

Выше рассматривалась система, в которой существовали малые отклонения от положения равновесия и движение, описывалось линейными уравнениями. Так в автоматическом управлении для исследования устойчивости состояний равновесия используются

линеаризованные уравнения, описывающие малые возмущения движения, происходящие вблизи названных состояний. Такой анализ позволяет уловить лишь начальные тенденции возмущенного движения, но в случаях неустойчивости не дает возможности проследить все дальнейшее развитие процесса движения при возрастании отклонений и скоростей.

Возмущенные движения с развившимися большими отклонениями в принципе невозможно исследовать с помощью линеаризованных уравнений: нелинейные члены уравнений, будучи пренебрежимо малыми, при малых отклонениях системы от состояния равновесия, начинают играть все более заметную роль при увеличении отклонений. Во многих случаях возрастание колебаний постепенно замедляется, и движение стремится к некоторому устойчивому режиму с постоянными амплитудами - режиму установившихся автоколебаний.

В общих чертах природу этого явления можно понять, рассматривая например, колебательную систему с трением, когда характеристика трения описывается нелинейной функцией скорости:

R = - b₁∙ + b₃∙ , (50)

где: b₁ и b₃ - положительные постоянные. При этом дифференциальное уравнение движения имеет вид:

а· - b₁∙ + b₃∙ + с·q = 0. (51)

Если отклонения очень малы, то нелинейным членом (содержащем ) можно пренебречь; тогда обнаруживается неустойчивость системы вследствие эффекта отрицательного трения. Таким образом, сколь угодно малые начальные возмущения вызовут постепенно возрастающие колебания. Но при этом будет увеличиваться демпфирующее влияние нелинейного члена уравнения, так что рост колебаний станет замедляться и движение будет стремиться к установившемуся режиму с постоянными амплитудами. Описанный процесс иллюстрируется на рис. 8.

q

0

t

t_уст

Рис. 8

5. Успокоители приборных систем

В условиях эксплуатации подвижная система прибора и прибор в целом могут совершать колебания. Колебания в большинстве случаев являются нежелательными, так как могут быть причиной снижения точности показаний прибора, затруднить отсчет их по шкале, а в некоторых случаях привести к полному отказу прибора в работе. В системах совершаются колебания собственные и вынужденные.

Предположим, что измеряемая величина изменилась и приобрела новое значение. В этом случае нарушится равновесие вращающего и противодействующих моментов, действовавших на подвижную систему. Разность между этими моментами, называемая устанавливающим моментом, приводит систему к новому положению равновесия. При подходе к этому положению подвижная система обладает какой-то скоростью и запасом кинетической энергии.

Вследствие этого она может перейти положение равновесия и затем под действием устанавливающего момента возвратиться к положению равновесия и снова перейти его. Таким образом, подвижная система может совершать колебания относительно положения равновесия (собственные колебаниями системы). Такого же рода колебания наблюдаются в том случае, если упругую систему отклонить от положения равновесия ударом или временно действующей внешней возмущающей силой. Чтобы собственные колебания системы затухали, применяют устройства, называемые успокоителями. Создаваемое ими торможение обычно пропорционально скорости движения подвижной системы и направлено в сторону, противоположную скорости движения.

Затуханию колебаний подвижной системы способствует также наличие трения в подвижных соединениях. Однако увеличение трения в подвижной системе нежелательно, так как приводит к увеличению застоя прибора, т.е. к нечувствительности.

Рассмотрим в качестве примера колебание подвижной системы прибора, предназначенного для измерения ускорения (см. рис.9). Чувствительным элементом прибора является масса m груза 1, помещённого на рычаге 2. Момент, создаваемый грузом относительно оси вращения, уравновешиваются моментом, развиваемым спиральной пружиной 3. К рычагу прикреплён поршень воздушного успокоителя 4.

a

m ● ●

α

●

Рис. 9

Такая система может поворачиваться только вокруг оси вращения рычага, и её положение определяется одной координатой - углом поворота α. Следовательно, система имеет одну степень свободы.

За начальное положение равновесия примем горизонтальное положение рычага. На массу m , кроме силы тяжести, действует сила инерции, вызванная ускорением a, которое может быть постоянным или переменным. Уравнение движения подвижной системы может быть найдено из закона механики, согласно которому сумма всех моментов, действующих на тело, включая и моменты инерции, должна быть равна нулю.

В рассматриваемой системе действуют моменты: инерционный, успокоения, пружины, трения и внешний момент, пропорциональный измеряемому ускорению. Уравнение движения подвижной системы имеет вид:

J·d² α /dt² + c·dα /dt + K· α ± M_т = M_вн  (52)

где: α - угол поворота подвижной системы; J·d²α /dt² - инерционный момент; J - момент инерции подвижной системы относительно оси вращения; c·dα /dt - момент, создаваемый успокоителем (момент успокоения); c - коэффициент успокоения, численно равный моменту успокоения при угловой скорости подвижной системы, равной единице, т.е. при скорости в один радиан в секунду: (dα /dt = 1); K· λ - момент пружины; К - жёсткость пружины, численно равная моменту пружины при угле закрутки её на один радиан; M_т - момент трения подвижной системы; M_вн - внешний момент от действия на подвижную систему сил инерции от измеряемого ускорения.

Рассмотрим несколько частных случаев движения, описываемого этим уравнением, причём во всех случаях момент трения будем считать равным нулю. Предположим вначале, что система не имеет успокоителя, а моменты внешних сил и трения равны нулю. Тогда уравнение примет вид:

J·d²α /dt² + K·α = 0;

разделив это выражение на J, получим:

d²α /dt² + K·α / J = 0. (53)

Решением дифференциального уравнения (53) будет:

α =  α₀· сos ( t), (54)

где: α₀ - угол отклонения от начального положения равновесия при t = 0 и dα /dt = 0. Наибольшее отклонение системы за полпериода, равное α₀ называют амплитудой колебания.

Уравнение показывает, что подвижная система, будучи выведенной, из положения равновесия на величину α₀, совершает затем незатухающие колебания по закону косинуса (см. рис. 1).

Время, в течение которого система, совершив одно полное колебание, снова вернется к начальному положению, будет в рассматриваемом примере периодом собственных колебаний, который обозначается Т₀. Период Т₀ можно определить из уравнения (54) приравняв, значения аргумента у косинуса 2π и заменив t на Т₀. Тогда:  

· Т₀ = 2π,

откуда:

Т₀ =2π/ . (55)

Из уравнения следует, что период собственных незатухающих колебаний зависит только от момента инерции J системы и жёсткости К пружины. Чем больше момент инерции и меньше жёсткость пружины, тем больше период колебаний и, следовательно, медленнее движется подвижная система прибора.

Величину, обратную периоду Т₀, называют собственной частотой незатухающих колебаний и обозначают f₀:

f₀ = 1/ Т₀ = (1/2π)· . (56)

Частота колебаний (в герцах) выражает число колебаний (периодов), совершаемое системой в одну секунду.

Выражение   в уравнении (54) называют круговой частотой собственных колебаний, обозначаемое ω₀. Связь между круговой и собственной частотами незатухающих колебаний, периодом и параметрами системы можно установить на основании уравнения (56).

ω₀ = = 2π· f₀ = 2π / Т₀ . (57)

В большинстве приборов незатухающие колебания подвижной системы недопустимы, поскольку становится невозможным произвести отсчет показаний прибора.

Рассмотрим теперь собственные колебания системы, имеющей затухание, создаваемое успокоителем. Как в предыдущем случае моменты трения и моменты внешних сил считаем равными нулю. Тогда уравнение (52) примет вид:

J·d² α /dt² + c·dα /dt + K· α = 0.

разделив уравнение на J , получим:

d²α /dt² + (c / J) ·dα /dt + K·α / J = 0. (58)

В уравнении (58) согласно принятым ранее обозначениям:

K / J =

Введём ещё одно обозначение: β = c/(2· ) , где величина β называется степенью успокоения. Степень успокоения β и частота собственных колебаний ω₀ полностью определяют характер движения подвижной системы. Определим, чему равно произведение  β·ω₀:

β·ω₀  = (c/2· )· = c/(2J),

откуда

с = 2·J ·β·ω₀ и c / J = 2·β·ω₀. (59)

Тогда уравнение (58) может быть преобразовано к следующему виду:

d²α /dt² + 2·β·ω₀·dα /dt + ·α = 0. (60)

Решение уравнения (60) - закон изменения α во времени, т.е. вид функции α = f(t) зависит от величины степени успокоения β. В зависимости от условий (β <1, β = 1, β >1) решение уравнения (60) может иметь один из следующих трех видов.

При  β <1 решение уравнения (60) примет вид:

α = α₀ ·е^{- β·ω0·t}· [( β /  )· sin(ω₀· ·t) + cos(ω₀· ·t)]. (61)

Из уравнения следует, что система будет совершать колебательное движение. Но благодаря отрицательному показателю степени у основания е амплитуда колебаний будет с течением времени убывать, т.е. колебания будут затухающими (см. рис. 2).

При β = 1 решение уравнения (60) при принятых ранее начальных условиях будет:

α = α₀ ·е^{- β·ω0·t}·(1+ β·ω₀· t). (62)

Подвижная система в этом случае не совершает колебания, а плавно подходит к начальному положению (см. рис. 10, кривая 1). Такое движение называется апериодическим.

При β >1 характер движения остается апериодическим, но с более медленным приближением системы к положению равновесия (см. рис. 10, кривая 2).

Степень успокоения β = 1 является граничной между колебательным (β <1) и апериодическим (β >1) движениями подвижной системы. Поэтому режим успокоения колебаний при β = 1 называют режимом критического успокоения или просто критическим режимом.

Проанализируем полученные зависимости. Сравнивая уравнения (61) и (54) видим, что введение в систему успокоителя изменило частоту колебаний системы. Период затухающих колебаний системы при β <1 согласно уравнению (61) будет:

Т = 2π /( ω₀· ) (63)

или  

Т = Т₀ / . (64)

α

α₀

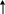t

Δα

Рис. 10

Отсюда видно, что период Т затухающих колебаний при наличии в системе успокоителя больше периода Т₀ собственных незатухающих колебаний, причем по мере приближения величины степени успокоения β к единице величина периода приближается к бесконечности, а движение к - апериодическому.

Время в течение, которого подвижная система устанавливается в положение равновесия, называют временем успокоения. При расчете времени успокоения чаще всего пользуются коэффициентом  λ, характеризующим относительную точность установки в положение равновесия. Если начальное отклонение равно  α₀, то:

λ = Δα / α₀.

При расчётах может возникнуть необходимость подобрать при заданных λ и Т₀ такую степень успокоения β_опт , чтобы время успокоения было минимальным. Для этого можно пользоваться формулой:

λ = π· β_опт ∕ . (65)

Приведённая формула даёт хорошие результаты для 0,7<β <1, когда подвижная система фактически делает не более одного полуколебания. Время успокоения можно определять по следующей формуле:

t_усп = Т₀∙(π – θ) / (2π· ), (66)

где: θ = arctg .

При апериодическом движении системы характерной величиной является время успокоения t_усп при заданной относительной точности установки λ. Так как увеличение степени успокоения сверх единицы приводит к увеличению времени затухания (см. рис. 10), то в приборах, где всегда стремятся сделать время затухания минимальным, степень успокоения β >1 обычно не применяют.