3. Конструювання та розрахунок вилки і підшипників жорстких карданних шарнірів нерівних кутових швидкостей.

4. В икористання поняття нормованої функції для визначення ймовірності заміни деталі та кількості замін деталі.

Под влиянием условий эксплуатации, квалификации персонала, неоднородности самих изделий и их начального состояния интенсивность и характер изменения параметра технического состояния у разных изделий (автомобилей) будет различной (рис. 2.2). Наработка на отказ будет случайной величиной и иметь вариацию (рис. 2.2а), неминуема также вариация технического состояния y_i на определённом пробеге l_o и как следствие — вариация трудоемкости и продолжительности выполнения работ по восстановлению технического состояния.

Рис. 2.2. Вариация ресурса (а) и технического состояния (б)

     Следовательно, т. к. наработка на отказ, трудоёмкость и продолжительность являются случайными величинами, важно знать характеристики случайной величины:

         — среднее значение

                                                            (2.4)

          — среднеквадратическое отклонение

                                                                                        (2.5)

          — коэффициент вариации

                                                                                                        (2.6)

Различают случайные величины:

         а) Малой вариацией .

         б) Средней вариацией .

         в) Большой вариацией .

    Вероятность — численная мера степени объективно существующей возможности появления изучаемого события.

                                                                                                    (2.7)

Если Р = 1 — событие достоверно; Р » 0 — событие маловероятно.

    Вероятность безотказной работы R(x) — отношение числа безотказной работы изделия за наработку Х к общему числу случаев.

                                                                        (2.8)

где m(x) — число отказавших изделий к моменту наработки Х.

    Вероятность отказа F(x) — событие противоположное вероятности безотказной работы:

                                                                                (2.9)

    Плотность вероятности отказа f(x) — вероятность отказа за малую единицу времени при работе узла, агрегата, деталей без замены.

Если , то при n = const дифференцируя, получим:

                                                                                            (2.12)

где          — элементарная вероятность, с которой в любой момент времени происходят отказы при работе детали, агрегата без замены.

    Если эту величину отнести к общему числу деталей, то получим плотность вероятности отказа.

                                                                                            (2.13)

учитывая, что     ,     получим:

                                                                                                (2.14)

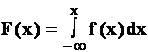
F(x) — называется интегральной функцией распределения.

f(x)— называется дифференциальной функцией распределения.

Рис. 2.3 Интегральная и дифференциальная функции распределения

Так как     ,     то     .

Имея значения F(x) или f(x), можно произвести оценку надежности данного изделия, т. е. определить вероятности отказа и безотказной работы и среднюю наработку до отказа:

                                                                                            (2.15)

    Дифференциальная функция распределения f(x) иногда называется законом распределения случайной величины.

    Различают несколько законов распределения случайной величины, например, нормальный закон, логарифмически — нормальный закон, закон Вейбулла-Гнеденко и т. д.

    Нормальный закон — когда на протекание исследуемого процесса и его результат влияет сравнительно большое число независимых (или слабозависимых) факторов, каждый из которых, в отдельности, оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных. Плотность вероятности распределения параметра при нормальном законе определяется по формуле

                                                                                (2.16)

тогда вероятность безотказной работы R(x) и вероятность отказа F(x) определяются:

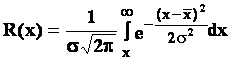                                                                           (2.17)

    При расчетах часто пользуются понятием нормированной функции Ф(z), для которой принимается новая случайная величина — нормированное отклонение см. :

                                                                                                    (2.18)

 при          значение нормированной функции Ф(z) принимает вид

                                                (2.19)

Задача. Определить вероятность первой замены при пробеге 70 тыс. км. от начала эксплуатации, при 95 тыс. км. и  30 тыс. км.

Решение:

,

смотри 

  .

 Таким образом, примерно 20% АТС потребуют ремонта при пробеге 70 тыс. км.

.